Policy Optimization finds Nash Equilibrium in Regularized General-Sum LQ Games

In this paper, we investigate the impact of introducing relative entropy regularization on the Nash Equilibria (NE) of General-Sum $N$-agent games, revealing the fact that the NE of such games conform to linear Gaussian policies. Moreover, it delineates sufficient conditions, contingent upon the adequacy of entropy regularization, for the uniqueness of the NE within the game. As Policy Optimization serves as a foundational approach for Reinforcement Learning (RL) techniques aimed at finding the NE, in this work we prove the linear convergence of a policy optimization algorithm which (subject to the adequacy of entropy regularization) is capable of provably attaining the NE. Furthermore, in scenarios where the entropy regularization proves insufficient, we present a $\delta$-augmentation technique, which facilitates the achievement of an $\epsilon$-NE within the game.

Independent RL for Cooperative-Competitive Agents: A Mean-Field Perspective

We address in this paper Reinforcement Learning (RL) among agents that are grouped into teams such that there is cooperation within each team but general-sum (non-zero sum) competition across different teams. To develop an RL method that provably achieves a Nash equilibrium, we focus on a linear-quadratic structure. Moreover, to tackle the non-stationarity induced by multi-agent interactions in the finite population setting, we consider the case where the number of agents within each team is infinite, i.e., the mean-field setting. This results in a General-Sum LQ Mean-Field Type Game (GS-MFTGs). We characterize the Nash equilibrium (NE) of the GS-MFTG, under a standard invertibility condition. This MFTG NE is then shown to be $\mathcal{O}(1/M)$-NE for the finite population game where $M$ is a lower bound on the number of agents in each team. These structural results motivate an algorithm called Multi-player Receding-horizon Natural Policy Gradient (MRPG), where each team minimizes its cumulative cost independently in a receding-horizon manner. Despite the non-convexity of the problem, we establish that the resulting algorithm converges to a global NE through a novel problem decomposition into sub-problems using backward recursive discrete-time Hamilton-Jacobi-Isaacs (HJI) equations, in which independent natural policy gradient is shown to exhibit linear convergence under time-independent diagonal dominance. Experiments illuminate the merits of this approach in practice.

Oracle-free Reinforcement Learning in Mean-Field Games along a Single Sample Path

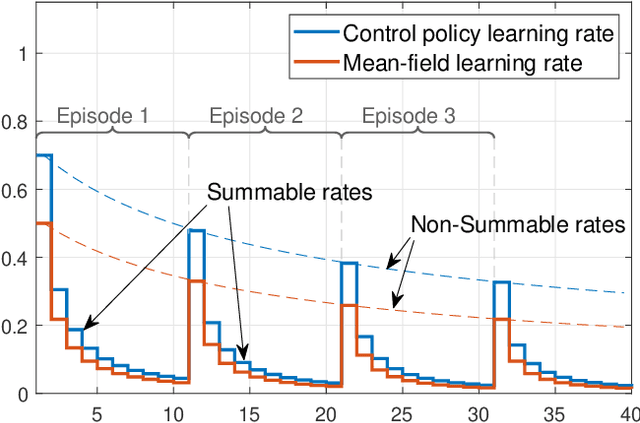
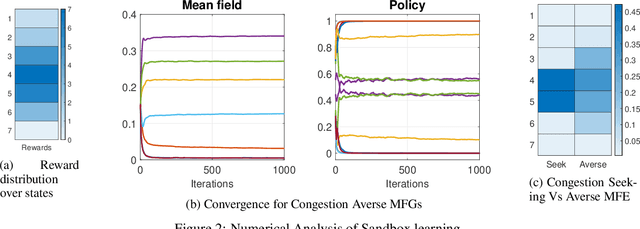
We consider online reinforcement learning in Mean-Field Games. In contrast to the existing works, we alleviate the need for a mean-field oracle by developing an algorithm that estimates the mean-field and the optimal policy using a single sample path of the generic agent. We call this Sandbox Learning, as it can be used as a warm-start for any agent operating in a multi-agent non-cooperative setting. We adopt a two timescale approach in which an online fixed-point recursion for the mean-field operates on a slower timescale and in tandem with a control policy update on a faster timescale for the generic agent. Under a sufficient exploration condition, we provide finite sample convergence guarantees in terms of convergence of the mean-field and control policy to the mean-field equilibrium. The sample complexity of the Sandbox learning algorithm is $\mathcal{O}(\epsilon^{-4})$. Finally, we empirically demonstrate effectiveness of the sandbox learning algorithm in a congestion game.

Reinforcement Learning in Non-Stationary Discrete-Time Linear-Quadratic Mean-Field Games

In this paper, we study large population multi-agent reinforcement learning (RL) in the context of discrete-time linear-quadratic mean-field games (LQ-MFGs). Our setting differs from most existing work on RL for MFGs, in that we consider a non-stationary MFG over an infinite horizon. We propose an actor-critic algorithm to iteratively compute the mean-field equilibrium (MFE) of the LQ-MFG. There are two primary challenges: i) the non-stationarity of the MFG induces a linear-quadratic tracking problem, which requires solving a backwards-in-time (non-causal) equation that cannot be solved by standard (causal) RL algorithms; ii) Many RL algorithms assume that the states are sampled from the stationary distribution of a Markov chain (MC), that is, the chain is already mixed, an assumption that is not satisfied for real data sources. We first identify that the mean-field trajectory follows linear dynamics, allowing the problem to be reformulated as a linear quadratic Gaussian problem. Under this reformulation, we propose an actor-critic algorithm that allows samples to be drawn from an unmixed MC. Finite-sample convergence guarantees for the algorithm are then provided. To characterize the performance of our algorithm in multi-agent RL, we have developed an error bound with respect to the Nash equilibrium of the finite-population game.

Multi-agent Planning for thermalling gliders using multi level graph-search

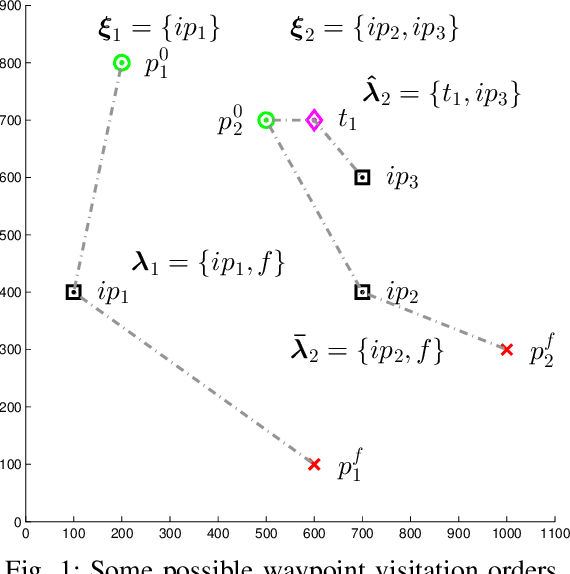
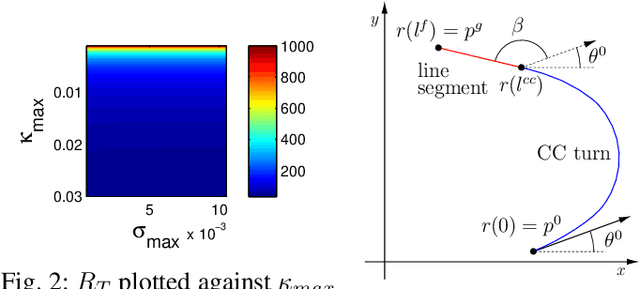
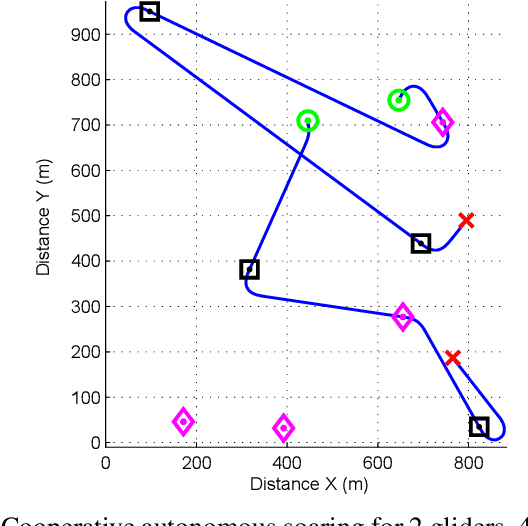
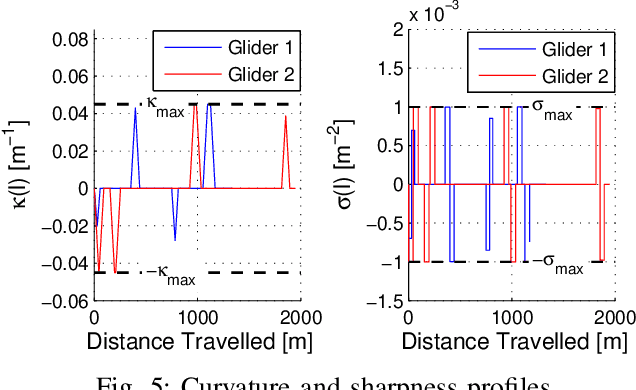
This paper solves a path planning problem for a group of gliders. The gliders are tasked with visiting a set of interest points. The gliders have limited range but are able to increase their range by visiting special points called thermals. The problem addressed in this paper is of path planning for the gliders such that, the total number of interest points visited by the gliders is maximized. This is referred to as the multi-agent problem. The problem is solved by first decomposing it into several single-agent problems. In a single-agent problem a set of interest points are allocated to a single glider. This problem is solved by planning a path which maximizes the number of visited interest points from the allocated set. This is achieved through a uniform cost graph search, as shown in our earlier work. The multi-agent problem now consists of determining the best allocation (of interest points) for each glider. Two ways are presented of solving this problem, a brute force search approach as shown in earlier work and a Branch\&Bound type graph search. The Branch&Bound approach is the main contribution of the paper. This approach is proven to be optimal and shown to be faster than the brute force search using simulations.