Aamer Iqbal Bhatti
Multi-agent Planning for thermalling gliders using multi level graph-search
Jul 02, 2020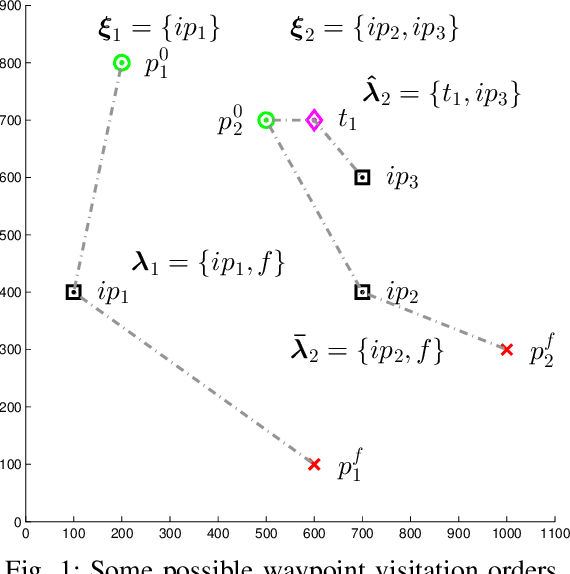
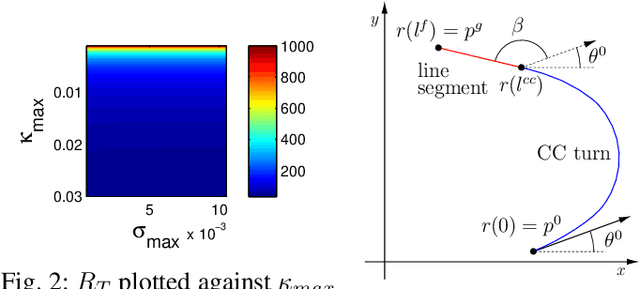
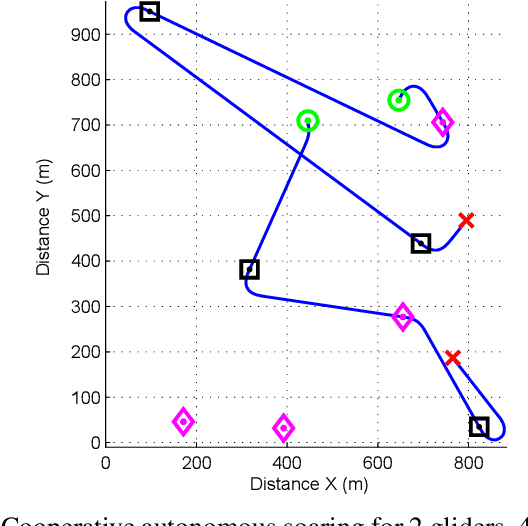
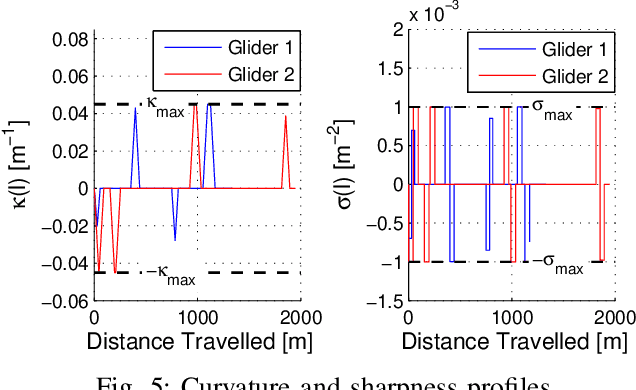
Abstract:This paper solves a path planning problem for a group of gliders. The gliders are tasked with visiting a set of interest points. The gliders have limited range but are able to increase their range by visiting special points called thermals. The problem addressed in this paper is of path planning for the gliders such that, the total number of interest points visited by the gliders is maximized. This is referred to as the multi-agent problem. The problem is solved by first decomposing it into several single-agent problems. In a single-agent problem a set of interest points are allocated to a single glider. This problem is solved by planning a path which maximizes the number of visited interest points from the allocated set. This is achieved through a uniform cost graph search, as shown in our earlier work. The multi-agent problem now consists of determining the best allocation (of interest points) for each glider. Two ways are presented of solving this problem, a brute force search approach as shown in earlier work and a Branch\&Bound type graph search. The Branch&Bound approach is the main contribution of the paper. This approach is proven to be optimal and shown to be faster than the brute force search using simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge