Oracle-free Reinforcement Learning in Mean-Field Games along a Single Sample Path
Paper and Code
Aug 26, 2022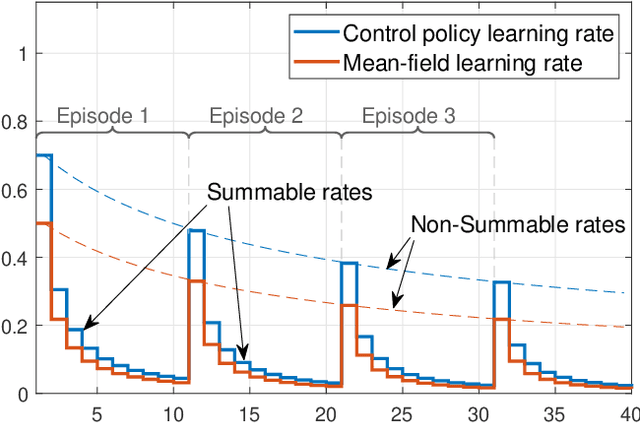
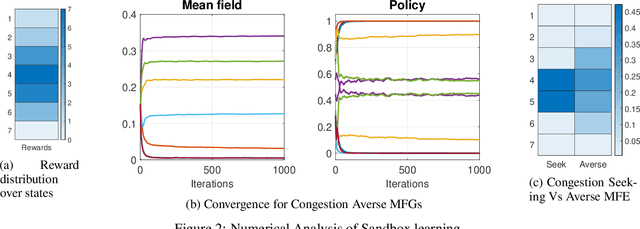
We consider online reinforcement learning in Mean-Field Games. In contrast to the existing works, we alleviate the need for a mean-field oracle by developing an algorithm that estimates the mean-field and the optimal policy using a single sample path of the generic agent. We call this Sandbox Learning, as it can be used as a warm-start for any agent operating in a multi-agent non-cooperative setting. We adopt a two timescale approach in which an online fixed-point recursion for the mean-field operates on a slower timescale and in tandem with a control policy update on a faster timescale for the generic agent. Under a sufficient exploration condition, we provide finite sample convergence guarantees in terms of convergence of the mean-field and control policy to the mean-field equilibrium. The sample complexity of the Sandbox learning algorithm is $\mathcal{O}(\epsilon^{-4})$. Finally, we empirically demonstrate effectiveness of the sandbox learning algorithm in a congestion game.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge