Interacting Large Language Model Agents. Interpretable Models and Social Learning

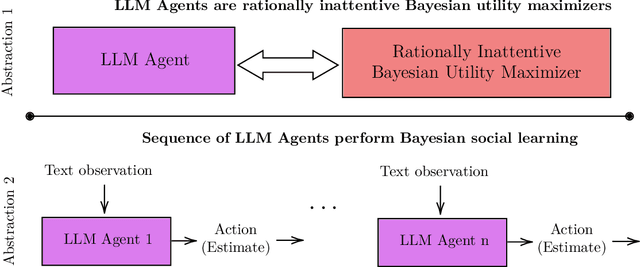
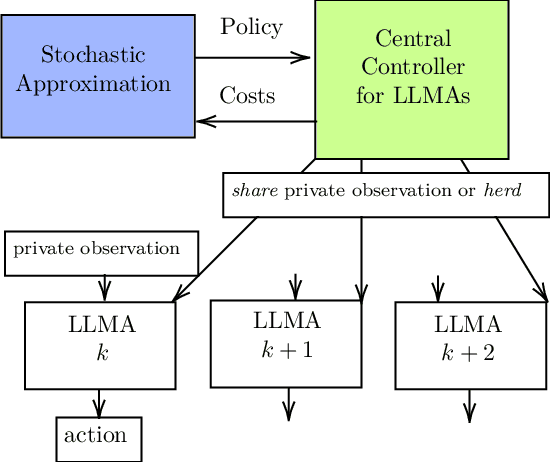
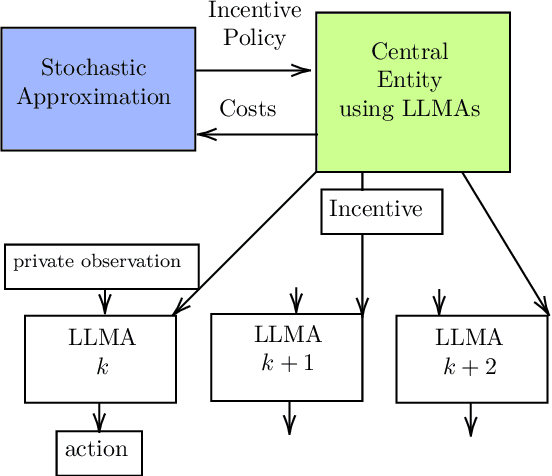
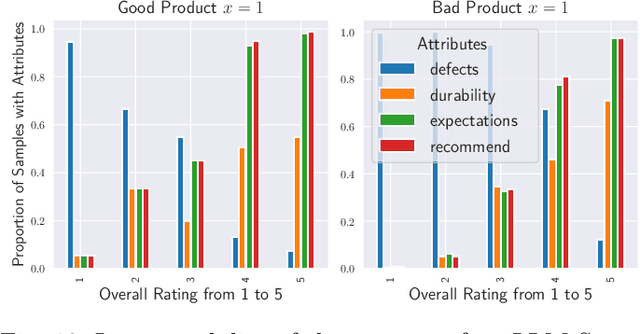
This paper develops theory and algorithms for interacting large language model agents (LLMAs) using methods from statistical signal processing and microeconomics. While both fields are mature, their application to decision-making by interacting LLMAs remains unexplored. Motivated by Bayesian sentiment analysis on online platforms, we construct interpretable models and stochastic control algorithms that enable LLMAs to interact and perform Bayesian inference. Because interacting LLMAs learn from prior decisions and external inputs, they exhibit bias and herding behavior. Thus, developing interpretable models and stochastic control algorithms is essential to understand and mitigate these behaviors. This paper has three main results. First, we show using Bayesian revealed preferences from microeconomics that an individual LLMA satisfies the sufficient conditions for rationally inattentive (bounded rationality) utility maximization and, given an observation, the LLMA chooses an action that maximizes a regularized utility. Second, we utilize Bayesian social learning to construct interpretable models for LLMAs that interact sequentially with each other and the environment while performing Bayesian inference. Our models capture the herding behavior exhibited by interacting LLMAs. Third, we propose a stochastic control framework to delay herding and improve state estimation accuracy under two settings: (a) centrally controlled LLMAs and (b) autonomous LLMAs with incentives. Throughout the paper, we demonstrate the efficacy of our methods on real datasets for hate speech classification and product quality assessment, using open-source models like Mistral and closed-source models like ChatGPT. The main takeaway of this paper, based on substantial empirical analysis and mathematical formalism, is that LLMAs act as rationally bounded Bayesian agents that exhibit social learning when interacting.

Annotation Efficiency: Identifying Hard Samples via Blocked Sparse Linear Bandits

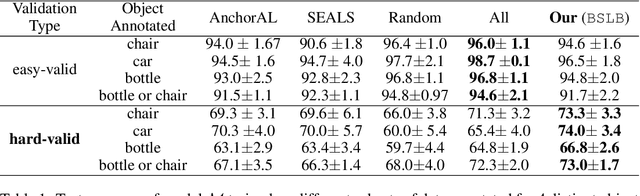
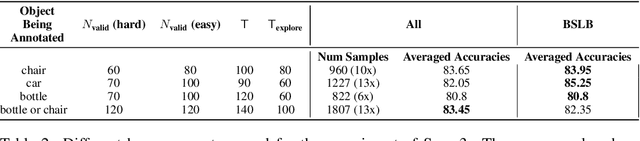
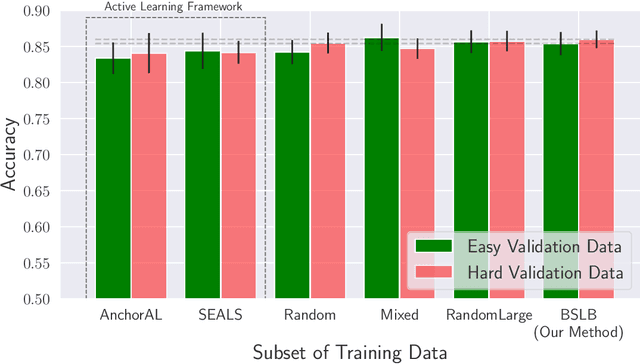
This paper considers the problem of annotating datapoints using an expert with only a few annotation rounds in a label-scarce setting. We propose soliciting reliable feedback on difficulty in annotating a datapoint from the expert in addition to ground truth label. Existing literature in active learning or coreset selection turns out to be less relevant to our setting since they presume the existence of a reliable trained model, which is absent in the label-scarce regime. However, the literature on coreset selection emphasizes the presence of difficult data points in the training set to perform supervised learning in downstream tasks (Mindermann et al., 2022). Therefore, for a given fixed annotation budget of $\mathsf{T}$ rounds, we model the sequential decision-making problem of which (difficult) datapoints to choose for annotation in a sparse linear bandits framework with the constraint that no arm can be pulled more than once (blocking constraint). With mild assumptions on the datapoints, our (computationally efficient) Explore-Then-Commit algorithm BSLB achieves a regret guarantee of $\widetilde{\mathsf{O}}(k^{\frac{1}{3}} \mathsf{T}^{\frac{2}{3}} +k^{-\frac{1}{2}} \beta_k + k^{-\frac{1}{12}} \beta_k^{\frac{1}{2}}\mathsf{T}^{\frac{5}{6}})$ where the unknown parameter vector has tail magnitude $\beta_k$ at sparsity level $k$. To this end, we show offline statistical guarantees of Lasso estimator with mild Restricted Eigenvalue (RE) condition that is also robust to sparsity. Finally, we propose a meta-algorithm C-BSLB that does not need knowledge of the optimal sparsity parameters at a no-regret cost. We demonstrate the efficacy of our BSLB algorithm for annotation in the label-scarce setting for an image classification task on the PASCAL-VOC dataset, where we use real-world annotation difficulty scores.

Slow Convergence of Interacting Kalman Filters in Word-of-Mouth Social Learning

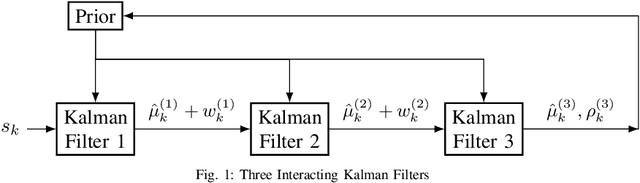
We consider word-of-mouth social learning involving $m$ Kalman filter agents that operate sequentially. The first Kalman filter receives the raw observations, while each subsequent Kalman filter receives a noisy measurement of the conditional mean of the previous Kalman filter. The prior is updated by the $m$-th Kalman filter. When $m=2$, and the observations are noisy measurements of a Gaussian random variable, the covariance goes to zero as $k^{-1/3}$ for $k$ observations, instead of $O(k^{-1})$ in the standard Kalman filter. In this paper we prove that for $m$ agents, the covariance decreases to zero as $k^{-(2^m-1)}$, i.e, the learning slows down exponentially with the number of agents. We also show that by artificially weighing the prior at each time, the learning rate can be made optimal as $k^{-1}$. The implication is that in word-of-mouth social learning, artificially re-weighing the prior can yield the optimal learning rate.

Finite Sample and Large Deviations Analysis of Stochastic Gradient Algorithm with Correlated Noise

We analyze the finite sample regret of a decreasing step size stochastic gradient algorithm. We assume correlated noise and use a perturbed Lyapunov function as a systematic approach for the analysis. Finally we analyze the escape time of the iterates using large deviations theory.

Distributionally Robust Inverse Reinforcement Learning for Identifying Multi-Agent Coordinated Sensing

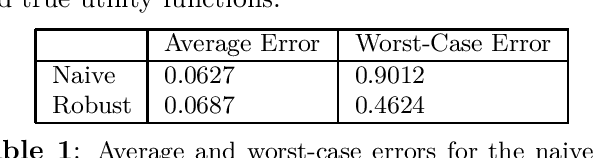
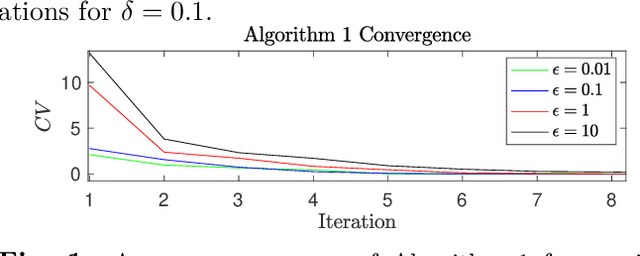
We derive a minimax distributionally robust inverse reinforcement learning (IRL) algorithm to reconstruct the utility functions of a multi-agent sensing system. Specifically, we construct utility estimators which minimize the worst-case prediction error over a Wasserstein ambiguity set centered at noisy signal observations. We prove the equivalence between this robust estimation and a semi-infinite optimization reformulation, and we propose a consistent algorithm to compute solutions. We illustrate the efficacy of this robust IRL scheme in numerical studies to reconstruct the utility functions of a cognitive radar network from observed tracking signals.

Identifying Hate Speech Peddlers in Online Platforms. A Bayesian Social Learning Approach for Large Language Model Driven Decision-Makers

This paper studies the problem of autonomous agents performing Bayesian social learning for sequential detection when the observations of the state belong to a high-dimensional space and are expensive to analyze. Specifically, when the observations are textual, the Bayesian agent can use a large language model (LLM) as a map to get a low-dimensional private observation. The agent performs Bayesian learning and takes an action that minimizes the expected cost and is visible to subsequent agents. We prove that a sequence of such Bayesian agents herd in finite time to the public belief and take the same action disregarding the private observations. We propose a stopping time formulation for quickest time herding in social learning and optimally balance privacy and herding. Structural results are shown on the threshold nature of the optimal policy to the stopping time problem. We illustrate the application of our framework when autonomous Bayesian detectors aim to sequentially identify if a user is a hate speech peddler on an online platform by parsing text observations using an LLM. We numerically validate our results on real-world hate speech datasets. We show that autonomous Bayesian agents designed to flag hate speech peddlers in online platforms herd and misclassify the users when the public prior is strong. We also numerically show the effect of a threshold policy in delaying herding.

Structured Reinforcement Learning for Incentivized Stochastic Covert Optimization

This paper studies how a stochastic gradient algorithm (SG) can be controlled to hide the estimate of the local stationary point from an eavesdropper. Such problems are of significant interest in distributed optimization settings like federated learning and inventory management. A learner queries a stochastic oracle and incentivizes the oracle to obtain noisy gradient measurements and perform SG. The oracle probabilistically returns either a noisy gradient of the function} or a non-informative measurement, depending on the oracle state and incentive. The learner's query and incentive are visible to an eavesdropper who wishes to estimate the stationary point. This paper formulates the problem of the learner performing covert optimization by dynamically incentivizing the stochastic oracle and obfuscating the eavesdropper as a finite-horizon Markov decision process (MDP). Using conditions for interval-dominance on the cost and transition probability structure, we show that the optimal policy for the MDP has a monotone threshold structure. We propose searching for the optimal stationary policy with the threshold structure using a stochastic approximation algorithm and a multi-armed bandit approach. The effectiveness of our methods is numerically demonstrated on a covert federated learning hate-speech classification task.

Controlling Federated Learning for Covertness

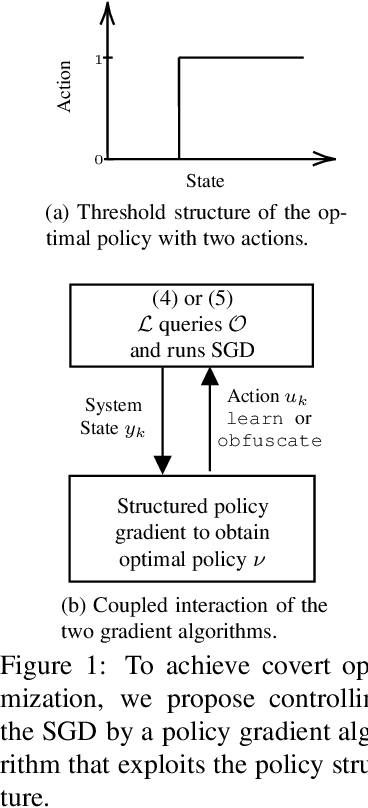
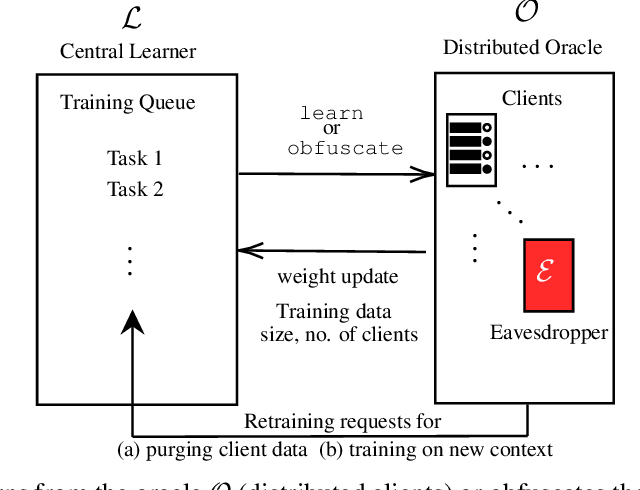
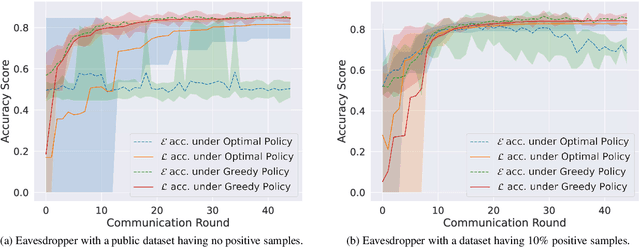
A learner aims to minimize a function $f$ by repeatedly querying a distributed oracle that provides noisy gradient evaluations. At the same time, the learner seeks to hide $\arg\min f$ from a malicious eavesdropper that observes the learner's queries. This paper considers the problem of \textit{covert} or \textit{learner-private} optimization, where the learner has to dynamically choose between learning and obfuscation by exploiting the stochasticity. The problem of controlling the stochastic gradient algorithm for covert optimization is modeled as a Markov decision process, and we show that the dynamic programming operator has a supermodular structure implying that the optimal policy has a monotone threshold structure. A computationally efficient policy gradient algorithm is proposed to search for the optimal querying policy without knowledge of the transition probabilities. As a practical application, our methods are demonstrated on a hate speech classification task in a federated setting where an eavesdropper can use the optimal weights to generate toxic content, which is more easily misclassified. Numerical results show that when the learner uses the optimal policy, an eavesdropper can only achieve a validation accuracy of $52\%$ with no information and $69\%$ when it has a public dataset with 10\% positive samples compared to $83\%$ when the learner employs a greedy policy.

Fréchet Statistics Based Change Point Detection in Multivariate Hawkes Process

This paper proposes a new approach for change point detection in causal networks of multivariate Hawkes processes using Frechet statistics. Our method splits the point process into overlapping windows, estimates kernel matrices in each window, and reconstructs the signed Laplacians by treating the kernel matrices as the adjacency matrices of the causal network. We demonstrate the effectiveness of our method through experiments on both simulated and real-world cryptocurrency datasets. Our results show that our method is capable of accurately detecting and characterizing changes in the causal structure of multivariate Hawkes processes, and may have potential applications in fields such as finance and neuroscience. The proposed method is an extension of previous work on Frechet statistics in point process settings and represents an important contribution to the field of change point detection in multivariate point processes.

Energy-Efficient Mining for Blockchain-Enabled IoT Applications. An Optimal Multiple-Stopping Time Approach

What are the optimal times for an Internet of Things (IoT) device to act as a blockchain miner? The aim is to minimize the energy consumed by low-power IoT devices that log their data into a secure (tamper-proof) distributed ledger. We formulate the energy-efficient blockchain mining for IoT devices as a multiple-stopping time partially observed Markov decision process (POMDP) to maximize the probability of adding a block in the blockchain; we also present a model to optimize the number of stops (mining instants). In general, POMDPs are computationally intractable to solve, but we show mathematically using submodularity that the optimal mining policy has a useful structure: 1) it is monotone in belief space, and 2) it exhibits a threshold structure, which divides the belief space into two connected sets. Exploiting the structural results, we formulate a computationally-efficient linear mining policy for the blockchain-enabled IoT device. We present a policy gradient technique to optimize the parameters of the linear mining policy. Finally, we use synthetic and real Bitcoin datasets to study the performance of our proposed mining policy. We demonstrate the energy efficiency achieved by the optimal linear mining policy in contrast to other heuristic strategies.