Distributionally Robust Inverse Reinforcement Learning for Identifying Multi-Agent Coordinated Sensing
Paper and Code
Sep 22, 2024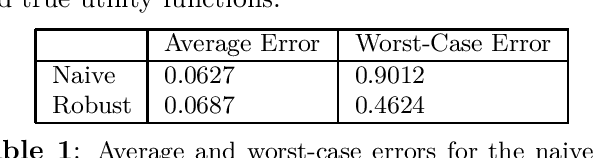
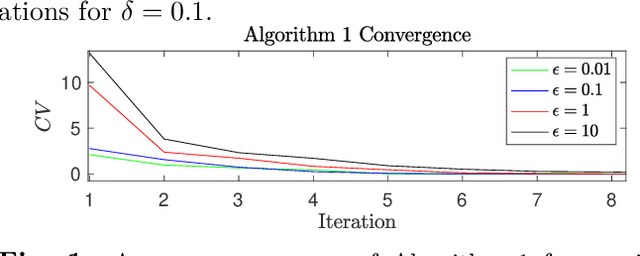
We derive a minimax distributionally robust inverse reinforcement learning (IRL) algorithm to reconstruct the utility functions of a multi-agent sensing system. Specifically, we construct utility estimators which minimize the worst-case prediction error over a Wasserstein ambiguity set centered at noisy signal observations. We prove the equivalence between this robust estimation and a semi-infinite optimization reformulation, and we propose a consistent algorithm to compute solutions. We illustrate the efficacy of this robust IRL scheme in numerical studies to reconstruct the utility functions of a cognitive radar network from observed tracking signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge