Distributionally Robust Inverse Reinforcement Learning for Identifying Multi-Agent Coordinated Sensing

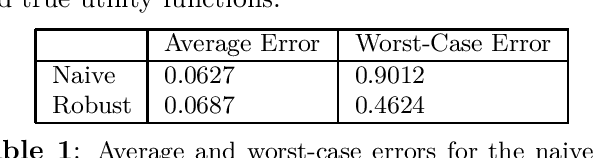
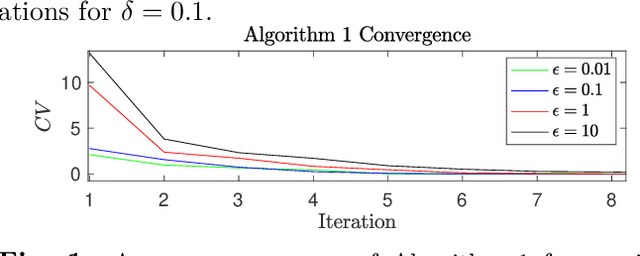
We derive a minimax distributionally robust inverse reinforcement learning (IRL) algorithm to reconstruct the utility functions of a multi-agent sensing system. Specifically, we construct utility estimators which minimize the worst-case prediction error over a Wasserstein ambiguity set centered at noisy signal observations. We prove the equivalence between this robust estimation and a semi-infinite optimization reformulation, and we propose a consistent algorithm to compute solutions. We illustrate the efficacy of this robust IRL scheme in numerical studies to reconstruct the utility functions of a cognitive radar network from observed tracking signals.

Finite-Sample Bounds for Adaptive Inverse Reinforcement Learning using Passive Langevin Dynamics

Stochastic gradient Langevin dynamics (SGLD) are a useful methodology for sampling from probability distributions. This paper provides a finite sample analysis of a passive stochastic gradient Langevin dynamics algorithm (PSGLD) designed to achieve inverse reinforcement learning. By "passive", we mean that the noisy gradients available to the PSGLD algorithm (inverse learning process) are evaluated at randomly chosen points by an external stochastic gradient algorithm (forward learner). The PSGLD algorithm thus acts as a randomized sampler which recovers the cost function being optimized by this external process. Previous work has analyzed the asymptotic performance of this passive algorithm using stochastic approximation techniques; in this work we analyze the non-asymptotic performance. Specifically, we provide finite-time bounds on the 2-Wasserstein distance between the passive algorithm and its stationary measure, from which the reconstructed cost function is obtained.

Statistical Detection of Coordination in a Cognitive Radar Network through Inverse Multi-objective Optimization

Consider a target being tracked by a cognitive radar network. If the target can intercept noisy radar emissions, how can it detect coordination in the radar network? By 'coordination' we mean that the radar emissions satisfy Pareto optimality with respect to multi-objective optimization over the objective functions of each radar and a constraint on total network power output. This paper provides a novel inverse multi-objective optimization approach for statistically detecting Pareto optimal ('coordinating') behavior, from a finite dataset of noisy radar emissions. Specifically, we develop necessary and sufficient conditions for radar network emissions to be consistent with multi-objective optimization (coordination), and we provide a statistical detector with theoretical guarantees for determining this consistency when radar emissions are observed in noise. We also provide numerical simulations which validate our approach. Note that while we make use of the specific framework of a radar network coordination problem, our results apply more generally to the field of inverse multi-objective optimization.

Identifying Coordination in a Cognitive Radar Network -- A Multi-Objective Inverse Reinforcement Learning Approach

Consider a target being tracked by a cognitive radar network. If the target can intercept some radar network emissions, how can it detect coordination among the radars? By 'coordination' we mean that the radar emissions satisfy Pareto optimality with respect to multi-objective optimization over each radar's utility. This paper provides a novel multi-objective inverse reinforcement learning approach which allows for both detection of such Pareto optimal ('coordinating') behavior and subsequent reconstruction of each radar's utility function, given a finite dataset of radar network emissions. The method for accomplishing this is derived from the micro-economic setting of Revealed Preferences, and also applies to more general problems of inverse detection and learning of multi-objective optimizing systems.

Quickest Detection for Human-Sensor Systems using Quantum Decision Theory

In mathematical psychology, recent models for human decision-making use Quantum Decision Theory to capture important human-centric features such as order effects and violation of the sure-thing principle (total probability law). We construct and analyze a human-sensor system where a quickest detector aims to detect a change in an underlying state by observing human decisions that are influenced by the state. Apart from providing an analytical framework for such human-sensor systems, we also analyze the structure of the quickest detection policy. We show that the quickest detection policy has a single threshold and the optimal cost incurred is lower bounded by that of the classical quickest detector. This indicates that intermediate human decisions strictly hinder detection performance. We also analyze the sensitivity of the quickest detection cost with respect to the quantum decision parameters of the human decision maker, revealing that the performance is robust to inaccurate knowledge of the decision-making process. Numerical results are provided which suggest that observing the decisions of more rational decision makers will improve the quickest detection performance. Finally, we illustrate a numerical implementation of this quickest detector in the context of the Prisoner's Dilemma problem, in which it has been observed that Quantum Decision Theory can uniquely model empirically tested violations of the sure-thing principle.