Slow Convergence of Interacting Kalman Filters in Word-of-Mouth Social Learning
Paper and Code
Oct 11, 2024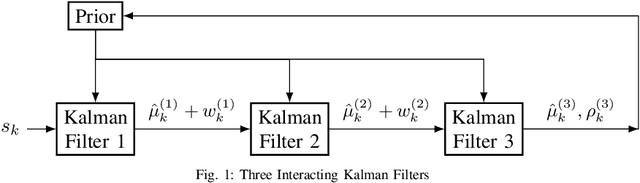
We consider word-of-mouth social learning involving $m$ Kalman filter agents that operate sequentially. The first Kalman filter receives the raw observations, while each subsequent Kalman filter receives a noisy measurement of the conditional mean of the previous Kalman filter. The prior is updated by the $m$-th Kalman filter. When $m=2$, and the observations are noisy measurements of a Gaussian random variable, the covariance goes to zero as $k^{-1/3}$ for $k$ observations, instead of $O(k^{-1})$ in the standard Kalman filter. In this paper we prove that for $m$ agents, the covariance decreases to zero as $k^{-(2^m-1)}$, i.e, the learning slows down exponentially with the number of agents. We also show that by artificially weighing the prior at each time, the learning rate can be made optimal as $k^{-1}$. The implication is that in word-of-mouth social learning, artificially re-weighing the prior can yield the optimal learning rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge