Finite Sample and Large Deviations Analysis of Stochastic Gradient Algorithm with Correlated Noise

We analyze the finite sample regret of a decreasing step size stochastic gradient algorithm. We assume correlated noise and use a perturbed Lyapunov function as a systematic approach for the analysis. Finally we analyze the escape time of the iterates using large deviations theory.

Kitchen Food Waste Image Segmentation and Classification for Compost Nutrients Estimation

The escalating global concern over extensive food wastage necessitates innovative solutions to foster a net-zero lifestyle and reduce emissions. The LILA home composter presents a convenient means of recycling kitchen scraps and daily food waste into nutrient-rich, high-quality compost. To capture the nutritional information of the produced compost, we have created and annotated a large high-resolution image dataset of kitchen food waste with segmentation masks of 19 nutrition-rich categories. Leveraging this dataset, we benchmarked four state-of-the-art semantic segmentation models on food waste segmentation, contributing to the assessment of compost quality of Nitrogen, Phosphorus, or Potassium. The experiments demonstrate promising results of using segmentation models to discern food waste produced in our daily lives. Based on the experiments, SegFormer, utilizing MIT-B5 backbone, yields the best performance with a mean Intersection over Union (mIoU) of 67.09. Class-based results are also provided to facilitate further analysis of different food waste classes.

Adaptive Non-reversible Stochastic Gradient Langevin Dynamics

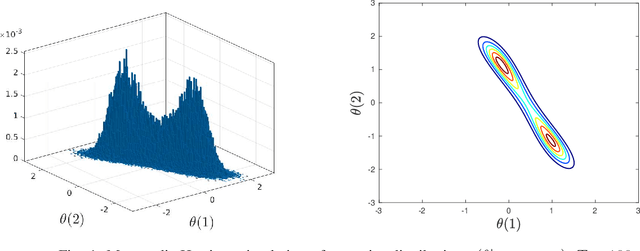
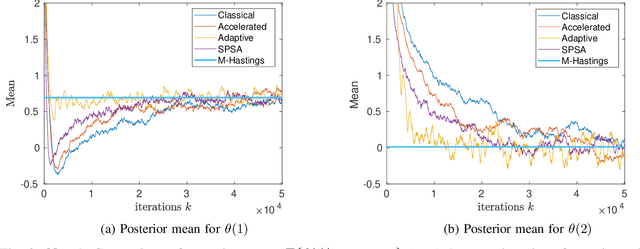
It is well known that adding any skew symmetric matrix to the gradient of Langevin dynamics algorithm results in a non-reversible diffusion with improved convergence rate. This paper presents a gradient algorithm to adaptively optimize the choice of the skew symmetric matrix. The resulting algorithm involves a non-reversible diffusion algorithm cross coupled with a stochastic gradient algorithm that adapts the skew symmetric matrix. The algorithm uses the same data as the classical Langevin algorithm. A weak convergence proof is given for the optimality of the choice of the skew symmetric matrix. The improved convergence rate of the algorithm is illustrated numerically in Bayesian learning and tracking examples.

Multi-kernel Passive Stochastic Gradient Algorithms

This paper develops a novel passive stochastic gradient algorithm. In passive stochastic approximation, the stochastic gradient algorithm does not have control over the location where noisy gradients of the cost function are evaluated. Classical passive stochastic gradient algorithms use a kernel that approximates a Dirac delta to weigh the gradients based on how far they are evaluated from the desired point. In this paper we construct a multi-kernel passive stochastic gradient algorithm. The algorithm performs substantially better in high dimensional problems and incorporates variance reduction. We analyze the weak convergence of the multi-kernel algorithm and its rate of convergence. In numerical examples, we study the multi-kernel version of the LMS algorithm to compare the performance with the classical passive version.

Langevin Dynamics for Inverse Reinforcement Learning of Stochastic Gradient Algorithms

Inverse reinforcement learning (IRL) aims to estimate the reward function of optimizing agents by observing their response (estimates or actions). This paper considers IRL when noisy estimates of the gradient of a reward function generated by multiple stochastic gradient agents are observed. We present a generalized Langevin dynamics algorithm to estimate the reward function $R(\theta)$; specifically, the resulting Langevin algorithm asymptotically generates samples from the distribution proportional to $\exp(R(\theta))$. The proposed IRL algorithms use kernel-based passive learning schemes. We also construct multi-kernel passive Langevin algorithms for IRL which are suitable for high dimensional data. The performance of the proposed IRL algorithms are illustrated on examples in adaptive Bayesian learning, logistic regression (high dimensional problem) and constrained Markov decision processes. We prove weak convergence of the proposed IRL algorithms using martingale averaging methods. We also analyze the tracking performance of the IRL algorithms in non-stationary environments where the utility function $R(\theta)$ jump changes over time as a slow Markov chain.