Adaptive Non-reversible Stochastic Gradient Langevin Dynamics

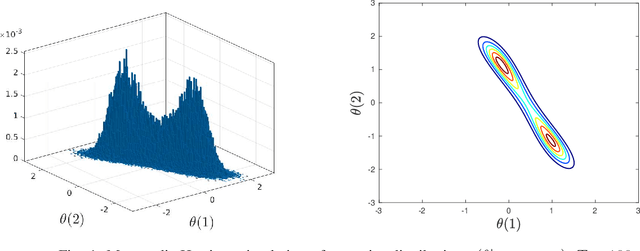
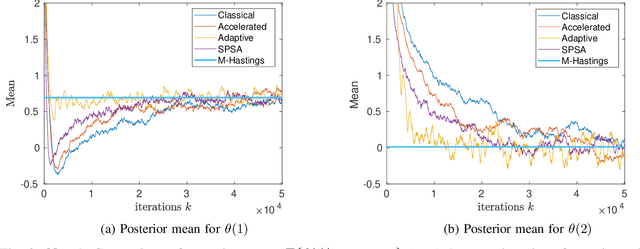
It is well known that adding any skew symmetric matrix to the gradient of Langevin dynamics algorithm results in a non-reversible diffusion with improved convergence rate. This paper presents a gradient algorithm to adaptively optimize the choice of the skew symmetric matrix. The resulting algorithm involves a non-reversible diffusion algorithm cross coupled with a stochastic gradient algorithm that adapts the skew symmetric matrix. The algorithm uses the same data as the classical Langevin algorithm. A weak convergence proof is given for the optimality of the choice of the skew symmetric matrix. The improved convergence rate of the algorithm is illustrated numerically in Bayesian learning and tracking examples.