Controlling Federated Learning for Covertness
Paper and Code
Aug 17, 2023
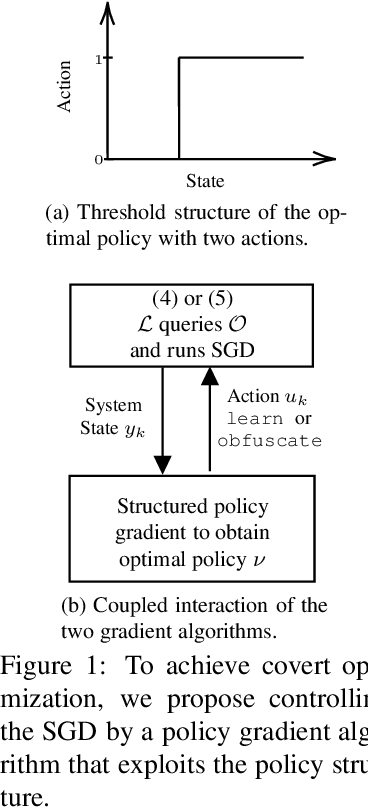
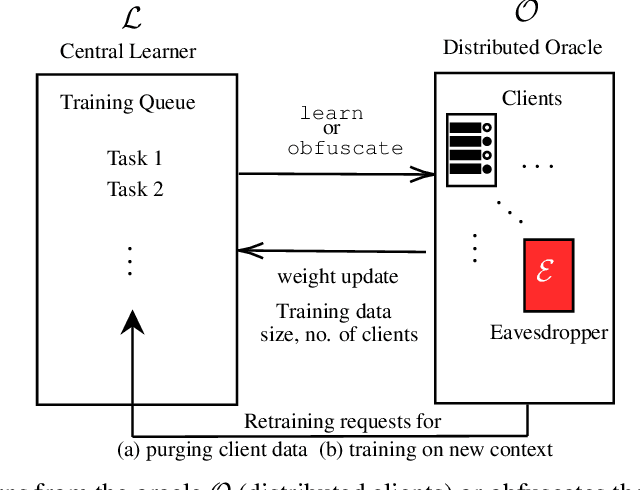
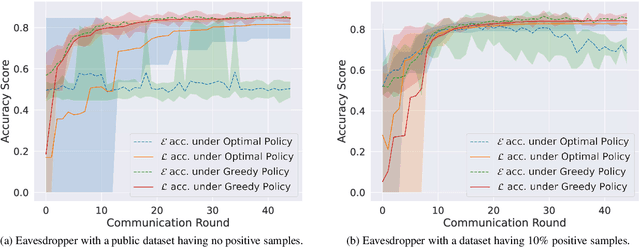
A learner aims to minimize a function $f$ by repeatedly querying a distributed oracle that provides noisy gradient evaluations. At the same time, the learner seeks to hide $\arg\min f$ from a malicious eavesdropper that observes the learner's queries. This paper considers the problem of \textit{covert} or \textit{learner-private} optimization, where the learner has to dynamically choose between learning and obfuscation by exploiting the stochasticity. The problem of controlling the stochastic gradient algorithm for covert optimization is modeled as a Markov decision process, and we show that the dynamic programming operator has a supermodular structure implying that the optimal policy has a monotone threshold structure. A computationally efficient policy gradient algorithm is proposed to search for the optimal querying policy without knowledge of the transition probabilities. As a practical application, our methods are demonstrated on a hate speech classification task in a federated setting where an eavesdropper can use the optimal weights to generate toxic content, which is more easily misclassified. Numerical results show that when the learner uses the optimal policy, an eavesdropper can only achieve a validation accuracy of $52\%$ with no information and $69\%$ when it has a public dataset with 10\% positive samples compared to $83\%$ when the learner employs a greedy policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge