Empirical Risk Minimization for Losses without Variance

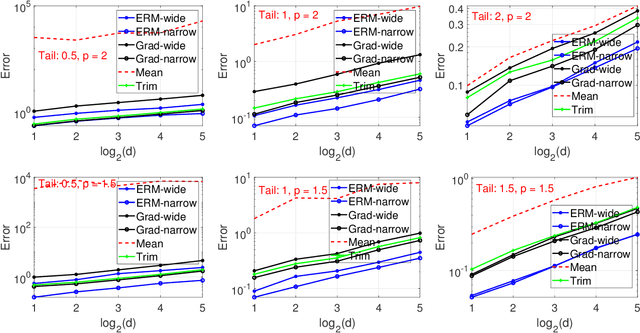
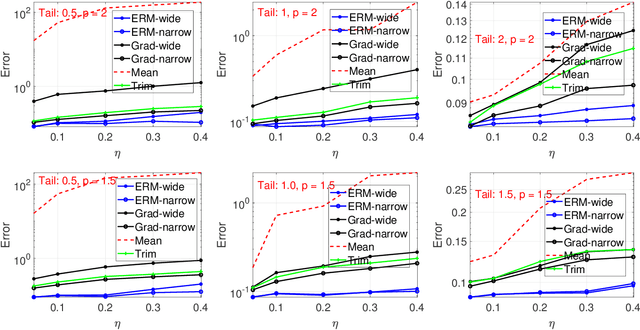
This paper considers an empirical risk minimization problem under heavy-tailed settings, where data does not have finite variance, but only has $p$-th moment with $p \in (1,2)$. Instead of using estimation procedure based on truncated observed data, we choose the optimizer by minimizing the risk value. Those risk values can be robustly estimated via using the remarkable Catoni's method (Catoni, 2012). Thanks to the structure of Catoni-type influence functions, we are able to establish excess risk upper bounds via using generalized generic chaining methods. Moreover, we take computational issues into consideration. We especially theoretically investigate two types of optimization methods, robust gradient descent algorithm and empirical risk-based methods. With an extensive numerical study, we find that the optimizer based on empirical risks via Catoni-style estimation indeed shows better performance than other baselines. It indicates that estimation directly based on truncated data may lead to unsatisfactory results.

Epsilon*: Privacy Metric for Machine Learning Models

We introduce Epsilon*, a new privacy metric for measuring the privacy risk of a single model instance prior to, during, or after deployment of privacy mitigation strategies. The metric does not require access to the training data sampling or model training algorithm. Epsilon* is a function of true positive and false positive rates in a hypothesis test used by an adversary in a membership inference attack. We distinguish between quantifying the privacy loss of a trained model instance and quantifying the privacy loss of the training mechanism which produces this model instance. Existing approaches in the privacy auditing literature provide lower bounds for the latter, while our metric provides a lower bound for the former by relying on an (${\epsilon}$,${\delta}$)-type of quantification of the privacy of the trained model instance. We establish a relationship between these lower bounds and show how to implement Epsilon* to avoid numerical and noise amplification instability. We further show in experiments on benchmark public data sets that Epsilon* is sensitive to privacy risk mitigation by training with differential privacy (DP), where the value of Epsilon* is reduced by up to 800% compared to the Epsilon* values of non-DP trained baseline models. This metric allows privacy auditors to be independent of model owners, and enables all decision-makers to visualize the privacy-utility landscape to make informed decisions regarding the trade-offs between model privacy and utility.

Adaptive Privacy Composition for Accuracy-first Mechanisms

In many practical applications of differential privacy, practitioners seek to provide the best privacy guarantees subject to a target level of accuracy. A recent line of work by \cite{LigettNeRoWaWu17, WhitehouseWuRaRo22} has developed such accuracy-first mechanisms by leveraging the idea of \emph{noise reduction} that adds correlated noise to the sufficient statistic in a private computation and produces a sequence of increasingly accurate answers. A major advantage of noise reduction mechanisms is that the analysts only pay the privacy cost of the least noisy or most accurate answer released. Despite this appealing property in isolation, there has not been a systematic study on how to use them in conjunction with other differentially private mechanisms. A fundamental challenge is that the privacy guarantee for noise reduction mechanisms is (necessarily) formulated as \emph{ex-post privacy} that bounds the privacy loss as a function of the released outcome. Furthermore, there has yet to be any study on how ex-post private mechanisms compose, which allows us to track the accumulated privacy over several mechanisms. We develop privacy filters \citep{RogersRoUlVa16, FeldmanZr21, WhitehouseRaRoWu22} that allow an analyst to adaptively switch between differentially private and ex-post private mechanisms subject to an overall privacy guarantee.

A Cover Time Study of a non-Markovian Algorithm

Given a traversal algorithm, cover time is the expected number of steps needed to visit all nodes in a given graph. A smaller cover time means a higher exploration efficiency of traversal algorithm. Although random walk algorithms have been studied extensively in the existing literature, there has been no cover time result for any non-Markovian method. In this work, we stand on a theoretical perspective and show that the negative feedback strategy (a count-based exploration method) is better than the naive random walk search. In particular, the former strategy can locally improve the search efficiency for an arbitrary graph. It also achieves smaller cover times for special but important graphs, including clique graphs, tree graphs, etc. Moreover, we make connections between our results and reinforcement learning literature to give new insights on why classical UCB and MCTS algorithms are so useful. Various numerical results corroborate our theoretical findings.

Kernel PCA for multivariate extremes

We propose kernel PCA as a method for analyzing the dependence structure of multivariate extremes and demonstrate that it can be a powerful tool for clustering and dimension reduction. Our work provides some theoretical insight into the preimages obtained by kernel PCA, demonstrating that under certain conditions they can effectively identify clusters in the data. We build on these new insights to characterize rigorously the performance of kernel PCA based on an extremal sample, i.e., the angular part of random vectors for which the radius exceeds a large threshold. More specifically, we focus on the asymptotic dependence of multivariate extremes characterized by the angular or spectral measure in extreme value theory and provide a careful analysis in the case where the extremes are generated from a linear factor model. We give theoretical guarantees on the performance of kernel PCA preimages of such extremes by leveraging their asymptotic distribution together with Davis-Kahan perturbation bounds. Our theoretical findings are complemented with numerical experiments illustrating the finite sample performance of our methods.

On Penalization in Stochastic Multi-armed Bandits

We study an important variant of the stochastic multi-armed bandit (MAB) problem, which takes penalization into consideration. Instead of directly maximizing cumulative expected reward, we need to balance between the total reward and fairness level. In this paper, we present some new insights in MAB and formulate the problem in the penalization framework, where rigorous penalized regret can be well defined and more sophisticated regret analysis is possible. Under such a framework, we propose a hard-threshold UCB-like algorithm, which enjoys many merits including asymptotic fairness, nearly optimal regret, better tradeoff between reward and fairness. Both gap-dependent and gap-independent regret bounds have been established. Multiple insightful comments are given to illustrate the soundness of our theoretical analysis. Numerous experimental results corroborate the theory and show the superiority of our method over other existing methods.

Catoni-style Confidence Sequences under Infinite Variance

In this paper, we provide an extension of confidence sequences for settings where the variance of the data-generating distribution does not exist or is infinite. Confidence sequences furnish confidence intervals that are valid at arbitrary data-dependent stopping times, naturally having a wide range of applications. We first establish a lower bound for the width of the Catoni-style confidence sequences for the finite variance case to highlight the looseness of the existing results. Next, we derive tight Catoni-style confidence sequences for data distributions having a relaxed bounded~$p^{th}-$moment, where~$p \in (1,2]$, and strengthen the results for the finite variance case of~$p =2$. The derived results are shown to better than confidence sequences obtained using Dubins-Savage inequality.

Detection of Small Holes by the Scale-Invariant Robust Density-Aware Distance Filtration

A novel topological-data-analytical (TDA) method is proposed to distinguish, from noise, small holes surrounded by high-density regions of a probability density function whose mass is concentrated near a manifold (or more generally, a CW complex) embedded in a high-dimensional Euclidean space. The proposed method is robust against additive noise and outliers. In particular, sample points are allowed to be perturbed away from the manifold. Traditional TDA tools, like those based on the distance filtration, often struggle to distinguish small features from noise, because of their short persistence. An alternative filtration, called Robust Density-Aware Distance (RDAD) filtration, is proposed to prolong the persistence of small holes surrounded by high-density regions. This is achieved by weighting the distance function by the density in the sense of Bell et al. Distance-to-measure is incorporated to enhance stability and mitigate noise due to the density estimation. The utility of the proposed filtration in identifying small holes, as well as its robustness against noise, are illustrated through an analytical example and extensive numerical experiments. Basic mathematical properties of the proposed filtration are proven.

Spectral learning of multivariate extremes

We propose a spectral clustering algorithm for analyzing the dependence structure of multivariate extremes. More specifically, we focus on the asymptotic dependence of multivariate extremes characterized by the angular or spectral measure in extreme value theory. Our work studies the theoretical performance of spectral clustering based on a random $k$-nearest neighbor graph constructed from an extremal sample, i.e., the angular part of random vectors for which the radius exceeds a large threshold. In particular, we derive the asymptotic distribution of extremes arising from a linear factor model and prove that, under certain conditions, spectral clustering can consistently identify the clusters of extremes arising in this model. Leveraging this result we propose a simple consistent estimation strategy for learning the angular measure. Our theoretical findings are complemented with numerical experiments illustrating the finite sample performance of our methods.

Extreme Bandits using Robust Statistics

We consider a multi-armed bandit problem motivated by situations where only the extreme values, as opposed to expected values in the classical bandit setting, are of interest. We propose distribution free algorithms using robust statistics and characterize the statistical properties. We show that the provided algorithms achieve vanishing extremal regret under weaker conditions than existing algorithms. Performance of the algorithms is demonstrated for the finite-sample setting using numerical experiments. The results show superior performance of the proposed algorithms compared to the well known algorithms.