Epsilon*: Privacy Metric for Machine Learning Models

We introduce Epsilon*, a new privacy metric for measuring the privacy risk of a single model instance prior to, during, or after deployment of privacy mitigation strategies. The metric does not require access to the training data sampling or model training algorithm. Epsilon* is a function of true positive and false positive rates in a hypothesis test used by an adversary in a membership inference attack. We distinguish between quantifying the privacy loss of a trained model instance and quantifying the privacy loss of the training mechanism which produces this model instance. Existing approaches in the privacy auditing literature provide lower bounds for the latter, while our metric provides a lower bound for the former by relying on an (${\epsilon}$,${\delta}$)-type of quantification of the privacy of the trained model instance. We establish a relationship between these lower bounds and show how to implement Epsilon* to avoid numerical and noise amplification instability. We further show in experiments on benchmark public data sets that Epsilon* is sensitive to privacy risk mitigation by training with differential privacy (DP), where the value of Epsilon* is reduced by up to 800% compared to the Epsilon* values of non-DP trained baseline models. This metric allows privacy auditors to be independent of model owners, and enables all decision-makers to visualize the privacy-utility landscape to make informed decisions regarding the trade-offs between model privacy and utility.

Sales Channel Optimization via Simulations Based on Observational Data with Delayed Rewards: A Case Study at LinkedIn

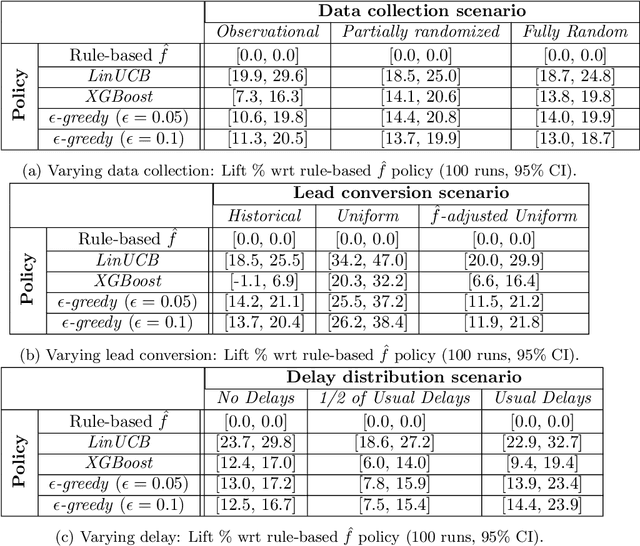
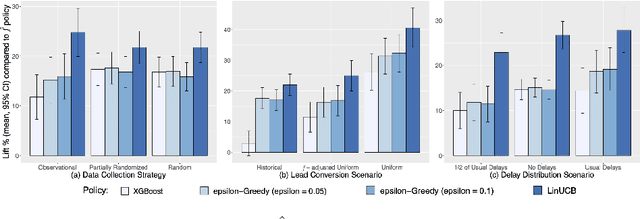
Training models on data obtained from randomized experiments is ideal for making good decisions. However, randomized experiments are often time-consuming, expensive, risky, infeasible or unethical to perform, leaving decision makers little choice but to rely on observational data collected under historical policies when training models. This opens questions regarding not only which decision-making policies would perform best in practice, but also regarding the impact of different data collection protocols on the performance of various policies trained on the data, or the robustness of policy performance with respect to changes in problem characteristics such as action- or reward- specific delays in observing outcomes. We aim to answer such questions for the problem of optimizing sales channel allocations at LinkedIn, where sales accounts (leads) need to be allocated to one of three channels, with the goal of maximizing the number of successful conversions over a period of time. A key problem feature constitutes the presence of stochastic delays in observing allocation outcomes, whose distribution is both channel- and outcome- dependent. We built a discrete-time simulation that can handle our problem features and used it to evaluate: a) a historical rule-based policy; b) a supervised machine learning policy (XGBoost); and c) multi-armed bandit (MAB) policies, under different scenarios involving: i) data collection used for training (observational vs randomized); ii) lead conversion scenarios; iii) delay distributions. Our simulation results indicate that LinUCB, a simple MAB policy, consistently outperforms the other policies, achieving a 18-47% lift relative to a rule-based policy