Differential Privacy Under Class Imbalance: Methods and Empirical Insights

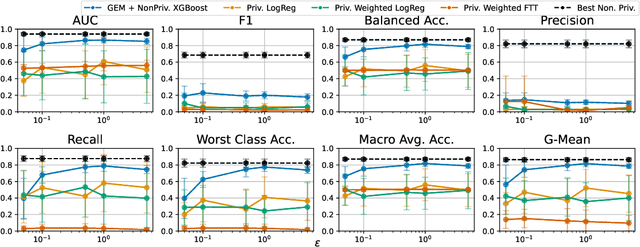
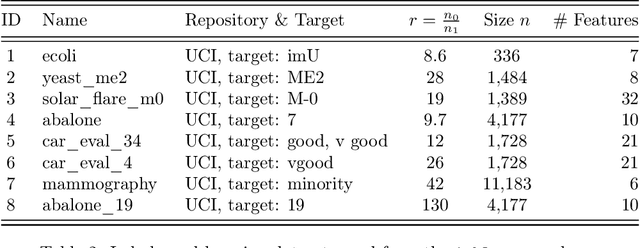
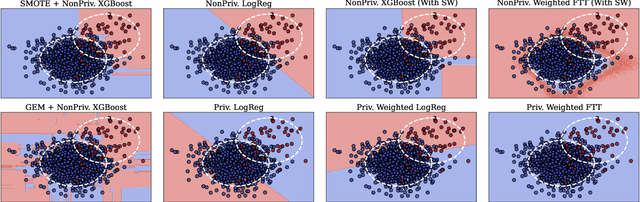
Imbalanced learning occurs in classification settings where the distribution of class-labels is highly skewed in the training data, such as when predicting rare diseases or in fraud detection. This class imbalance presents a significant algorithmic challenge, which can be further exacerbated when privacy-preserving techniques such as differential privacy are applied to protect sensitive training data. Our work formalizes these challenges and provides a number of algorithmic solutions. We consider DP variants of pre-processing methods that privately augment the original dataset to reduce the class imbalance; these include oversampling, SMOTE, and private synthetic data generation. We also consider DP variants of in-processing techniques, which adjust the learning algorithm to account for the imbalance; these include model bagging, class-weighted empirical risk minimization and class-weighted deep learning. For each method, we either adapt an existing imbalanced learning technique to the private setting or demonstrate its incompatibility with differential privacy. Finally, we empirically evaluate these privacy-preserving imbalanced learning methods under various data and distributional settings. We find that private synthetic data methods perform well as a data pre-processing step, while class-weighted ERMs are an alternative in higher-dimensional settings where private synthetic data suffers from the curse of dimensionality.

Epsilon*: Privacy Metric for Machine Learning Models

We introduce Epsilon*, a new privacy metric for measuring the privacy risk of a single model instance prior to, during, or after deployment of privacy mitigation strategies. The metric does not require access to the training data sampling or model training algorithm. Epsilon* is a function of true positive and false positive rates in a hypothesis test used by an adversary in a membership inference attack. We distinguish between quantifying the privacy loss of a trained model instance and quantifying the privacy loss of the training mechanism which produces this model instance. Existing approaches in the privacy auditing literature provide lower bounds for the latter, while our metric provides a lower bound for the former by relying on an (${\epsilon}$,${\delta}$)-type of quantification of the privacy of the trained model instance. We establish a relationship between these lower bounds and show how to implement Epsilon* to avoid numerical and noise amplification instability. We further show in experiments on benchmark public data sets that Epsilon* is sensitive to privacy risk mitigation by training with differential privacy (DP), where the value of Epsilon* is reduced by up to 800% compared to the Epsilon* values of non-DP trained baseline models. This metric allows privacy auditors to be independent of model owners, and enables all decision-makers to visualize the privacy-utility landscape to make informed decisions regarding the trade-offs between model privacy and utility.

Privately detecting changes in unknown distributions

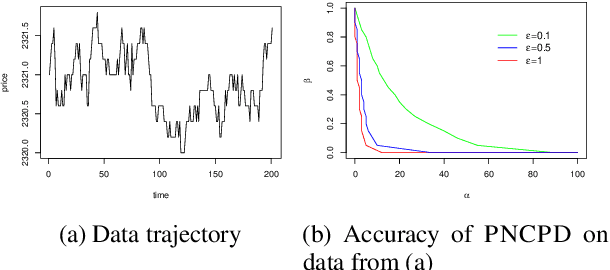
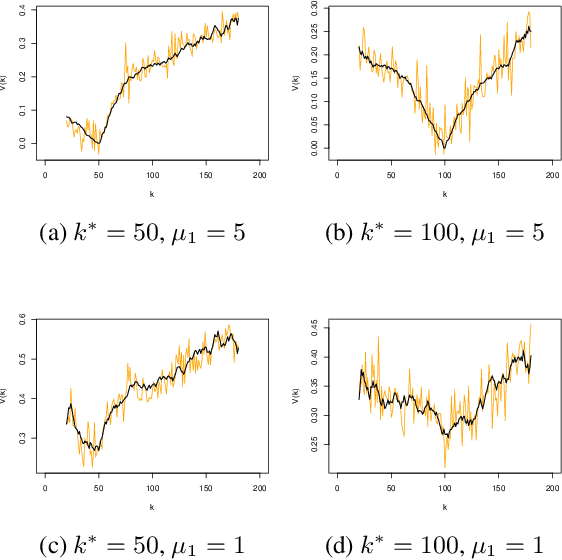
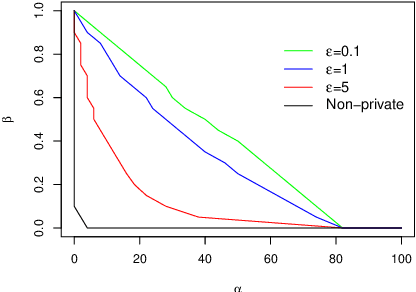
The change-point detection problem seeks to identify distributional changes in streams of data. Increasingly, tools for change-point detection are applied in settings where data may be highly sensitive and formal privacy guarantees are required, such as identifying disease outbreaks based on hospital records, or IoT devices detecting activity within a home. Differential privacy has emerged as a powerful technique for enabling data analysis while preventing information leakage about individuals. Much of the prior work on change-point detection (including the only private algorithms for this problem) requires complete knowledge of the pre-change and post-change distributions. However, this assumption is not realistic for many practical applications of interest. This work develops differentially private algorithms for solving the change-point problem when the data distributions are unknown. Additionally, the data may be sampled from distributions that change smoothly over time, rather than fixed pre-change and post-change distributions. We apply our algorithms to detect changes in the linear trends of such data streams.