Scalable Differentially Private Bayesian Optimization

In recent years, there has been much work on scaling Bayesian Optimization to high-dimensional problems, for example hyperparameter tuning in large neural network models. These scalable methods have been successful, finding high objective values much more quickly than traditional global Bayesian Optimization or random search-based methods. At the same time, these large neural network models often use sensitive data, but preservation of Differential Privacy has not scaled alongside these modern Bayesian Optimization procedures. Here we develop a method to privately estimate potentially high-dimensional parameter spaces using Gradient Informative Bayesian Optimization. Our theoretical results prove that under suitable conditions, our method converges exponentially fast to a ball around the optimal parameter configuration. Moreover, regardless of whether the assumptions are satisfied, we show that our algorithm maintains privacy and empirically demonstrates superior performance to existing methods in the high-dimensional hyperparameter setting.

Differential Privacy Under Class Imbalance: Methods and Empirical Insights

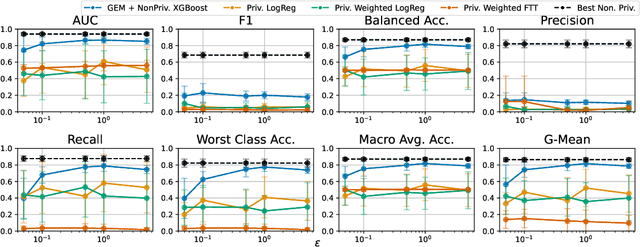
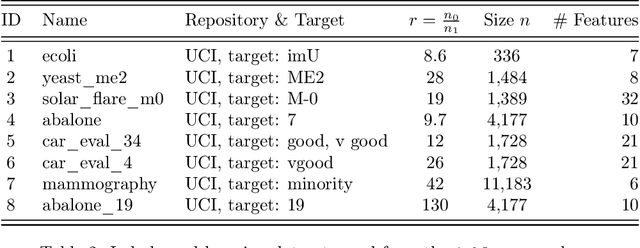
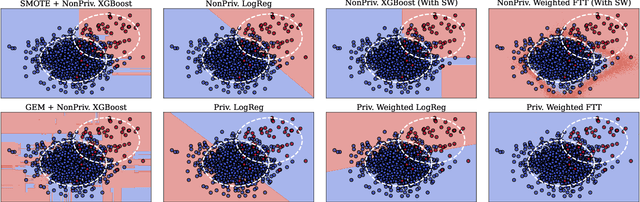
Imbalanced learning occurs in classification settings where the distribution of class-labels is highly skewed in the training data, such as when predicting rare diseases or in fraud detection. This class imbalance presents a significant algorithmic challenge, which can be further exacerbated when privacy-preserving techniques such as differential privacy are applied to protect sensitive training data. Our work formalizes these challenges and provides a number of algorithmic solutions. We consider DP variants of pre-processing methods that privately augment the original dataset to reduce the class imbalance; these include oversampling, SMOTE, and private synthetic data generation. We also consider DP variants of in-processing techniques, which adjust the learning algorithm to account for the imbalance; these include model bagging, class-weighted empirical risk minimization and class-weighted deep learning. For each method, we either adapt an existing imbalanced learning technique to the private setting or demonstrate its incompatibility with differential privacy. Finally, we empirically evaluate these privacy-preserving imbalanced learning methods under various data and distributional settings. We find that private synthetic data methods perform well as a data pre-processing step, while class-weighted ERMs are an alternative in higher-dimensional settings where private synthetic data suffers from the curse of dimensionality.

Kernel PCA for multivariate extremes

We propose kernel PCA as a method for analyzing the dependence structure of multivariate extremes and demonstrate that it can be a powerful tool for clustering and dimension reduction. Our work provides some theoretical insight into the preimages obtained by kernel PCA, demonstrating that under certain conditions they can effectively identify clusters in the data. We build on these new insights to characterize rigorously the performance of kernel PCA based on an extremal sample, i.e., the angular part of random vectors for which the radius exceeds a large threshold. More specifically, we focus on the asymptotic dependence of multivariate extremes characterized by the angular or spectral measure in extreme value theory and provide a careful analysis in the case where the extremes are generated from a linear factor model. We give theoretical guarantees on the performance of kernel PCA preimages of such extremes by leveraging their asymptotic distribution together with Davis-Kahan perturbation bounds. Our theoretical findings are complemented with numerical experiments illustrating the finite sample performance of our methods.

Differentially private inference via noisy optimization

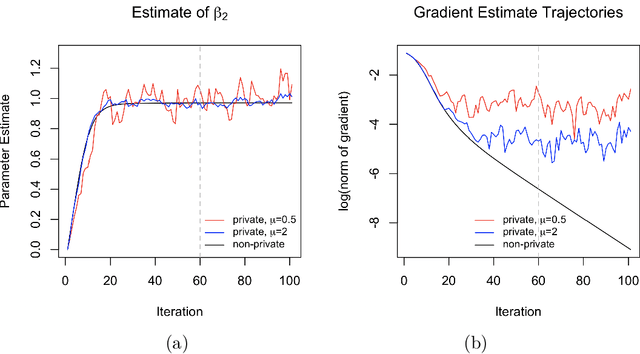
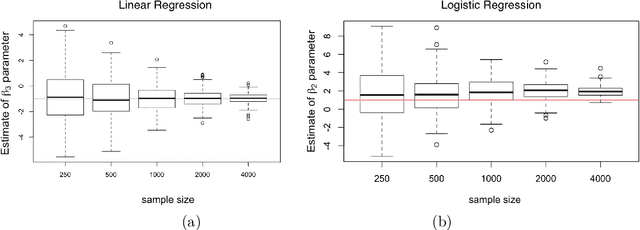
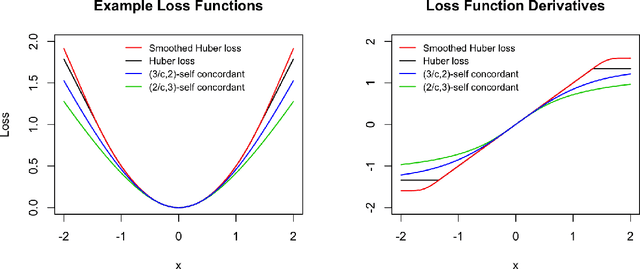
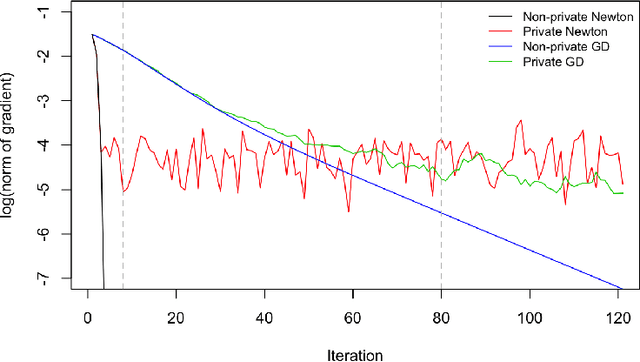
We propose a general optimization-based framework for computing differentially private M-estimators and a new method for constructing differentially private confidence regions. Firstly, we show that robust statistics can be used in conjunction with noisy gradient descent or noisy Newton methods in order to obtain optimal private estimators with global linear or quadratic convergence, respectively. We establish local and global convergence guarantees, under both local strong convexity and self-concordance, showing that our private estimators converge with high probability to a nearly optimal neighborhood of the non-private M-estimators. Secondly, we tackle the problem of parametric inference by constructing differentially private estimators of the asymptotic variance of our private M-estimators. This naturally leads to approximate pivotal statistics for constructing confidence regions and conducting hypothesis testing. We demonstrate the effectiveness of a bias correction that leads to enhanced small-sample empirical performance in simulations. We illustrate the benefits of our methods in several numerical examples.

Propose, Test, Release: Differentially private estimation with high probability

We derive concentration inequalities for differentially private median and mean estimators building on the "Propose, Test, Release" (PTR) mechanism introduced by Dwork and Lei (2009). We introduce a new general version of the PTR mechanism that allows us to derive high probability error bounds for differentially private estimators. Our algorithms provide the first statistical guarantees for differentially private estimation of the median and mean without any boundedness assumptions on the data, and without assuming that the target population parameter lies in some known bounded interval. Our procedures do not rely on any truncation of the data and provide the first sub-Gaussian high probability bounds for differentially private median and mean estimation, for possibly heavy tailed random variables.

Privacy-preserving parametric inference: a case for robust statistics

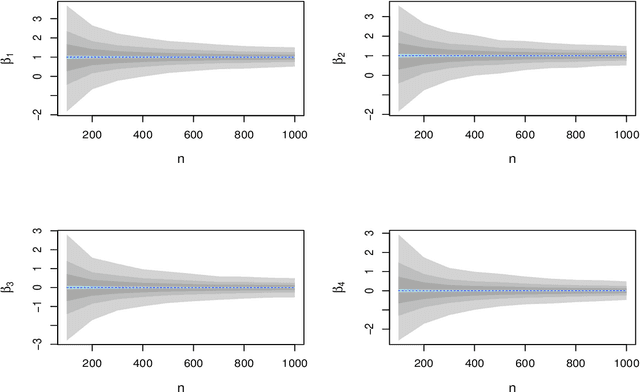
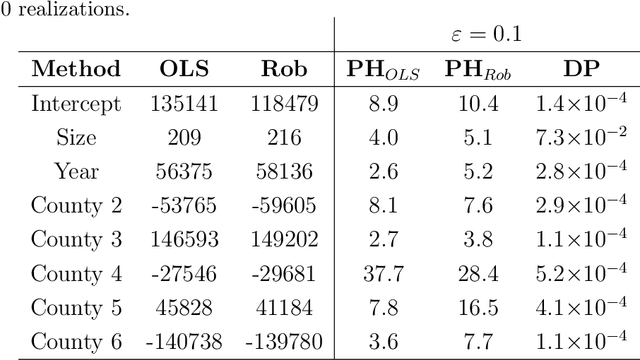
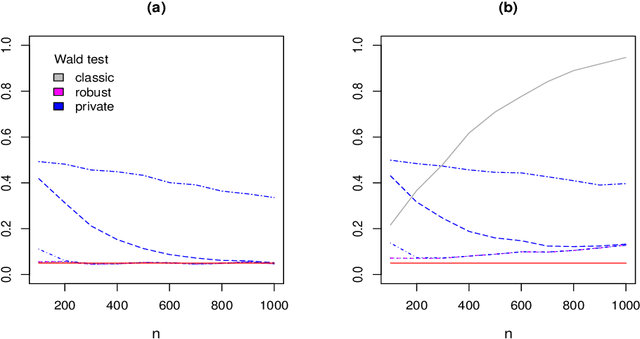
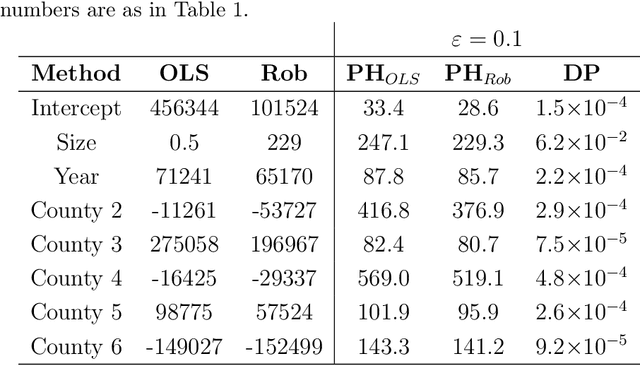
Differential privacy is a cryptographically-motivated approach to privacy that has become a very active field of research over the last decade in theoretical computer science and machine learning. In this paradigm one assumes there is a trusted curator who holds the data of individuals in a database and the goal of privacy is to simultaneously protect individual data while allowing the release of global characteristics of the database. In this setting we introduce a general framework for parametric inference with differential privacy guarantees. We first obtain differentially private estimators based on bounded influence M-estimators by leveraging their gross-error sensitivity in the calibration of a noise term added to them in order to ensure privacy. We then show how a similar construction can also be applied to construct differentially private test statistics analogous to the Wald, score and likelihood ratio tests. We provide statistical guarantees for all our proposals via an asymptotic analysis. An interesting consequence of our results is to further clarify the connection between differential privacy and robust statistics. In particular, we demonstrate that differential privacy is a weaker stability requirement than infinitesimal robustness, and show that robust M-estimators can be easily randomized in order to guarantee both differential privacy and robustness towards the presence of contaminated data. We illustrate our results both on simulated and real data.

Differentially private sub-Gaussian location estimators

We tackle the problem of estimating a location parameter with differential privacy guarantees and sub-Gaussian deviations. Recent work in statistics has focused on the study of estimators that achieve sub-Gaussian type deviations even for heavy tailed data. We revisit some of these estimators through the lens of differential privacy and show that a naive application of the Laplace mechanism can lead to sub-optimal results. We design two private algorithms for estimating the median that lead to estimators with sub-Gaussian type errors. Unlike most existing differentially private median estimators, both algorithms are well defined for unbounded random variables that are not even required to have finite moments. We then turn to the problem of sub-Gaussian mean estimation and show that under heavy tails natural differentially private alternatives lead to strictly worse deviations than their non-private sub-Gaussian counterparts. This is in sharp contrast with recent results that show that from an asymptotic perspective the cost of differential privacy is negligible.

Centrality measures for graphons: Accounting for uncertainty in networks

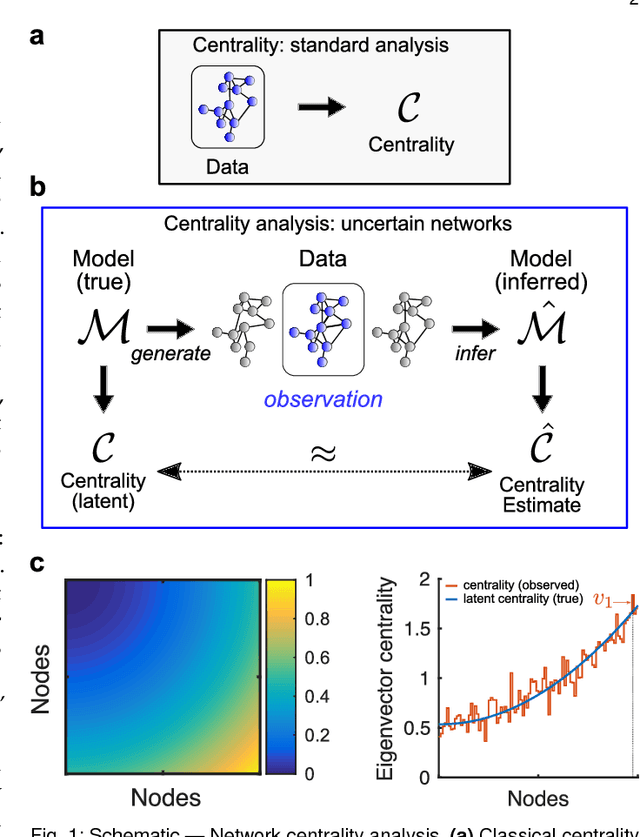
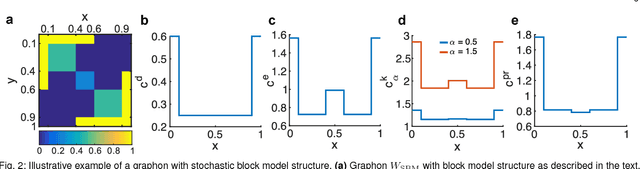
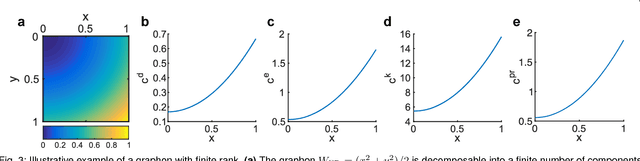
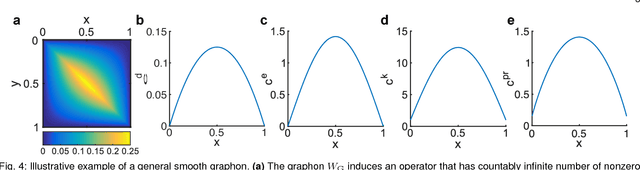
As relational datasets modeled as graphs keep increasing in size and their data-acquisition is permeated by uncertainty, graph-based analysis techniques can become computationally and conceptually challenging. In particular, node centrality measures rely on the assumption that the graph is perfectly known -- a premise not necessarily fulfilled for large, uncertain networks. Accordingly, centrality measures may fail to faithfully extract the importance of nodes in the presence of uncertainty. To mitigate these problems, we suggest a statistical approach based on graphon theory: we introduce formal definitions of centrality measures for graphons and establish their connections to classical graph centrality measures. A key advantage of this approach is that centrality measures defined at the modeling level of graphons are inherently robust to stochastic variations of specific graph realizations. Using the theory of linear integral operators, we define degree, eigenvector, Katz and PageRank centrality functions for graphons and establish concentration inequalities demonstrating that graphon centrality functions arise naturally as limits of their counterparts defined on sequences of graphs of increasing size. The same concentration inequalities also provide high-probability bounds between the graphon centrality functions and the centrality measures on any sampled graph, thereby establishing a measure of uncertainty of the measured centrality score.