Model-Driven Graph Contrastive Learning

We propose $\textbf{MGCL}$, a model-driven graph contrastive learning (GCL) framework that leverages graphons (probabilistic generative models for graphs) to guide contrastive learning by accounting for the data's underlying generative process. GCL has emerged as a powerful self-supervised framework for learning expressive node or graph representations without relying on annotated labels, which are often scarce in real-world data. By contrasting augmented views of graph data, GCL has demonstrated strong performance across various downstream tasks, such as node and graph classification. However, existing methods typically rely on manually designed or heuristic augmentation strategies that are not tailored to the underlying data distribution and operate at the individual graph level, ignoring similarities among graphs generated from the same model. Conversely, in our proposed approach, MGCL first estimates the graphon associated with the observed data and then defines a graphon-informed augmentation process, enabling data-adaptive and principled augmentations. Additionally, for graph-level tasks, MGCL clusters the dataset and estimates a graphon per group, enabling contrastive pairs to reflect shared semantics and structure. Extensive experiments on benchmark datasets demonstrate that MGCL achieves state-of-the-art performance, highlighting the advantages of incorporating generative models into GCL.

Infinity Search: Approximate Vector Search with Projections on q-Metric Spaces

Despite the ubiquity of vector search applications, prevailing search algorithms overlook the metric structure of vector embeddings, treating it as a constraint rather than exploiting its underlying properties. In this paper, we demonstrate that in $q$-metric spaces, metric trees can leverage a stronger version of the triangle inequality to reduce comparisons for exact search. Notably, as $q$ approaches infinity, the search complexity becomes logarithmic. Therefore, we propose a novel projection method that embeds vector datasets with arbitrary dissimilarity measures into $q$-metric spaces while preserving the nearest neighbor. We propose to learn an approximation of this projection to efficiently transform query points to a space where euclidean distances satisfy the desired properties. Our experimental results with text and image vector embeddings show that learning $q$-metric approximations enables classic metric tree algorithms -- which typically underperform with high-dimensional data -- to achieve competitive performance against state-of-the-art search methods.

A Few Moments Please: Scalable Graphon Learning via Moment Matching

Graphons, as limit objects of dense graph sequences, play a central role in the statistical analysis of network data. However, existing graphon estimation methods often struggle with scalability to large networks and resolution-independent approximation, due to their reliance on estimating latent variables or costly metrics such as the Gromov-Wasserstein distance. In this work, we propose a novel, scalable graphon estimator that directly recovers the graphon via moment matching, leveraging implicit neural representations (INRs). Our approach avoids latent variable modeling by training an INR--mapping coordinates to graphon values--to match empirical subgraph counts (i.e., moments) from observed graphs. This direct estimation mechanism yields a polynomial-time solution and crucially sidesteps the combinatorial complexity of Gromov-Wasserstein optimization. Building on foundational results, we establish a theoretical guarantee: when the observed subgraph motifs sufficiently represent those of the true graphon (a condition met with sufficiently large or numerous graph samples), the estimated graphon achieves a provable upper bound in cut distance from the ground truth. Additionally, we introduce MomentMixup, a data augmentation technique that performs mixup in the moment space to enhance graphon-based learning. Our graphon estimation method achieves strong empirical performance--demonstrating high accuracy on small graphs and superior computational efficiency on large graphs--outperforming state-of-the-art scalable estimators in 75\% of benchmark settings and matching them in the remaining cases. Furthermore, MomentMixup demonstrated improved graph classification accuracy on the majority of our benchmarks.

Graph Guided Diffusion: Unified Guidance for Conditional Graph Generation

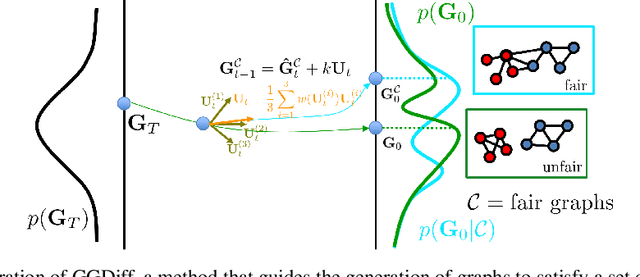
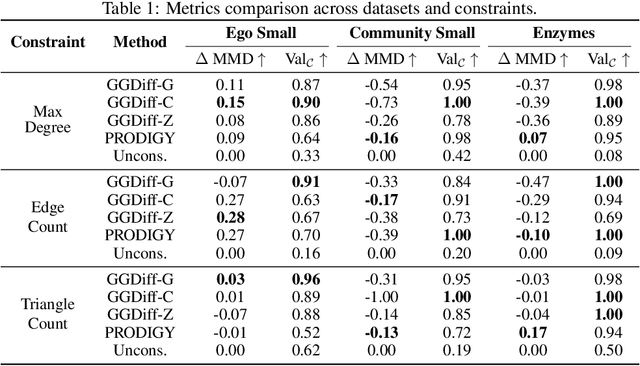
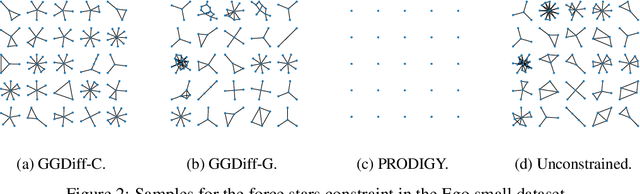
Diffusion models have emerged as powerful generative models for graph generation, yet their use for conditional graph generation remains a fundamental challenge. In particular, guiding diffusion models on graphs under arbitrary reward signals is difficult: gradient-based methods, while powerful, are often unsuitable due to the discrete and combinatorial nature of graphs, and non-differentiable rewards further complicate gradient-based guidance. We propose Graph Guided Diffusion (GGDiff), a novel guidance framework that interprets conditional diffusion on graphs as a stochastic control problem to address this challenge. GGDiff unifies multiple guidance strategies, including gradient-based guidance (for differentiable rewards), control-based guidance (using control signals from forward reward evaluations), and zero-order approximations (bridging gradient-based and gradient-free optimization). This comprehensive, plug-and-play framework enables zero-shot guidance of pre-trained diffusion models under both differentiable and non-differentiable reward functions, adapting well-established guidance techniques to graph generation--a direction largely unexplored. Our formulation balances computational efficiency, reward alignment, and sample quality, enabling practical conditional generation across diverse reward types. We demonstrate the efficacy of GGDiff in various tasks, including constraints on graph motifs, fairness, and link prediction, achieving superior alignment with target rewards while maintaining diversity and fidelity.

SeLR: Sparsity-enhanced Lagrangian Relaxation for Computation Offloading at the Edge

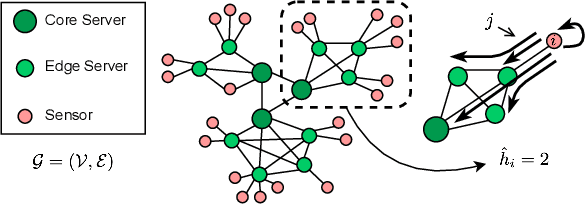
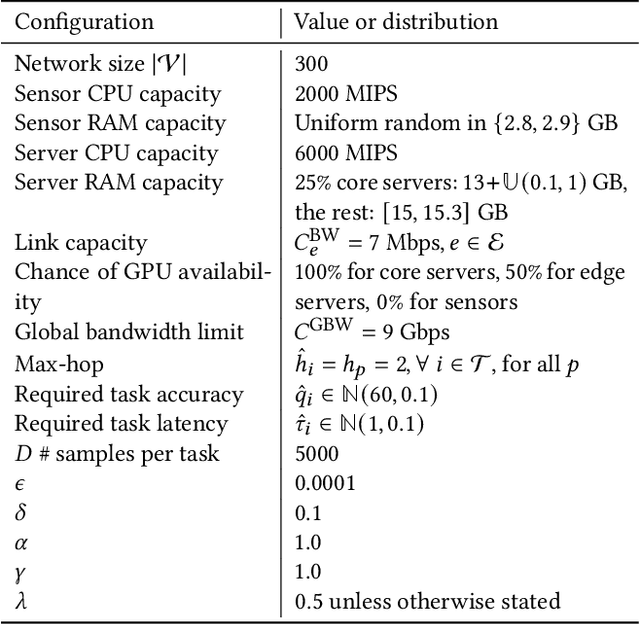
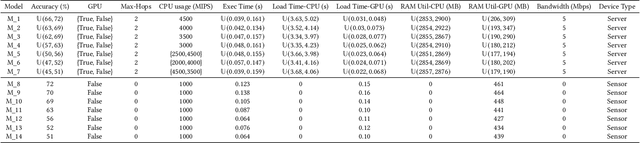
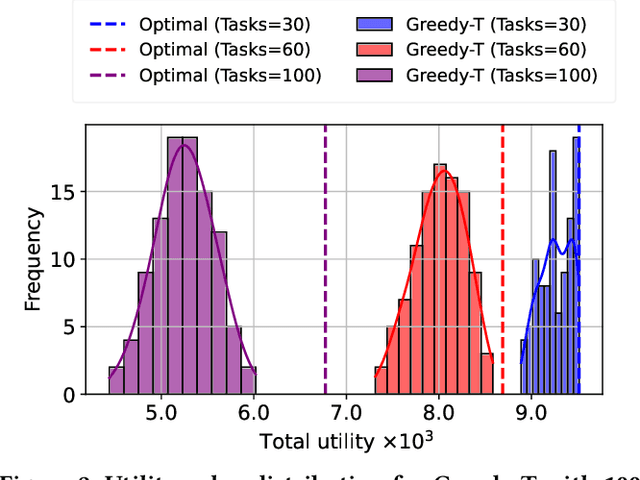
This paper introduces a novel computational approach for offloading sensor data processing tasks to servers in edge networks for better accuracy and makespan. A task is assigned with one of several offloading options, each comprises a server, a route for uploading data to the server, and a service profile that specifies the performance and resource consumption at the server and in the network. This offline offloading and routing problem is formulated as mixed integer programming (MIP), which is non-convex and HP-hard due to the discrete decision variables associated to the offloading options. The novelty of our approach is to transform this non-convex problem into iterative convex optimization by relaxing integer decision variables into continuous space, combining primal-dual optimization for penalizing constraint violations and reweighted $L_1$-minimization for promoting solution sparsity, which achieves better convergence through a smoother path in a continuous search space. Compared to existing greedy heuristics, our approach can achieve a better Pareto frontier in accuracy and latency, scales better to larger problem instances, and can achieve a 7.72--9.17$\times$ reduction in computational overhead of scheduling compared to the optimal solver in hierarchically organized edge networks with 300 nodes and 50--100 tasks.

Generalizing Biased Backpressure Routing and Scheduling to Wireless Multi-hop Networks with Advanced Air-interfaces

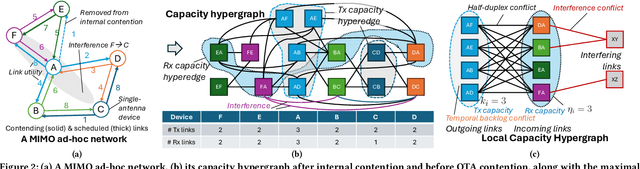
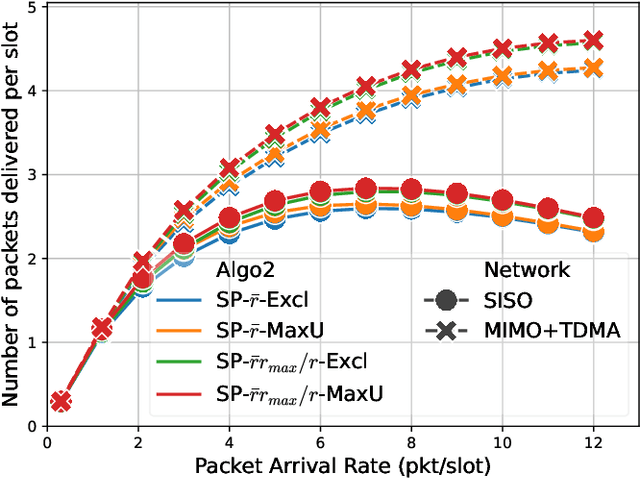
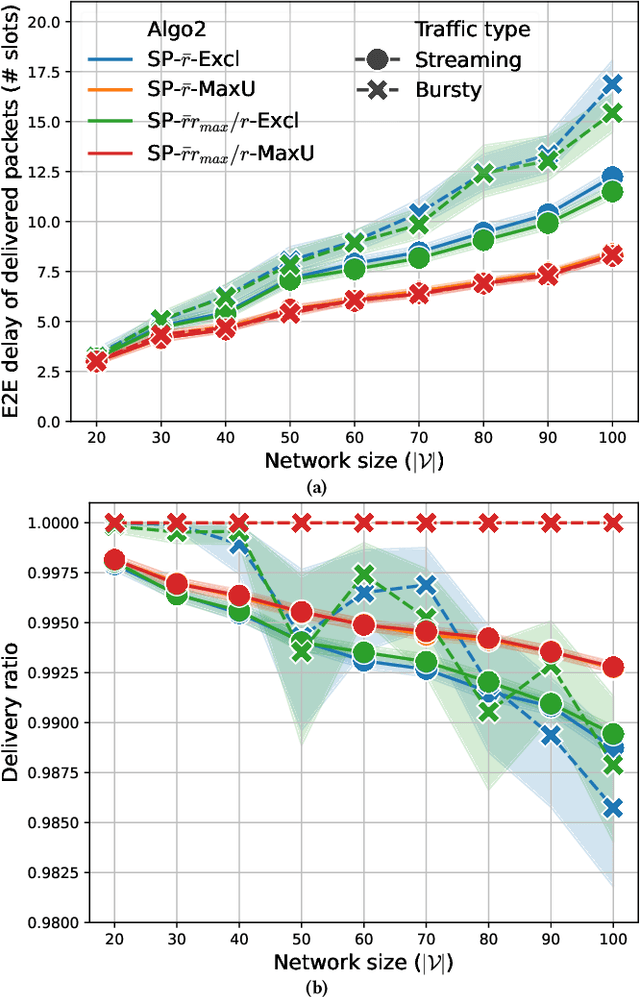
Backpressure (BP) routing and scheduling is a well-established resource allocation method for wireless multi-hop networks, known for its fully distributed operations and proven maximum queue stability. Recent advances in shortest path-biased BP routing (SP-BP) mitigate shortcomings such as slow startup and random walk, but exclusive link-level commodity selection still suffers from the last-packet problem and bandwidth underutilization. Moreover, classic BP routing implicitly assumes single-input-single-output (SISO) transceivers, which can lead to the same packets being scheduled on multiple outgoing links for multiple-input-multiple-output (MIMO) transceivers, causing detouring and looping in MIMO networks. In this paper, we revisit the foundational Lyapunov drift theory underlying BP routing and demonstrate that exclusive commodity selection is unnecessary, and instead propose a Max-Utility link-sharing method. Additionally, we generalize MaxWeight scheduling to MIMO networks by introducing attributed capacity hypergraphs (ACH), an extension of traditional conflict graphs for SISO networks, and by incorporating backlog reassignment into scheduling iterations to prevent redundant packet routing. Numerical evaluations show that our approach substantially mitigates the last-packet problem in state-of-the-art (SOTA) SP-BP under lightweight traffic, and slightly expands the network capacity region for heavier traffic.

Joint Task Offloading and Routing in Wireless Multi-hop Networks Using Biased Backpressure Algorithm

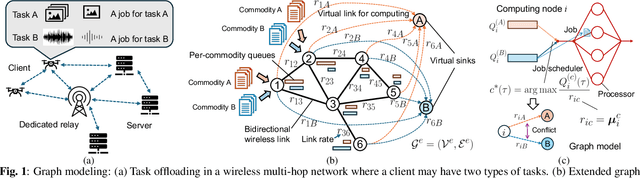
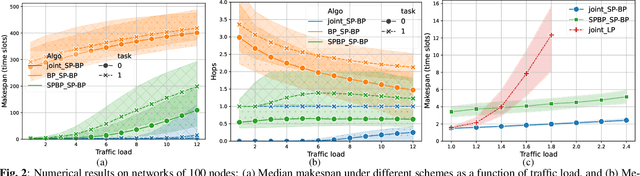
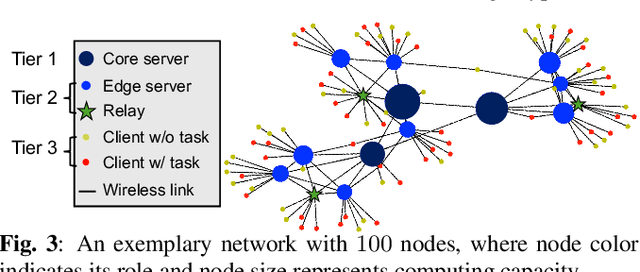
A significant challenge for computation offloading in wireless multi-hop networks is the complex interaction among traffic flows in the presence of interference. Existing approaches often ignore these key effects and/or rely on outdated queueing and channel state information. To fill these gaps, we reformulate joint offloading and routing as a routing problem on an extended graph with physical and virtual links. We adopt the state-of-the-art shortest path-biased Backpressure routing algorithm, which allows the destination and the route of a job to be dynamically adjusted at every time step based on network-wide long-term information and real-time states of local neighborhoods. In large networks, our approach achieves smaller makespan than existing approaches, such as separated Backpressure offloading and joint offloading and routing based on linear programming.

Fully Distributed Online Training of Graph Neural Networks in Networked Systems

Graph neural networks (GNNs) are powerful tools for developing scalable, decentralized artificial intelligence in large-scale networked systems, such as wireless networks, power grids, and transportation networks. Currently, GNNs in networked systems mostly follow a paradigm of `centralized training, distributed execution', which limits their adaptability and slows down their development cycles. In this work, we fill this gap for the first time by developing a communication-efficient, fully distributed online training approach for GNNs applied to large networked systems. For a mini-batch with $B$ samples, our approach of training an $L$-layer GNN only adds $L$ rounds of message passing to the $LB$ rounds required by GNN inference, with doubled message sizes. Through numerical experiments in graph-based node regression, power allocation, and link scheduling in wireless networks, we demonstrate the effectiveness of our approach in training GNNs under supervised, unsupervised, and reinforcement learning paradigms.

Structure-Guided Input Graph for GNNs facing Heterophily

Graph Neural Networks (GNNs) have emerged as a promising tool to handle data exhibiting an irregular structure. However, most GNN architectures perform well on homophilic datasets, where the labels of neighboring nodes are likely to be the same. In recent years, an increasing body of work has been devoted to the development of GNN architectures for heterophilic datasets, where labels do not exhibit this low-pass behavior. In this work, we create a new graph in which nodes are connected if they share structural characteristics, meaning a higher chance of sharing their labels, and then use this new graph in the GNN architecture. To do this, we compute the k-nearest neighbors graph according to distances between structural features, which are either (i) role-based, such as degree, or (ii) global, such as centrality measures. Experiments show that the labels are smoother in this newly defined graph and that the performance of GNN architectures improves when using this alternative structure.

Learning state and proposal dynamics in state-space models using differentiable particle filters and neural networks

State-space models are a popular statistical framework for analysing sequential data. Within this framework, particle filters are often used to perform inference on non-linear state-space models. We introduce a new method, StateMixNN, that uses a pair of neural networks to learn the proposal distribution and transition distribution of a particle filter. Both distributions are approximated using multivariate Gaussian mixtures. The component means and covariances of these mixtures are learnt as outputs of learned functions. Our method is trained targeting the log-likelihood, thereby requiring only the observation series, and combines the interpretability of state-space models with the flexibility and approximation power of artificial neural networks. The proposed method significantly improves recovery of the hidden state in comparison with the state-of-the-art, showing greater improvement in highly non-linear scenarios.