Precision Neural Networks: Joint Graph And Relational Learning

CoVariance Neural Networks (VNNs) perform convolutions on the graph determined by the covariance matrix of the data, which enables expressive and stable covariance-based learning. However, covariance matrices are typically dense, fail to encode conditional independence, and are often precomputed in a task-agnostic way, which may hinder performance. To overcome these limitations, we study Precision Neural Networks (PNNs), i.e., VNNs on the precision matrix -- the inverse covariance. The precision matrix naturally encodes statistical independence, often exhibits sparsity, and preserves the covariance spectral structure. To make precision estimation task-aware, we formulate an optimization problem that jointly learns the network parameters and the precision matrix, and solve it via alternating optimization, by sequentially updating the network weights and the precision estimate. We theoretically bound the distance between the estimated and true precision matrices at each iteration, and demonstrate the effectiveness of joint estimation compared to two-step approaches on synthetic and real-world data.

Directed Acyclic Graph Convolutional Networks

Directed acyclic graphs (DAGs) are central to science and engineering applications including causal inference, scheduling, and neural architecture search. In this work, we introduce the DAG Convolutional Network (DCN), a novel graph neural network (GNN) architecture designed specifically for convolutional learning from signals supported on DAGs. The DCN leverages causal graph filters to learn nodal representations that account for the partial ordering inherent to DAGs, a strong inductive bias does not present in conventional GNNs. Unlike prior art in machine learning over DAGs, DCN builds on formal convolutional operations that admit spectral-domain representations. We further propose the Parallel DCN (PDCN), a model that feeds input DAG signals to a parallel bank of causal graph-shift operators and processes these DAG-aware features using a shared multilayer perceptron. This way, PDCN decouples model complexity from graph size while maintaining satisfactory predictive performance. The architectures' permutation equivariance and expressive power properties are also established. Comprehensive numerical tests across several tasks, datasets, and experimental conditions demonstrate that (P)DCN compares favorably with state-of-the-art baselines in terms of accuracy, robustness, and computational efficiency. These results position (P)DCN as a viable framework for deep learning from DAG-structured data that is designed from first (graph) signal processing principles.

Adapting to Heterophilic Graph Data with Structure-Guided Neighbor Discovery

Graph Neural Networks (GNNs) often struggle with heterophilic data, where connected nodes may have dissimilar labels, as they typically assume homophily and rely on local message passing. To address this, we propose creating alternative graph structures by linking nodes with similar structural attributes (e.g., role-based or global), thereby fostering higher label homophily on these new graphs. We theoretically prove that GNN performance can be improved by utilizing graphs with fewer false positive edges (connections between nodes of different classes) and that considering multiple graph views increases the likelihood of finding such beneficial structures. Building on these insights, we introduce Structure-Guided GNN (SG-GNN), an architecture that processes the original graph alongside the newly created structural graphs, adaptively learning to weigh their contributions. Extensive experiments on various benchmark datasets, particularly those with heterophilic characteristics, demonstrate that our SG-GNN achieves state-of-the-art or highly competitive performance, highlighting the efficacy of exploiting structural information to guide GNNs.

Enhancing Graphical Lasso: A Robust Scheme for Non-Stationary Mean Data

This work addresses the problem of graph learning from data following a Gaussian Graphical Model (GGM) with a time-varying mean. Graphical Lasso (GL), the standard method for estimating sparse precision matrices, assumes that the observed data follows a zero-mean Gaussian distribution. However, this assumption is often violated in real-world scenarios where the mean evolves over time due to external influences, trends, or regime shifts. When the mean is not properly accounted for, applying GL directly can lead to estimating a biased precision matrix, hence hindering the graph learning task. To overcome this limitation, we propose Graphical Lasso with Adaptive Targeted Adaptive Importance Sampling (GL-ATAIS), an iterative method that jointly estimates the time-varying mean and the precision matrix. Our approach integrates Bayesian inference with frequentist estimation, leveraging importance sampling to obtain an estimate of the mean while using a regularized maximum likelihood estimator to infer the precision matrix. By iteratively refining both estimates, GL-ATAIS mitigates the bias introduced by time-varying means, leading to more accurate graph recovery. Our numerical evaluation demonstrates the impact of properly accounting for time-dependent means and highlights the advantages of GL-ATAIS over standard GL in recovering the true graph structure.

Structure-Guided Input Graph for GNNs facing Heterophily

Graph Neural Networks (GNNs) have emerged as a promising tool to handle data exhibiting an irregular structure. However, most GNN architectures perform well on homophilic datasets, where the labels of neighboring nodes are likely to be the same. In recent years, an increasing body of work has been devoted to the development of GNN architectures for heterophilic datasets, where labels do not exhibit this low-pass behavior. In this work, we create a new graph in which nodes are connected if they share structural characteristics, meaning a higher chance of sharing their labels, and then use this new graph in the GNN architecture. To do this, we compute the k-nearest neighbors graph according to distances between structural features, which are either (i) role-based, such as degree, or (ii) global, such as centrality measures. Experiments show that the labels are smoother in this newly defined graph and that the performance of GNN architectures improves when using this alternative structure.

Online Learning Of Expanding Graphs

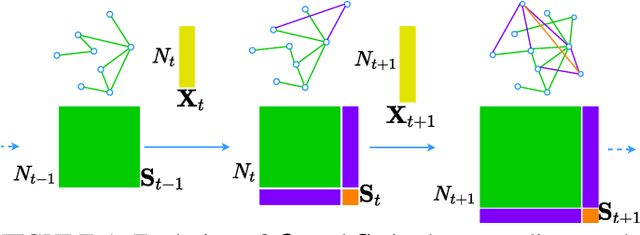
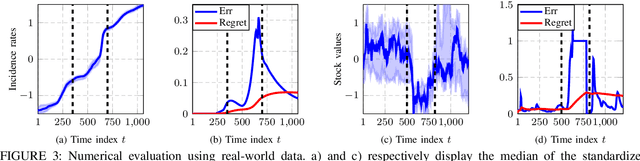
This paper addresses the problem of online network topology inference for expanding graphs from a stream of spatiotemporal signals. Online algorithms for dynamic graph learning are crucial in delay-sensitive applications or when changes in topology occur rapidly. While existing works focus on inferring the connectivity within a fixed set of nodes, in practice, the graph can grow as new nodes join the network. This poses additional challenges like modeling temporal dynamics involving signals and graphs of different sizes. This growth also increases the computational complexity of the learning process, which may become prohibitive. To the best of our knowledge, this is the first work to tackle this setting. We propose a general online algorithm based on projected proximal gradient descent that accounts for the increasing graph size at each iteration. Recursively updating the sample covariance matrix is a key aspect of our approach. We introduce a strategy that enables different types of updates for nodes that just joined the network and for previously existing nodes. To provide further insights into the proposed method, we specialize it in Gaussian Markov random field settings, where we analyze the computational complexity and characterize the dynamic cumulative regret. Finally, we demonstrate the effectiveness of the proposed approach using both controlled experiments and real-world datasets from epidemic and financial networks.

Redesigning graph filter-based GNNs to relax the homophily assumption

Graph neural networks (GNNs) have become a workhorse approach for learning from data defined over irregular domains, typically by implicitly assuming that the data structure is represented by a homophilic graph. However, recent works have revealed that many relevant applications involve heterophilic data where the performance of GNNs can be notably compromised. To address this challenge, we present a simple yet effective architecture designed to mitigate the limitations of the homophily assumption. The proposed architecture reinterprets the role of graph filters in convolutional GNNs, resulting in a more general architecture while incorporating a stronger inductive bias than GNNs based on filter banks. The proposed convolutional layer enhances the expressive capacity of the architecture enabling it to learn from both homophilic and heterophilic data and preventing the issue of oversmoothing. From a theoretical standpoint, we show that the proposed architecture is permutation equivariant. Finally, we show that the proposed GNNs compares favorably relative to several state-of-the-art baselines in both homophilic and heterophilic datasets, showcasing its promising potential.

Online Network Inference from Graph-Stationary Signals with Hidden Nodes

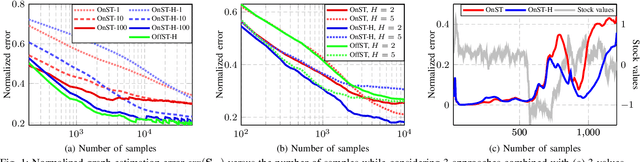
Graph learning is the fundamental task of estimating unknown graph connectivity from available data. Typical approaches assume that not only is all information available simultaneously but also that all nodes can be observed. However, in many real-world scenarios, data can neither be known completely nor obtained all at once. We present a novel method for online graph estimation that accounts for the presence of hidden nodes. We consider signals that are stationary on the underlying graph, which provides a model for the unknown connections to hidden nodes. We then formulate a convex optimization problem for graph learning from streaming, incomplete graph signals. We solve the proposed problem through an efficient proximal gradient algorithm that can run in real-time as data arrives sequentially. Additionally, we provide theoretical conditions under which our online algorithm is similar to batch-wise solutions. Through experimental results on synthetic and real-world data, we demonstrate the viability of our approach for online graph learning in the presence of missing observations.

Non-negative Weighted DAG Structure Learning

We address the problem of learning the topology of directed acyclic graphs (DAGs) from nodal observations, which adhere to a linear structural equation model. Recent advances framed the combinatorial DAG structure learning task as a continuous optimization problem, yet existing methods must contend with the complexities of non-convex optimization. To overcome this limitation, we assume that the latent DAG contains only non-negative edge weights. Leveraging this additional structure, we argue that cycles can be effectively characterized (and prevented) using a convex acyclicity function based on the log-determinant of the adjacency matrix. This convexity allows us to relax the task of learning the non-negative weighted DAG as an abstract convex optimization problem. We propose a DAG recovery algorithm based on the method of multipliers, that is guaranteed to return a global minimizer. Furthermore, we prove that in the infinite sample size regime, the convexity of our approach ensures the recovery of the true DAG structure. We empirically validate the performance of our algorithm in several reproducible synthetic-data test cases, showing that it outperforms state-of-the-art alternatives.

Fair GLASSO: Estimating Fair Graphical Models with Unbiased Statistical Behavior

We propose estimating Gaussian graphical models (GGMs) that are fair with respect to sensitive nodal attributes. Many real-world models exhibit unfair discriminatory behavior due to biases in data. Such discrimination is known to be exacerbated when data is equipped with pairwise relationships encoded in a graph. Additionally, the effect of biased data on graphical models is largely underexplored. We thus introduce fairness for graphical models in the form of two bias metrics to promote balance in statistical similarities across nodal groups with different sensitive attributes. Leveraging these metrics, we present Fair GLASSO, a regularized graphical lasso approach to obtain sparse Gaussian precision matrices with unbiased statistical dependencies across groups. We also propose an efficient proximal gradient algorithm to obtain the estimates. Theoretically, we express the tradeoff between fair and accurate estimated precision matrices. Critically, this includes demonstrating when accuracy can be preserved in the presence of a fairness regularizer. On top of this, we study the complexity of Fair GLASSO and demonstrate that our algorithm enjoys a fast convergence rate. Our empirical validation includes synthetic and real-world simulations that illustrate the value and effectiveness of our proposed optimization problem and iterative algorithm.