An index of effective number of variables for uncertainty and reliability analysis in model selection problems

An index of an effective number of variables (ENV) is introduced for model selection in nested models. This is the case, for instance, when we have to decide the order of a polynomial function or the number of bases in a nonlinear regression, choose the number of clusters in a clustering problem, or the number of features in a variable selection application (to name few examples). It is inspired by the idea of the maximum area under the curve (AUC). The interpretation of the ENV index is identical to the effective sample size (ESS) indices concerning a set of samples. The ENV index improves {drawbacks of} the elbow detectors described in the literature and introduces different confidence measures of the proposed solution. These novel measures can be also employed jointly with the use of different information criteria, such as the well-known AIC and BIC, or any other model selection procedures. Comparisons with classical and recent schemes are provided in different experiments involving real datasets. Related Matlab code is given.

Enhancing Graphical Lasso: A Robust Scheme for Non-Stationary Mean Data

This work addresses the problem of graph learning from data following a Gaussian Graphical Model (GGM) with a time-varying mean. Graphical Lasso (GL), the standard method for estimating sparse precision matrices, assumes that the observed data follows a zero-mean Gaussian distribution. However, this assumption is often violated in real-world scenarios where the mean evolves over time due to external influences, trends, or regime shifts. When the mean is not properly accounted for, applying GL directly can lead to estimating a biased precision matrix, hence hindering the graph learning task. To overcome this limitation, we propose Graphical Lasso with Adaptive Targeted Adaptive Importance Sampling (GL-ATAIS), an iterative method that jointly estimates the time-varying mean and the precision matrix. Our approach integrates Bayesian inference with frequentist estimation, leveraging importance sampling to obtain an estimate of the mean while using a regularized maximum likelihood estimator to infer the precision matrix. By iteratively refining both estimates, GL-ATAIS mitigates the bias introduced by time-varying means, leading to more accurate graph recovery. Our numerical evaluation demonstrates the impact of properly accounting for time-dependent means and highlights the advantages of GL-ATAIS over standard GL in recovering the true graph structure.

Optimality in importance sampling: a gentle survey

The performance of the Monte Carlo sampling methods relies on the crucial choice of a proposal density. The notion of optimality is fundamental to design suitable adaptive procedures of the proposal density within Monte Carlo schemes. This work is an exhaustive review around the concept of optimality in importance sampling. Several frameworks are described and analyzed, such as the marginal likelihood approximation for model selection, the use of multiple proposal densities, a sequence of tempered posteriors, and noisy scenarios including the applications to approximate Bayesian computation (ABC) and reinforcement learning, to name a few. Some theoretical and empirical comparisons are also provided.

CAMEO: Curiosity Augmented Metropolis for Exploratory Optimal Policies

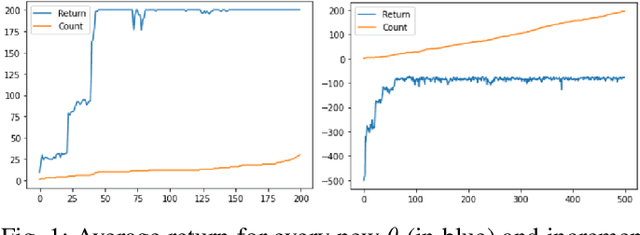
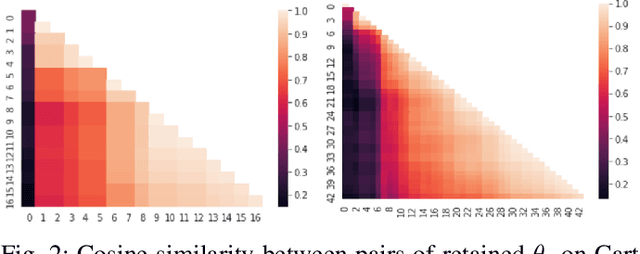
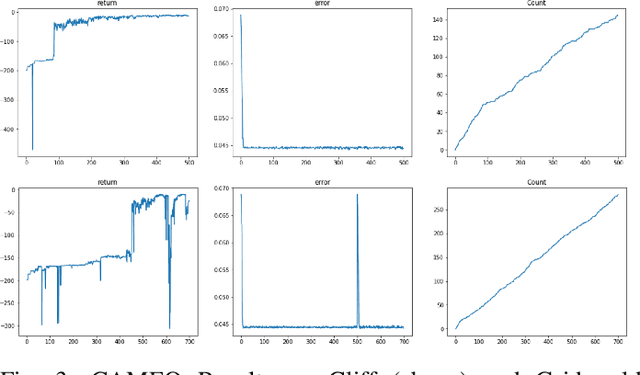
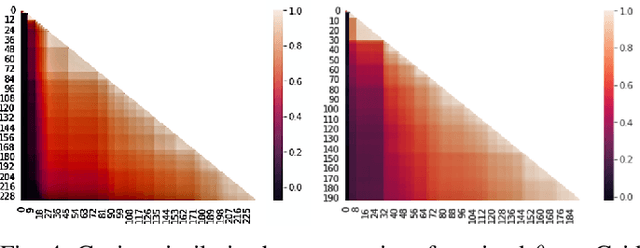
Reinforcement Learning has drawn huge interest as a tool for solving optimal control problems. Solving a given problem (task or environment) involves converging towards an optimal policy. However, there might exist multiple optimal policies that can dramatically differ in their behaviour; for example, some may be faster than the others but at the expense of greater risk. We consider and study a distribution of optimal policies. We design a curiosity-augmented Metropolis algorithm (CAMEO), such that we can sample optimal policies, and such that these policies effectively adopt diverse behaviours, since this implies greater coverage of the different possible optimal policies. In experimental simulations we show that CAMEO indeed obtains policies that all solve classic control problems, and even in the challenging case of environments that provide sparse rewards. We further show that the different policies we sample present different risk profiles, corresponding to interesting practical applications in interpretability, and represents a first step towards learning the distribution of optimal policies itself.

Inference over radiative transfer models using variational and expectation maximization methods

Earth observation from satellites offers the possibility to monitor our planet with unprecedented accuracy. Radiative transfer models (RTMs) encode the energy transfer through the atmosphere, and are used to model and understand the Earth system, as well as to estimate the parameters that describe the status of the Earth from satellite observations by inverse modeling. However, performing inference over such simulators is a challenging problem. RTMs are nonlinear, non-differentiable and computationally costly codes, which adds a high level of difficulty in inference. In this paper, we introduce two computational techniques to infer not only point estimates of biophysical parameters but also their joint distribution. One of them is based on a variational autoencoder approach and the second one is based on a Monte Carlo Expectation Maximization (MCEM) scheme. We compare and discuss benefits and drawbacks of each approach. We also provide numerical comparisons in synthetic simulations and the real PROSAIL model, a popular RTM that combines land vegetation leaf and canopy modeling. We analyze the performance of the two approaches for modeling and inferring the distribution of three key biophysical parameters for quantifying the terrestrial biosphere.

Optimality in Noisy Importance Sampling

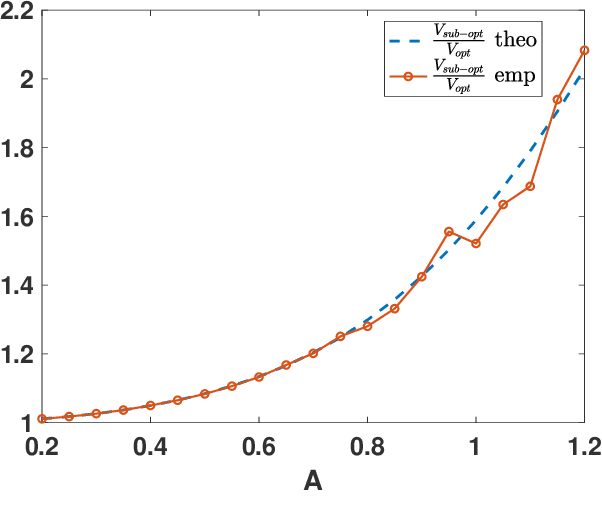
In this work, we analyze the noisy importance sampling (IS), i.e., IS working with noisy evaluations of the target density. We present the general framework and derive optimal proposal densities for noisy IS estimators. The optimal proposals incorporate the information of the variance of the noisy realizations, proposing points in regions where the noise power is higher. We also compare the use of the optimal proposals with previous optimality approaches considered in a noisy IS framework.

Compressed particle methods for expensive models with application in Astronomy and Remote Sensing

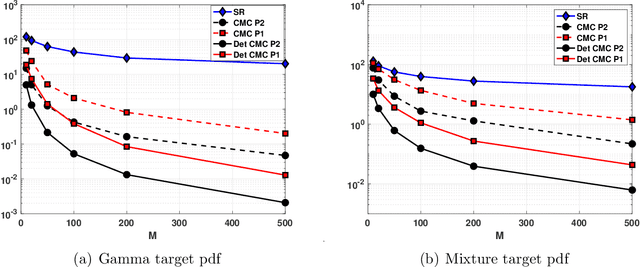
In many inference problems, the evaluation of complex and costly models is often required. In this context, Bayesian methods have become very popular in several fields over the last years, in order to obtain parameter inversion, model selection or uncertainty quantification. Bayesian inference requires the approximation of complicated integrals involving (often costly) posterior distributions. Generally, this approximation is obtained by means of Monte Carlo (MC) methods. In order to reduce the computational cost of the corresponding technique, surrogate models (also called emulators) are often employed. Another alternative approach is the so-called Approximate Bayesian Computation (ABC) scheme. ABC does not require the evaluation of the costly model but the ability to simulate artificial data according to that model. Moreover, in ABC, the choice of a suitable distance between real and artificial data is also required. In this work, we introduce a novel approach where the expensive model is evaluated only in some well-chosen samples. The selection of these nodes is based on the so-called compressed Monte Carlo (CMC) scheme. We provide theoretical results supporting the novel algorithms and give empirical evidence of the performance of the proposed method in several numerical experiments. Two of them are real-world applications in astronomy and satellite remote sensing.

Compressed Monte Carlo with application in particle filtering

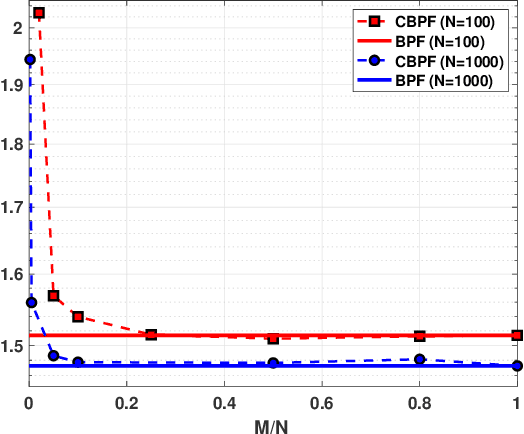
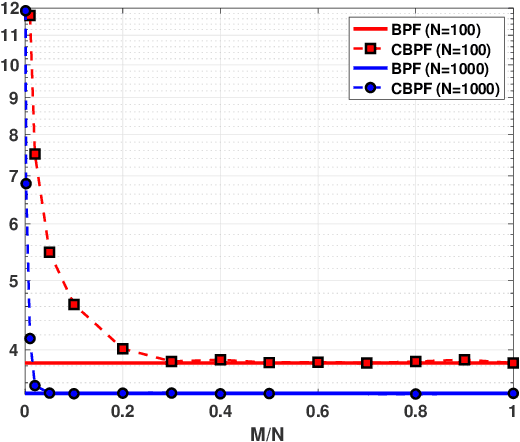
Bayesian models have become very popular over the last years in several fields such as signal processing, statistics, and machine learning. Bayesian inference requires the approximation of complicated integrals involving posterior distributions. For this purpose, Monte Carlo (MC) methods, such as Markov Chain Monte Carlo and importance sampling algorithms, are often employed. In this work, we introduce the theory and practice of a Compressed MC (C-MC) scheme to compress the statistical information contained in a set of random samples. In its basic version, C-MC is strictly related to the stratification technique, a well-known method used for variance reduction purposes. Deterministic C-MC schemes are also presented, which provide very good performance. The compression problem is strictly related to the moment matching approach applied in different filtering techniques, usually called as Gaussian quadrature rules or sigma-point methods. C-MC can be employed in a distributed Bayesian inference framework when cheap and fast communications with a central processor are required. Furthermore, C-MC is useful within particle filtering and adaptive IS algorithms, as shown by three novel schemes introduced in this work. Six numerical results confirm the benefits of the introduced schemes, outperforming the corresponding benchmark methods. A related code is also provided.

Integrating Domain Knowledge in Data-driven Earth Observation with Process Convolutions

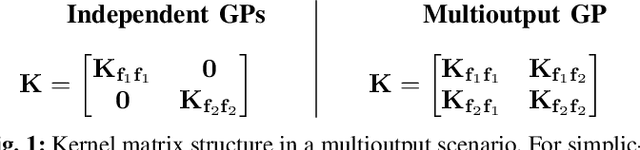
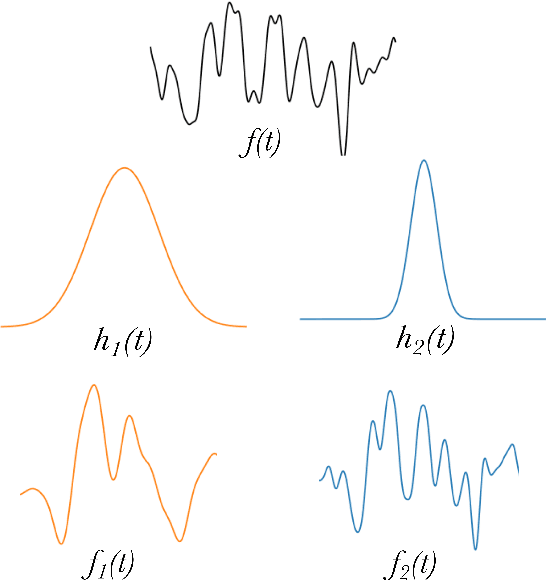
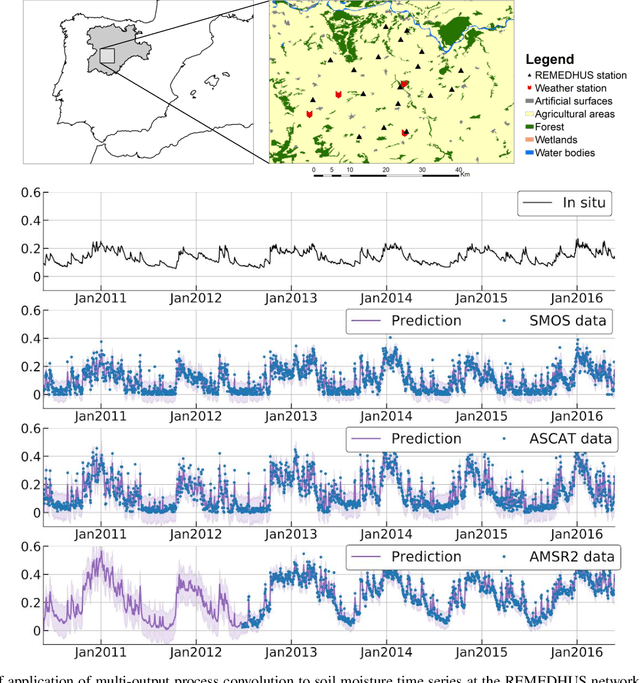
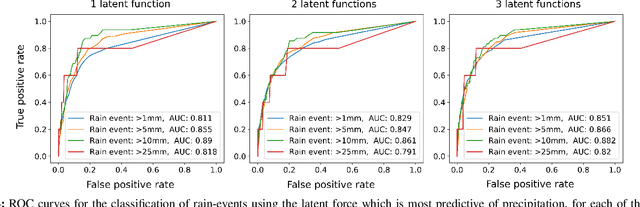
The modelling of Earth observation data is a challenging problem, typically approached by either purely mechanistic or purely data-driven methods. Mechanistic models encode the domain knowledge and physical rules governing the system. Such models, however, need the correct specification of all interactions between variables in the problem and the appropriate parameterization is a challenge in itself. On the other hand, machine learning approaches are flexible data-driven tools, able to approximate arbitrarily complex functions, but lack interpretability and struggle when data is scarce or in extrapolation regimes. In this paper, we argue that hybrid learning schemes that combine both approaches can address all these issues efficiently. We introduce Gaussian process (GP) convolution models for hybrid modelling in Earth observation (EO) problems. We specifically propose the use of a class of GP convolution models called latent force models (LFMs) for EO time series modelling, analysis and understanding. LFMs are hybrid models that incorporate physical knowledge encoded in differential equations into a multioutput GP model. LFMs can transfer information across time-series, cope with missing observations, infer explicit latent functions forcing the system, and learn parameterizations which are very helpful for system analysis and interpretability. We consider time series of soil moisture from active (ASCAT) and passive (SMOS, AMSR2) microwave satellites. We show how assuming a first order differential equation as governing equation, the model automatically estimates the e-folding time or decay rate related to soil moisture persistence and discovers latent forces related to precipitation. The proposed hybrid methodology reconciles the two main approaches in remote sensing parameter estimation by blending statistical learning and mechanistic modeling.

Living in the Physics and Machine Learning Interplay for Earth Observation

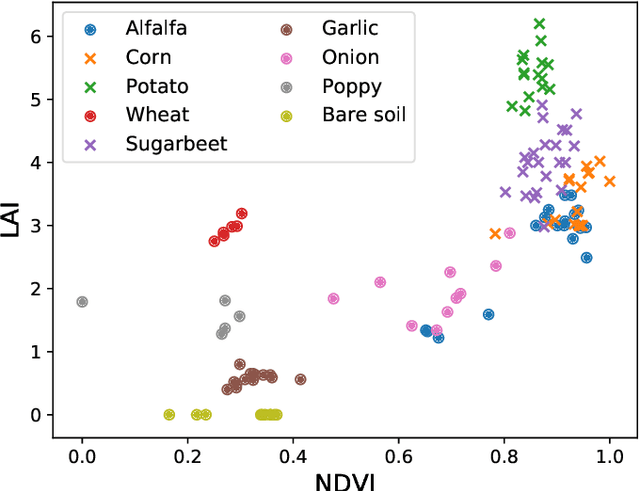
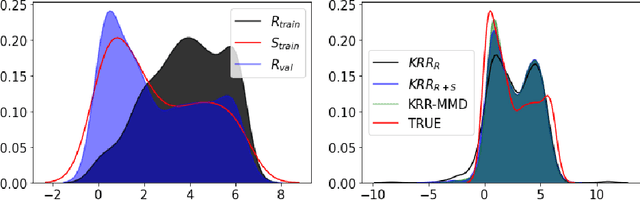
Most problems in Earth sciences aim to do inferences about the system, where accurate predictions are just a tiny part of the whole problem. Inferences mean understanding variables relations, deriving models that are physically interpretable, that are simple parsimonious, and mathematically tractable. Machine learning models alone are excellent approximators, but very often do not respect the most elementary laws of physics, like mass or energy conservation, so consistency and confidence are compromised. In this paper, we describe the main challenges ahead in the field, and introduce several ways to live in the Physics and machine learning interplay: to encode differential equations from data, constrain data-driven models with physics-priors and dependence constraints, improve parameterizations, emulate physical models, and blend data-driven and process-based models. This is a collective long-term AI agenda towards developing and applying algorithms capable of discovering knowledge in the Earth system.