Integrating Domain Knowledge in Data-driven Earth Observation with Process Convolutions

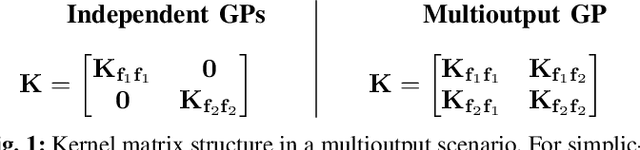
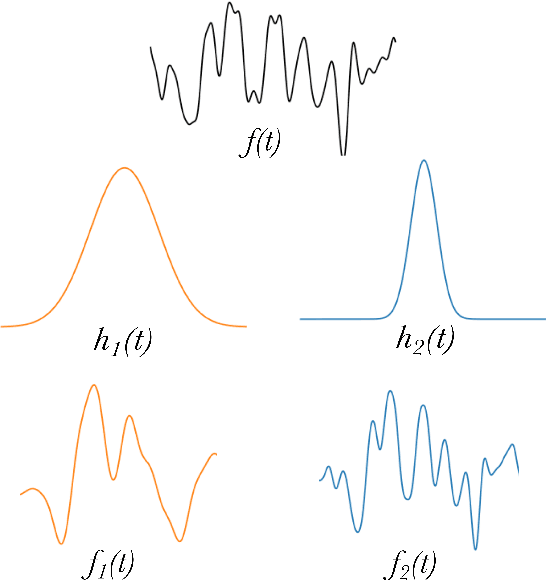
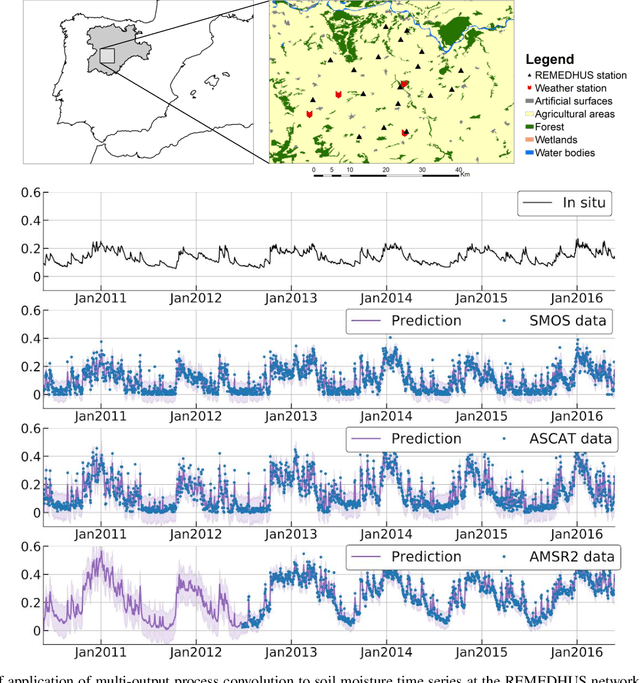
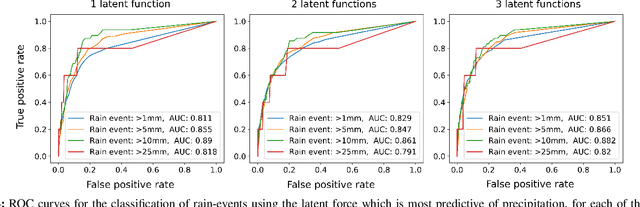
The modelling of Earth observation data is a challenging problem, typically approached by either purely mechanistic or purely data-driven methods. Mechanistic models encode the domain knowledge and physical rules governing the system. Such models, however, need the correct specification of all interactions between variables in the problem and the appropriate parameterization is a challenge in itself. On the other hand, machine learning approaches are flexible data-driven tools, able to approximate arbitrarily complex functions, but lack interpretability and struggle when data is scarce or in extrapolation regimes. In this paper, we argue that hybrid learning schemes that combine both approaches can address all these issues efficiently. We introduce Gaussian process (GP) convolution models for hybrid modelling in Earth observation (EO) problems. We specifically propose the use of a class of GP convolution models called latent force models (LFMs) for EO time series modelling, analysis and understanding. LFMs are hybrid models that incorporate physical knowledge encoded in differential equations into a multioutput GP model. LFMs can transfer information across time-series, cope with missing observations, infer explicit latent functions forcing the system, and learn parameterizations which are very helpful for system analysis and interpretability. We consider time series of soil moisture from active (ASCAT) and passive (SMOS, AMSR2) microwave satellites. We show how assuming a first order differential equation as governing equation, the model automatically estimates the e-folding time or decay rate related to soil moisture persistence and discovers latent forces related to precipitation. The proposed hybrid methodology reconciles the two main approaches in remote sensing parameter estimation by blending statistical learning and mechanistic modeling.

Efficient Monte Carlo Methods for Multi-Dimensional Learning with Classifier Chains

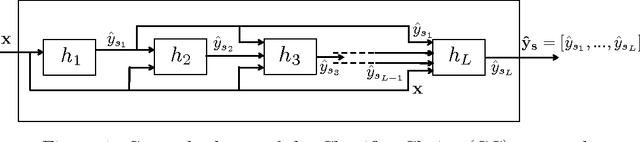
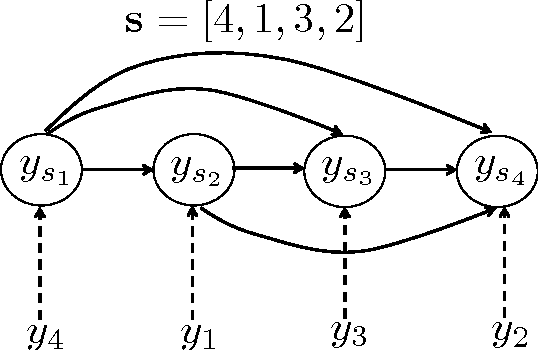
Multi-dimensional classification (MDC) is the supervised learning problem where an instance is associated with multiple classes, rather than with a single class, as in traditional classification problems. Since these classes are often strongly correlated, modeling the dependencies between them allows MDC methods to improve their performance - at the expense of an increased computational cost. In this paper we focus on the classifier chains (CC) approach for modeling dependencies, one of the most popular and highest- performing methods for multi-label classification (MLC), a particular case of MDC which involves only binary classes (i.e., labels). The original CC algorithm makes a greedy approximation, and is fast but tends to propagate errors along the chain. Here we present novel Monte Carlo schemes, both for finding a good chain sequence and performing efficient inference. Our algorithms remain tractable for high-dimensional data sets and obtain the best predictive performance across several real data sets.

Blind Analysis of EGM Signals: Sparsity-Aware Formulation

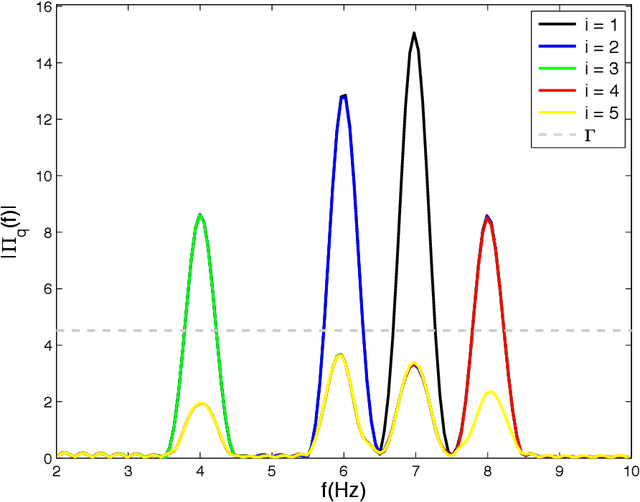
This technical note considers the problems of blind sparse learning and inference of electrogram (EGM) signals under atrial fibrillation (AF) conditions. First of all we introduce a mathematical model for the observed signals that takes into account the multiple foci typically appearing inside the heart during AF. Then we propose a reconstruction model based on a fixed dictionary and discuss several alternatives for choosing the dictionary. In order to obtain a sparse solution that takes into account the biological restrictions of the problem, a first alternative is using LASSO regularization followed by a post-processing stage that removes low amplitude coefficients violating the refractory period characteristic of cardiac cells. As an alternative we propose a novel regularization term, called cross products LASSO (CP-LASSO), that is able to incorporate the biological constraints directly into the optimization problem. Unfortunately, the resulting problem is non-convex, but we show how it can be solved efficiently in an approximated way making use of successive convex approximations (SCA). Finally, spectral analysis is performed on the clean activation sequence obtained from the sparse learning stage in order to estimate the number of latent foci and their frequencies. Simulations on synthetic and real data are provided to validate the proposed approach.

Linear Latent Force Models using Gaussian Processes

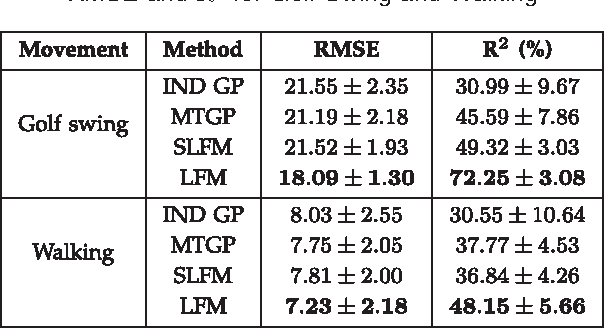
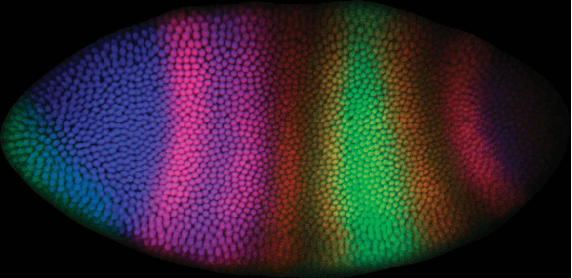
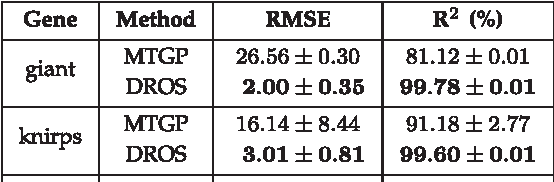
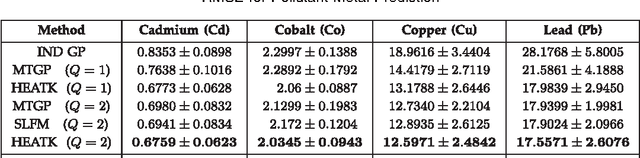
Purely data driven approaches for machine learning present difficulties when data is scarce relative to the complexity of the model or when the model is forced to extrapolate. On the other hand, purely mechanistic approaches need to identify and specify all the interactions in the problem at hand (which may not be feasible) and still leave the issue of how to parameterize the system. In this paper, we present a hybrid approach using Gaussian processes and differential equations to combine data driven modelling with a physical model of the system. We show how different, physically-inspired, kernel functions can be developed through sensible, simple, mechanistic assumptions about the underlying system. The versatility of our approach is illustrated with three case studies from motion capture, computational biology and geostatistics.

Variational Inducing Kernels for Sparse Convolved Multiple Output Gaussian Processes

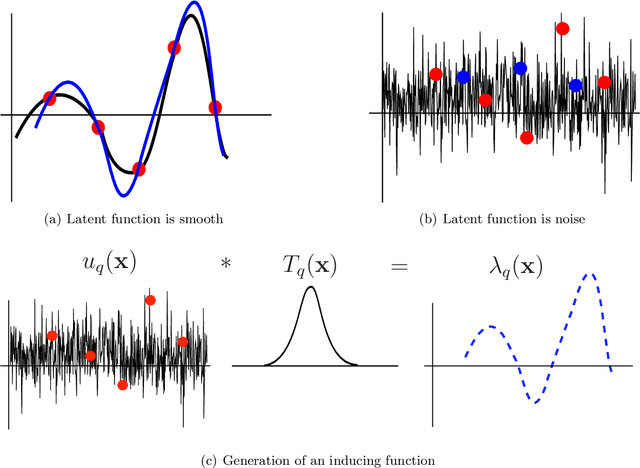
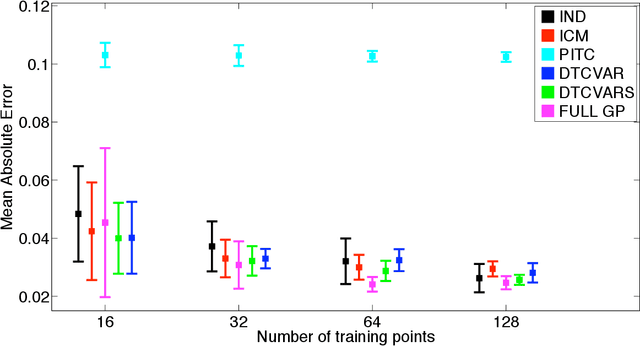
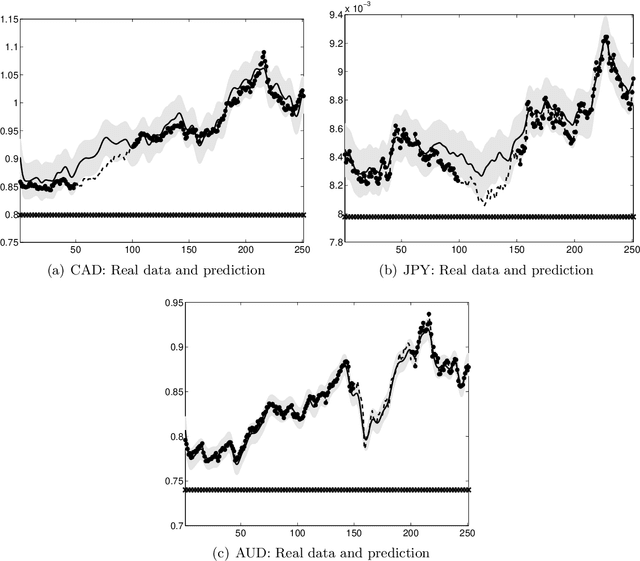
Interest in multioutput kernel methods is increasing, whether under the guise of multitask learning, multisensor networks or structured output data. From the Gaussian process perspective a multioutput Mercer kernel is a covariance function over correlated output functions. One way of constructing such kernels is based on convolution processes (CP). A key problem for this approach is efficient inference. Alvarez and Lawrence (2009) recently presented a sparse approximation for CPs that enabled efficient inference. In this paper, we extend this work in two directions: we introduce the concept of variational inducing functions to handle potential non-smooth functions involved in the kernel CP construction and we consider an alternative approach to approximate inference based on variational methods, extending the work by Titsias (2009) to the multiple output case. We demonstrate our approaches on prediction of school marks, compiler performance and financial time series.