Adaptive RKHS Fourier Features for Compositional Gaussian Process Models

Deep Gaussian Processes (DGPs) leverage a compositional structure to model non-stationary processes. DGPs typically rely on local inducing point approximations across intermediate GP layers. Recent advances in DGP inference have shown that incorporating global Fourier features from Reproducing Kernel Hilbert Space (RKHS) can enhance the DGPs' capability to capture complex non-stationary patterns. This paper extends the use of these features to compositional GPs involving linear transformations. In particular, we introduce Ordinary Differential Equation (ODE) -based RKHS Fourier features that allow for adaptive amplitude and phase modulation through convolution operations. This convolutional formulation relates our work to recently proposed deep latent force models, a multi-layer structure designed for modelling nonlinear dynamical systems. By embedding these adjustable RKHS Fourier features within a doubly stochastic variational inference framework, our model exhibits improved predictive performance across various regression tasks.

Deep Latent Force Models: ODE-based Process Convolutions for Bayesian Deep Learning

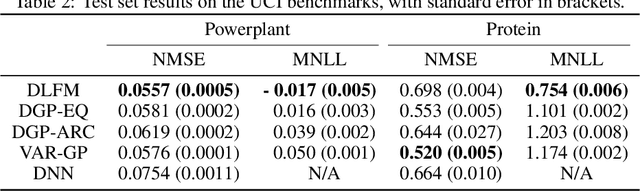
Effectively modeling phenomena present in highly nonlinear dynamical systems whilst also accurately quantifying uncertainty is a challenging task, which often requires problem-specific techniques. We outline the deep latent force model (DLFM), a domain-agnostic approach to tackling this problem, which consists of a deep Gaussian process architecture where the kernel at each layer is derived from an ordinary differential equation using the framework of process convolutions. Two distinct formulations of the DLFM are presented which utilise weight-space and variational inducing points-based Gaussian process approximations, both of which are amenable to doubly stochastic variational inference. We provide evidence that our model is capable of capturing highly nonlinear behaviour in real-world multivariate time series data. In addition, we find that our approach achieves comparable performance to a number of other probabilistic models on benchmark regression tasks. We also empirically assess the negative impact of the inducing points framework on the extrapolation capabilities of LFM-based models.

Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.

Shallow and Deep Nonparametric Convolutions for Gaussian Processes

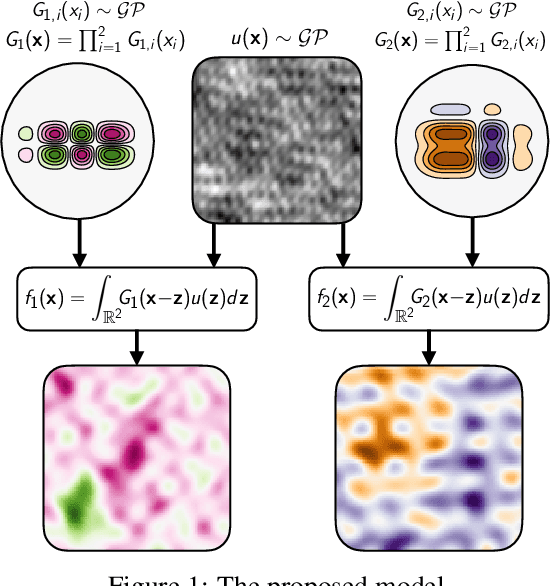
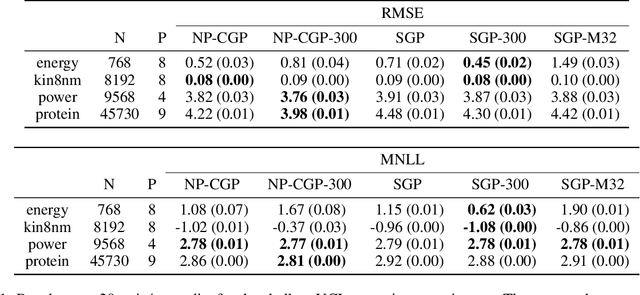
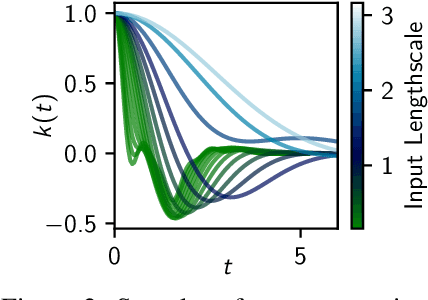
A key challenge in the practical application of Gaussian processes (GPs) is selecting a proper covariance function. The moving average, or process convolutions, construction of GPs allows some additional flexibility, but still requires choosing a proper smoothing kernel, which is non-trivial. Previous approaches have built covariance functions by using GP priors over the smoothing kernel, and by extension the covariance, as a way to bypass the need to specify it in advance. However, such models have been limited in several ways: they are restricted to single dimensional inputs, e.g. time; they only allow modelling of single outputs and they do not scale to large datasets since inference is not straightforward. In this paper, we introduce a nonparametric process convolution formulation for GPs that alleviates these weaknesses by using a functional sampling approach based on Matheron's rule to perform fast sampling using interdomain inducing variables. Furthermore, we propose a composition of these nonparametric convolutions that serves as an alternative to classic deep GP models, and allows the covariance functions of the intermediate layers to be inferred from the data. We test the performance of our model on benchmarks for single output GPs, multiple output GPs and deep GPs and find that in many cases our approach can provide improvements over standard GP models.

Angular Super-Resolution in Diffusion MRI with a 3D Recurrent Convolutional Autoencoder

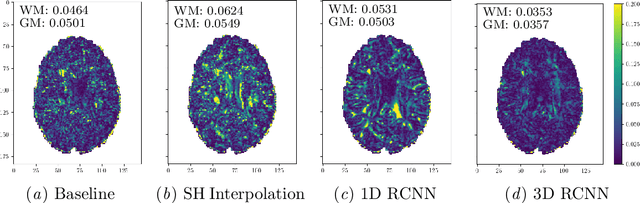
High resolution diffusion MRI (dMRI) data is often constrained by limited scanning time in clinical settings, thus restricting the use of downstream analysis techniques that would otherwise be available. In this work we develop a 3D recurrent convolutional neural network (RCNN) capable of super-resolving dMRI volumes in the angular (q-space) domain. Our approach formulates the task of angular super-resolution as a patch-wise regression using a 3D autoencoder conditioned on target b-vectors. Within the network we use a convolutional long short term memory (ConvLSTM) cell to model the relationship between q-space samples. We compare model performance against a baseline spherical harmonic interpolation and a 1D variant of the model architecture. We show that the 3D model has the lowest error rates across different subsampling schemes and b-values. The relative performance of the 3D RCNN is greatest in the very low angular resolution domain. Code for this project is available at https://github.com/m-lyon/dMRI-RCNN.

Modular Gaussian Processes for Transfer Learning

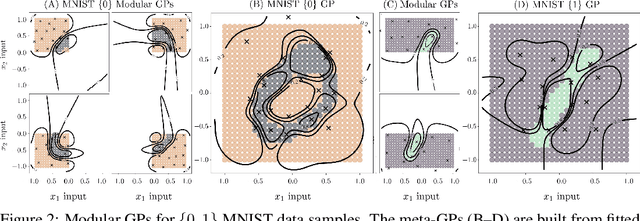
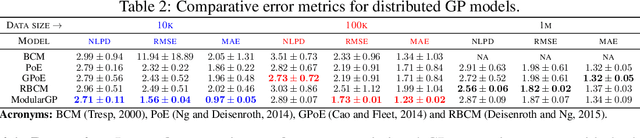
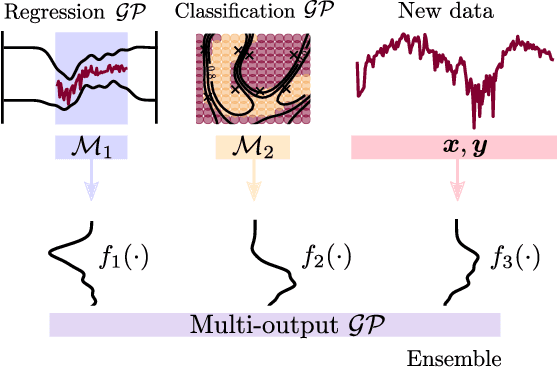
We present a framework for transfer learning based on modular variational Gaussian processes (GP). We develop a module-based method that having a dictionary of well fitted GPs, one could build ensemble GP models without revisiting any data. Each model is characterised by its hyperparameters, pseudo-inputs and their corresponding posterior densities. Our method avoids undesired data centralisation, reduces rising computational costs and allows the transfer of learned uncertainty metrics after training. We exploit the augmentation of high-dimensional integral operators based on the Kullback-Leibler divergence between stochastic processes to introduce an efficient lower bound under all the sparse variational GPs, with different complexity and even likelihood distribution. The method is also valid for multi-output GPs, learning correlations a posteriori between independent modules. Extensive results illustrate the usability of our framework in large-scale and multi-task experiments, also compared with the exact inference methods in the literature.

Compositional Modeling of Nonlinear Dynamical Systems with ODE-based Random Features

Effectively modeling phenomena present in highly nonlinear dynamical systems whilst also accurately quantifying uncertainty is a challenging task, which often requires problem-specific techniques. We present a novel, domain-agnostic approach to tackling this problem, using compositions of physics-informed random features, derived from ordinary differential equations. The architecture of our model leverages recent advances in approximate inference for deep Gaussian processes, such as layer-wise weight-space approximations which allow us to incorporate random Fourier features, and stochastic variational inference for approximate Bayesian inference. We provide evidence that our model is capable of capturing highly nonlinear behaviour in real-world multivariate time series data. In addition, we find that our approach achieves comparable performance to a number of other probabilistic models on benchmark regression tasks.

Learning Nonparametric Volterra Kernels with Gaussian Processes

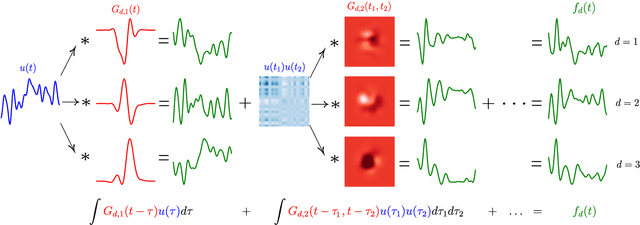
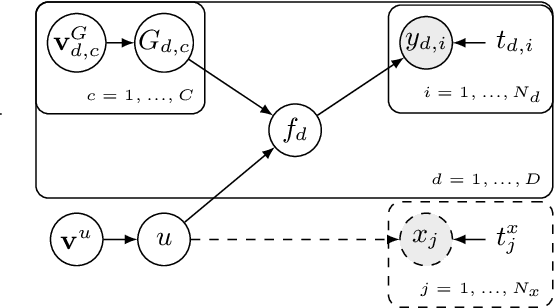
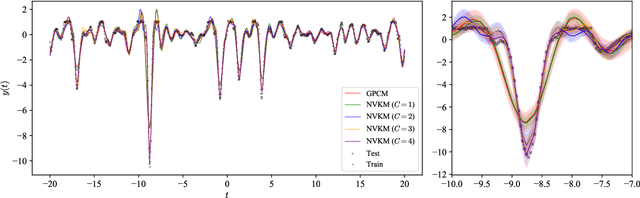
This paper introduces a method for the nonparametric Bayesian learning of nonlinear operators, through the use of the Volterra series with kernels represented using Gaussian processes (GPs), which we term the nonparametric Volterra kernels model (NVKM). When the input function to the operator is unobserved and has a GP prior, the NVKM constitutes a powerful method for both single and multiple output regression, and can be viewed as a nonlinear and nonparametric latent force model. When the input function is observed, the NVKM can be used to perform Bayesian system identification. We use recent advances in efficient sampling of explicit functions from GPs to map process realisations through the Volterra series without resorting to numerical integration, allowing scalability through doubly stochastic variational inference, and avoiding the need for Gaussian approximations of the output processes. We demonstrate the performance of the model for both multiple output regression and system identification using standard benchmarks.

Recyclable Gaussian Processes

We present a new framework for recycling independent variational approximations to Gaussian processes. The main contribution is the construction of variational ensembles given a dictionary of fitted Gaussian processes without revisiting any subset of observations. Our framework allows for regression, classification and heterogeneous tasks, i.e. mix of continuous and discrete variables over the same input domain. We exploit infinite-dimensional integral operators based on the Kullback-Leibler divergence between stochastic processes to re-combine arbitrary amounts of variational sparse approximations with different complexity, likelihood model and location of the pseudo-inputs. Extensive results illustrate the usability of our framework in large-scale distributed experiments, also compared with the exact inference models in the literature.

A Fully Natural Gradient Scheme for Improving Inference of the Heterogeneous Multi-Output Gaussian Process Model

A recent novel extension of multi-output Gaussian processes handles heterogeneous outputs assuming that each output has its own likelihood function. It uses a vector-valued Gaussian process prior to jointly model all likelihoods' parameters as latent functions drawn from a Gaussian process with a linear model of coregionalisation covariance. By means of an inducing points framework, the model is able to obtain tractable variational bounds amenable to stochastic variational inference. Nonetheless, the strong conditioning between the variational parameters and the hyper-parameters burdens the adaptive gradient optimisation methods used in the original approach. To overcome this issue we borrow ideas from variational optimisation introducing an exploratory distribution over the hyper-parameters, allowing inference together with the variational parameters through a fully natural gradient optimisation scheme. We show that our optimisation scheme can achieve better local optima solution with higher test performance rates than adaptive gradient methods or an hybrid strategy that partially use natural gradients in cooperation with the Adam method. We compare the performance of the different methods over toy and real databases.