Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.

Minimal Learning Machine for Multi-Label Learning

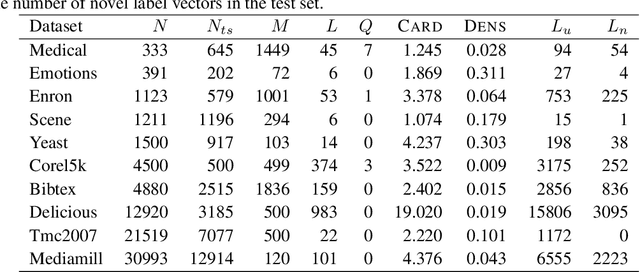
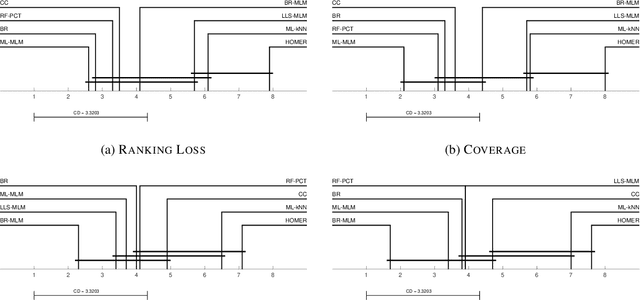
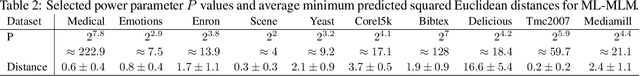
Distance-based supervised method, the minimal learning machine, constructs a predictive model from data by learning a mapping between input and output distance matrices. In this paper, we propose methods and evaluate how this technique and its core component, the distance mapping, can be adapted to multi-label learning. The proposed approach is based on combining the distance mapping with an inverse distance weighting. Although the proposal is one of the simplest methods in the multi-label learning literature, it achieves state-of-the-art performance for small to moderate-sized multi-label learning problems. Besides its simplicity, the proposed method is fully deterministic and its hyper-parameter can be selected via ranking loss-based statistic which has a closed form, thus avoiding conventional cross-validation-based hyper-parameter tuning. In addition, due to its simple linear distance mapping-based construction, we demonstrate that the proposed method can assess predictions' uncertainty for multi-label classification, which is a valuable capability for data-centric machine learning pipelines.

Minimal Learning Machine: Theoretical Results and Clustering-Based Reference Point Selection

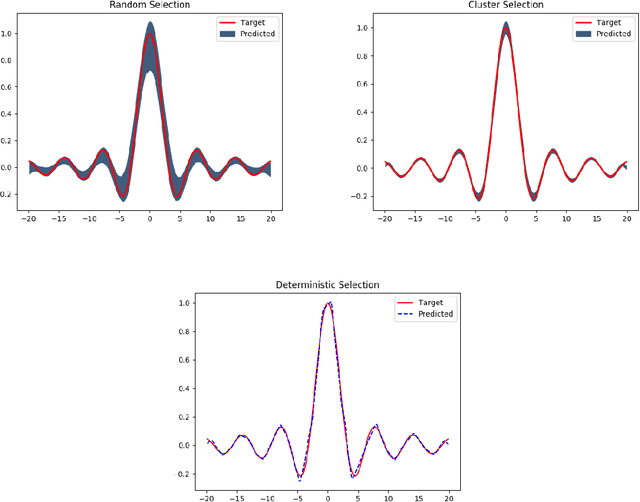
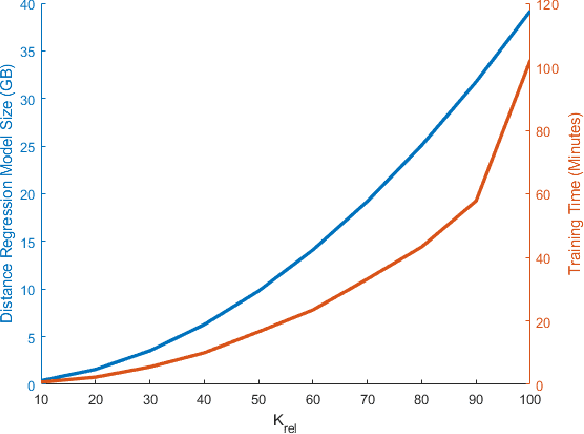
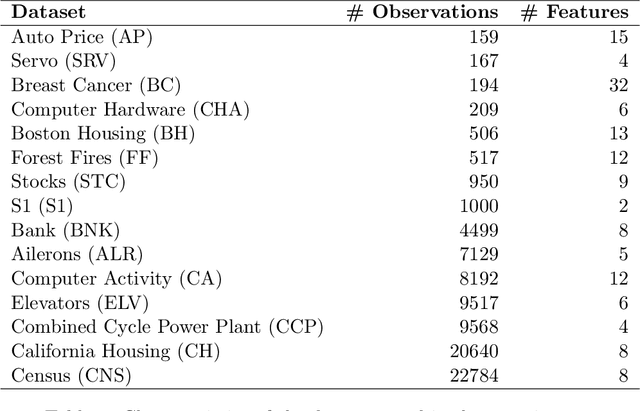
The Minimal Learning Machine (MLM) is a nonlinear supervised approach based on learning a linear mapping between distance matrices computed in the input and output data spaces, where distances are calculated concerning a subset of points called reference points. Its simple formulation has attracted several recent works on extensions and applications. In this paper, we aim to address some open questions related to the MLM. First, we detail theoretical aspects that assure the interpolation and universal approximation capabilities of the MLM, which were previously only empirically verified. Second, we identify the task of selecting reference points as having major importance for the MLM's generalization capability; furthermore, we assess several clustering-based methods in regression scenarios. Based on an extensive empirical evaluation, we conclude that the evaluated methods are both scalable and useful. Specifically, for a small number of reference points, the clustering-based methods outperformed the standard random selection of the original MLM formulation.

No-PASt-BO: Normalized Portfolio Allocation Strategy for Bayesian Optimization

Bayesian Optimization (BO) is a framework for black-box optimization that is especially suitable for expensive cost functions. Among the main parts of a BO algorithm, the acquisition function is of fundamental importance, since it guides the optimization algorithm by translating the uncertainty of the regression model in a utility measure for each point to be evaluated. Considering such aspect, selection and design of acquisition functions are one of the most popular research topics in BO. Since no single acquisition function was proved to have better performance in all tasks, a well-established approach consists of selecting different acquisition functions along the iterations of a BO execution. In such an approach, the GP-Hedge algorithm is a widely used option given its simplicity and good performance. Despite its success in various applications, GP-Hedge shows an undesirable characteristic of accounting on all past performance measures of each acquisition function to select the next function to be used. In this case, good or bad values obtained in an initial iteration may impact the choice of the acquisition function for the rest of the algorithm. This fact may induce a dominant behavior of an acquisition function and impact the final performance of the method. Aiming to overcome such limitation, in this work we propose a variant of GP-Hedge, named No-PASt-BO, that reduce the influence of far past evaluations. Moreover, our method presents a built-in normalization that avoids the functions in the portfolio to have similar probabilities, thus improving the exploration. The obtained results on both synthetic and real-world optimization tasks indicate that No-PASt-BO presents competitive performance and always outperforms GP-Hedge.

LS-SVR as a Bayesian RBF network

We show the theoretical equivalence between the Least Squares Support Vector Regression (LS-SVR) model and maximum a posteriori (MAP) inference on Bayesian Radial Basis Functions (RBF) networks with a specific Gaussian prior on the regression weights. Although previous works have pointed out similar expressions between those learning approaches, we explicit and formally state such correspondence. We empirically demonstrate our result by performing computational experiments with standard regression benchmarks. Our findings open a range of possibilities to improve LS-SVR borrowing strength from well-established developments in Bayesian methodology.