Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.

Anomaly Detection in Trajectory Data with Normalizing Flows

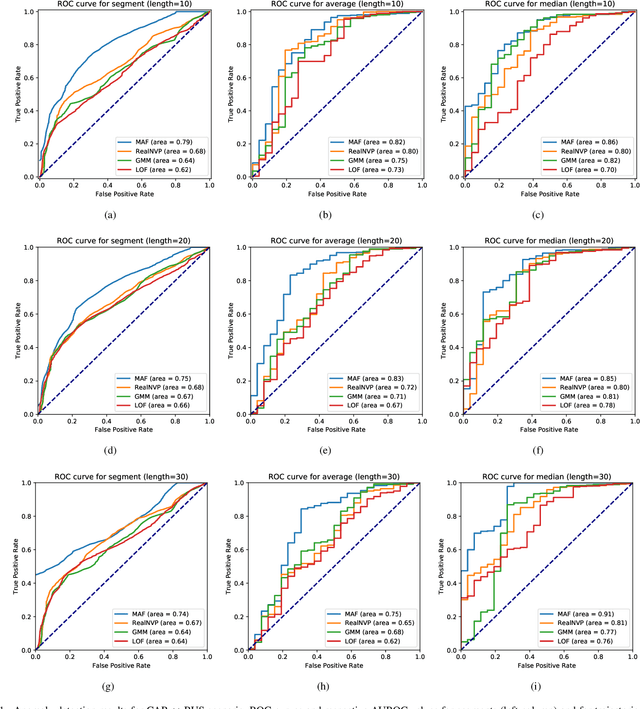
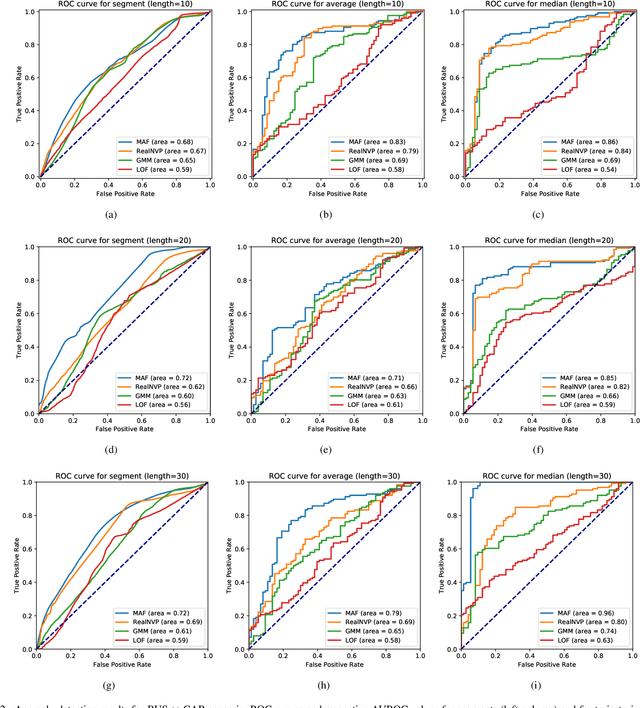
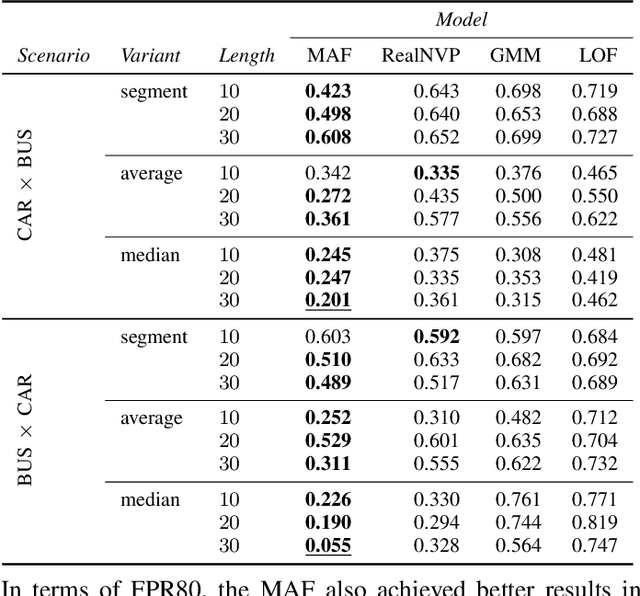
The task of detecting anomalous data patterns is as important in practical applications as challenging. In the context of spatial data, recognition of unexpected trajectories brings additional difficulties, such as high dimensionality and varying pattern lengths. We aim to tackle such a problem from a probability density estimation point of view, since it provides an unsupervised procedure to identify out of distribution samples. More specifically, we pursue an approach based on normalizing flows, a recent framework that enables complex density estimation from data with neural networks. Our proposal computes exact model likelihood values, an important feature of normalizing flows, for each segment of the trajectory. Then, we aggregate the segments' likelihoods into a single coherent trajectory anomaly score. Such a strategy enables handling possibly large sequences with different lengths. We evaluate our methodology, named aggregated anomaly detection with normalizing flows (GRADINGS), using real world trajectory data and compare it with more traditional anomaly detection techniques. The promising results obtained in the performed computational experiments indicate the feasibility of the GRADINGS, specially the variant that considers autoregressive normalizing flows.

Unscented Gaussian Process Latent Variable Model: learning from uncertain inputs with intractable kernels

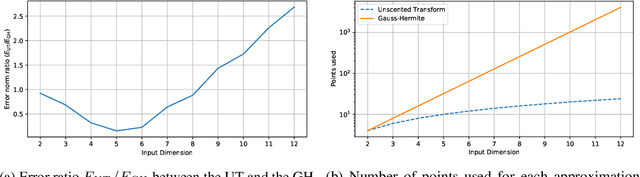
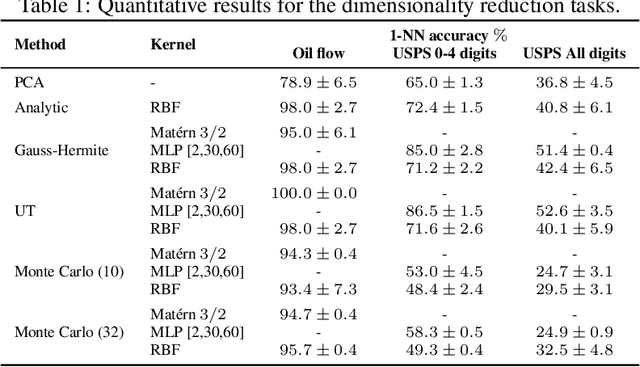
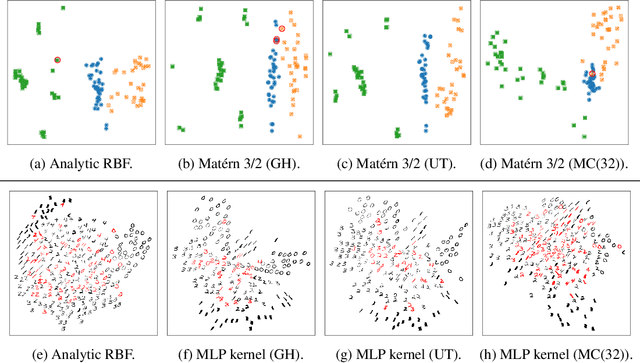
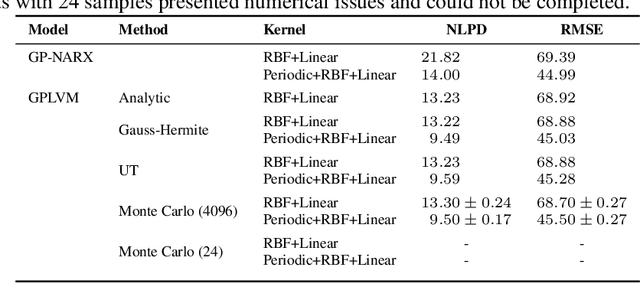
The Gaussian Process (GP) framework flexibility has enabled its use in several data modeling scenarios. The setting where we have unavailable or uncertain inputs that generate possibly noisy observations is usually tackled by the well known Gaussian Process Latent Variable Model (GPLVM). However, the standard variational approach to perform inference with the GPLVM presents some expressions that are tractable for only a few kernel functions, which may hinder its general application. While other quadrature or sampling approaches could be used in that case, they usually are very slow and/or non-deterministic. In the present paper, we propose the use of the unscented transformation to enable the use of any kernel function within the Bayesian GPLVM. Our approach maintains the fully deterministic feature of tractable kernels and presents a simple implementation with only moderate computational cost. Experiments on dimensionality reduction and multistep-ahead prediction with uncertainty propagation indicate the feasibility of our proposal.

Recurrent Gaussian Processes

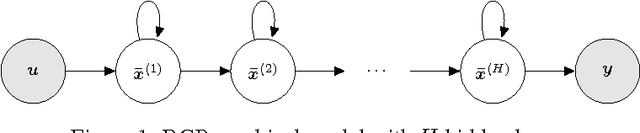
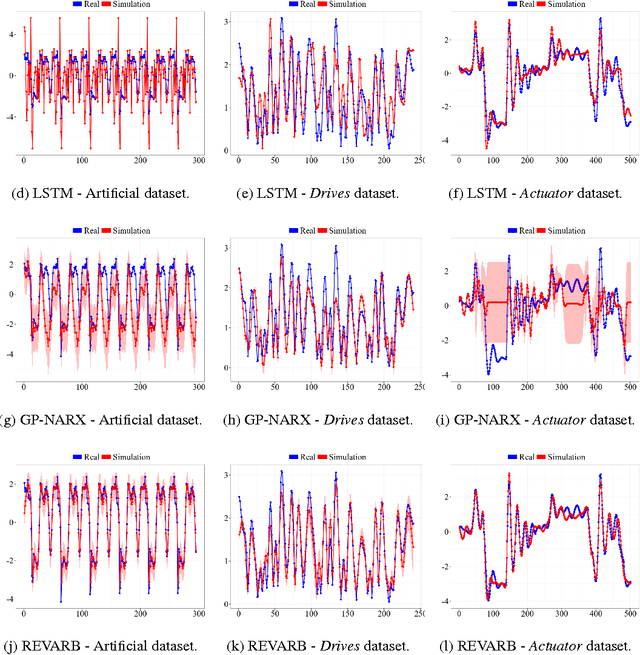
We define Recurrent Gaussian Processes (RGP) models, a general family of Bayesian nonparametric models with recurrent GP priors which are able to learn dynamical patterns from sequential data. Similar to Recurrent Neural Networks (RNNs), RGPs can have different formulations for their internal states, distinct inference methods and be extended with deep structures. In such context, we propose a novel deep RGP model whose autoregressive states are latent, thereby performing representation and dynamical learning simultaneously. To fully exploit the Bayesian nature of the RGP model we develop the Recurrent Variational Bayes (REVARB) framework, which enables efficient inference and strong regularization through coherent propagation of uncertainty across the RGP layers and states. We also introduce a RGP extension where variational parameters are greatly reduced by being reparametrized through RNN-based sequential recognition models. We apply our model to the tasks of nonlinear system identification and human motion modeling. The promising obtained results indicate that our RGP model maintains its highly flexibility while being able to avoid overfitting and being applicable even when larger datasets are not available.