Streaming Bayes GFlowNets

Bayes' rule naturally allows for inference refinement in a streaming fashion, without the need to recompute posteriors from scratch whenever new data arrives. In principle, Bayesian streaming is straightforward: we update our prior with the available data and use the resulting posterior as a prior when processing the next data chunk. In practice, however, this recipe entails i) approximating an intractable posterior at each time step; and ii) encapsulating results appropriately to allow for posterior propagation. For continuous state spaces, variational inference (VI) is particularly convenient due to its scalability and the tractability of variational posteriors. For discrete state spaces, however, state-of-the-art VI results in analytically intractable approximations that are ill-suited for streaming settings. To enable streaming Bayesian inference over discrete parameter spaces, we propose streaming Bayes GFlowNets (abbreviated as SB-GFlowNets) by leveraging the recently proposed GFlowNets -- a powerful class of amortized samplers for discrete compositional objects. Notably, SB-GFlowNet approximates the initial posterior using a standard GFlowNet and subsequently updates it using a tailored procedure that requires only the newly observed data. Our case studies in linear preference learning and phylogenetic inference showcase the effectiveness of SB-GFlowNets in sampling from an unnormalized posterior in a streaming setting. As expected, we also observe that SB-GFlowNets is significantly faster than repeatedly training a GFlowNet from scratch to sample from the full posterior.

On Divergence Measures for Training GFlowNets

Generative Flow Networks (GFlowNets) are amortized inference models designed to sample from unnormalized distributions over composable objects, with applications in generative modeling for tasks in fields such as causal discovery, NLP, and drug discovery. Traditionally, the training procedure for GFlowNets seeks to minimize the expected log-squared difference between a proposal (forward policy) and a target (backward policy) distribution, which enforces certain flow-matching conditions. While this training procedure is closely related to variational inference (VI), directly attempting standard Kullback-Leibler (KL) divergence minimization can lead to proven biased and potentially high-variance estimators. Therefore, we first review four divergence measures, namely, Renyi-$\alpha$'s, Tsallis-$\alpha$'s, reverse and forward KL's, and design statistically efficient estimators for their stochastic gradients in the context of training GFlowNets. Then, we verify that properly minimizing these divergences yields a provably correct and empirically effective training scheme, often leading to significantly faster convergence than previously proposed optimization. To achieve this, we design control variates based on the REINFORCE leave-one-out and score-matching estimators to reduce the variance of the learning objectives' gradients. Our work contributes by narrowing the gap between GFlowNets training and generalized variational approximations, paving the way for algorithmic ideas informed by the divergence minimization viewpoint.

Embarrassingly Parallel GFlowNets

GFlowNets are a promising alternative to MCMC sampling for discrete compositional random variables. Training GFlowNets requires repeated evaluations of the unnormalized target distribution or reward function. However, for large-scale posterior sampling, this may be prohibitive since it incurs traversing the data several times. Moreover, if the data are distributed across clients, employing standard GFlowNets leads to intensive client-server communication. To alleviate both these issues, we propose embarrassingly parallel GFlowNet (EP-GFlowNet). EP-GFlowNet is a provably correct divide-and-conquer method to sample from product distributions of the form $R(\cdot) \propto R_1(\cdot) ... R_N(\cdot)$ -- e.g., in parallel or federated Bayes, where each $R_n$ is a local posterior defined on a data partition. First, in parallel, we train a local GFlowNet targeting each $R_n$ and send the resulting models to the server. Then, the server learns a global GFlowNet by enforcing our newly proposed \emph{aggregating balance} condition, requiring a single communication step. Importantly, EP-GFlowNets can also be applied to multi-objective optimization and model reuse. Our experiments illustrate the EP-GFlowNets's effectiveness on many tasks, including parallel Bayesian phylogenetics, multi-objective multiset, sequence generation, and federated Bayesian structure learning.

In-n-Out: Calibrating Graph Neural Networks for Link Prediction

Deep neural networks are notoriously miscalibrated, i.e., their outputs do not reflect the true probability of the event we aim to predict. While networks for tabular or image data are usually overconfident, recent works have shown that graph neural networks (GNNs) show the opposite behavior for node-level classification. But what happens when we are predicting links? We show that, in this case, GNNs often exhibit a mixed behavior. More specifically, they may be overconfident in negative predictions while being underconfident in positive ones. Based on this observation, we propose IN-N-OUT, the first-ever method to calibrate GNNs for link prediction. IN-N-OUT is based on two simple intuitions: i) attributing true/false labels to an edge while respecting a GNNs prediction should cause but small fluctuations in that edge's embedding; and, conversely, ii) if we label that same edge contradicting our GNN, embeddings should change more substantially. An extensive experimental campaign shows that IN-N-OUT significantly improves the calibration of GNNs in link prediction, consistently outperforming the baselines available -- which are not designed for this specific task.

Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.

Human-in-the-Loop Causal Discovery under Latent Confounding using Ancestral GFlowNets

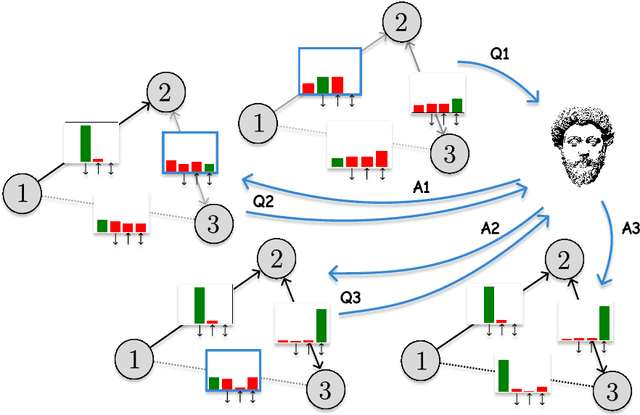
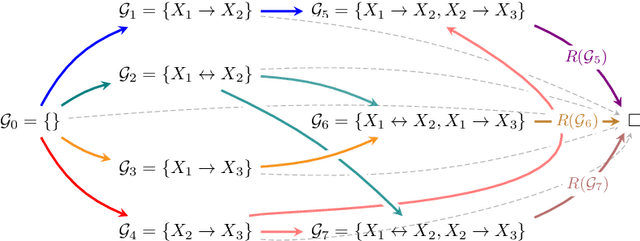
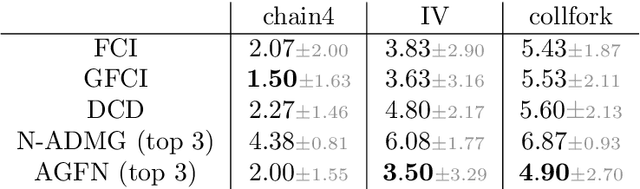
Structure learning is the crux of causal inference. Notably, causal discovery (CD) algorithms are brittle when data is scarce, possibly inferring imprecise causal relations that contradict expert knowledge -- especially when considering latent confounders. To aggravate the issue, most CD methods do not provide uncertainty estimates, making it hard for users to interpret results and improve the inference process. Surprisingly, while CD is a human-centered affair, no works have focused on building methods that both 1) output uncertainty estimates that can be verified by experts and 2) interact with those experts to iteratively refine CD. To solve these issues, we start by proposing to sample (causal) ancestral graphs proportionally to a belief distribution based on a score function, such as the Bayesian information criterion (BIC), using generative flow networks. Then, we leverage the diversity in candidate graphs and introduce an optimal experimental design to iteratively probe the expert about the relations among variables, effectively reducing the uncertainty of our belief over ancestral graphs. Finally, we update our samples to incorporate human feedback via importance sampling. Importantly, our method does not require causal sufficiency (i.e., unobserved confounders may exist). Experiments with synthetic observational data show that our method can accurately sample from distributions over ancestral graphs and that we can greatly improve inference quality with human aid.

Locking and Quacking: Stacking Bayesian model predictions by log-pooling and superposition

Combining predictions from different models is a central problem in Bayesian inference and machine learning more broadly. Currently, these predictive distributions are almost exclusively combined using linear mixtures such as Bayesian model averaging, Bayesian stacking, and mixture of experts. Such linear mixtures impose idiosyncrasies that might be undesirable for some applications, such as multi-modality. While there exist alternative strategies (e.g. geometric bridge or superposition), optimising their parameters usually involves computing an intractable normalising constant repeatedly. We present two novel Bayesian model combination tools. These are generalisations of model stacking, but combine posterior densities by log-linear pooling (locking) and quantum superposition (quacking). To optimise model weights while avoiding the burden of normalising constants, we investigate the Hyvarinen score of the combined posterior predictions. We demonstrate locking with an illustrative example and discuss its practical application with importance sampling.

Distill n' Explain: explaining graph neural networks using simple surrogates

Explaining node predictions in graph neural networks (GNNs) often boils down to finding graph substructures that preserve predictions. Finding these structures usually implies back-propagating through the GNN, bonding the complexity (e.g., number of layers) of the GNN to the cost of explaining it. This naturally begs the question: Can we break this bond by explaining a simpler surrogate GNN? To answer the question, we propose Distill n' Explain (DnX). First, DnX learns a surrogate GNN via knowledge distillation. Then, DnX extracts node or edge-level explanations by solving a simple convex program. We also propose FastDnX, a faster version of DnX that leverages the linear decomposition of our surrogate model. Experiments show that DnX and FastDnX often outperform state-of-the-art GNN explainers while being orders of magnitude faster. Additionally, we support our empirical findings with theoretical results linking the quality of the surrogate model (i.e., distillation error) to the faithfulness of explanations.

Provably expressive temporal graph networks

Temporal graph networks (TGNs) have gained prominence as models for embedding dynamic interactions, but little is known about their theoretical underpinnings. We establish fundamental results about the representational power and limits of the two main categories of TGNs: those that aggregate temporal walks (WA-TGNs), and those that augment local message passing with recurrent memory modules (MP-TGNs). Specifically, novel constructions reveal the inadequacy of MP-TGNs and WA-TGNs, proving that neither category subsumes the other. We extend the 1-WL (Weisfeiler-Leman) test to temporal graphs, and show that the most powerful MP-TGNs should use injective updates, as in this case they become as expressive as the temporal WL. Also, we show that sufficiently deep MP-TGNs cannot benefit from memory, and MP/WA-TGNs fail to compute graph properties such as girth. These theoretical insights lead us to PINT -- a novel architecture that leverages injective temporal message passing and relative positional features. Importantly, PINT is provably more expressive than both MP-TGNs and WA-TGNs. PINT significantly outperforms existing TGNs on several real-world benchmarks.

Parallel MCMC Without Embarrassing Failures

Embarrassingly parallel Markov Chain Monte Carlo (MCMC) exploits parallel computing to scale Bayesian inference to large datasets by using a two-step approach. First, MCMC is run in parallel on (sub)posteriors defined on data partitions. Then, a server combines local results. While efficient, this framework is very sensitive to the quality of subposterior sampling. Common sampling problems such as missing modes or misrepresentation of low-density regions are amplified -- instead of being corrected -- in the combination phase, leading to catastrophic failures. In this work, we propose a novel combination strategy to mitigate this issue. Our strategy, Parallel Active Inference (PAI), leverages Gaussian Process (GP) surrogate modeling and active learning. After fitting GPs to subposteriors, PAI (i) shares information between GP surrogates to cover missing modes; and (ii) uses active sampling to individually refine subposterior approximations. We validate PAI in challenging benchmarks, including heavy-tailed and multi-modal posteriors and a real-world application to computational neuroscience. Empirical results show that PAI succeeds where previous methods catastrophically fail, with a small communication overhead.