Predictive variational inference: Learn the predictively optimal posterior distribution

Vanilla variational inference finds an optimal approximation to the Bayesian posterior distribution, but even the exact Bayesian posterior is often not meaningful under model misspecification. We propose predictive variational inference (PVI): a general inference framework that seeks and samples from an optimal posterior density such that the resulting posterior predictive distribution is as close to the true data generating process as possible, while this this closeness is measured by multiple scoring rules. By optimizing the objective, the predictive variational inference is generally not the same as, or even attempting to approximate, the Bayesian posterior, even asymptotically. Rather, we interpret it as implicit hierarchical expansion. Further, the learned posterior uncertainty detects heterogeneity of parameters among the population, enabling automatic model diagnosis. This framework applies to both likelihood-exact and likelihood-free models. We demonstrate its application in real data examples.

Simulation based stacking

Simulation-based inference has been popular for amortized Bayesian computation. It is typical to have more than one posterior approximation, from different inference algorithms, different architectures, or simply the randomness of initialization and stochastic gradients. With a provable asymptotic guarantee, we present a general stacking framework to make use of all available posterior approximations. Our stacking method is able to combine densities, simulation draws, confidence intervals, and moments, and address the overall precision, calibration, coverage, and bias at the same time. We illustrate our method on several benchmark simulations and a challenging cosmological inference task.

Variational Inference with Gaussian Score Matching

Variational inference (VI) is a method to approximate the computationally intractable posterior distributions that arise in Bayesian statistics. Typically, VI fits a simple parametric distribution to the target posterior by minimizing an appropriate objective such as the evidence lower bound (ELBO). In this work, we present a new approach to VI based on the principle of score matching, that if two distributions are equal then their score functions (i.e., gradients of the log density) are equal at every point on their support. With this, we develop score matching VI, an iterative algorithm that seeks to match the scores between the variational approximation and the exact posterior. At each iteration, score matching VI solves an inner optimization, one that minimally adjusts the current variational estimate to match the scores at a newly sampled value of the latent variables. We show that when the variational family is a Gaussian, this inner optimization enjoys a closed form solution, which we call Gaussian score matching VI (GSM-VI). GSM-VI is also a ``black box'' variational algorithm in that it only requires a differentiable joint distribution, and as such it can be applied to a wide class of models. We compare GSM-VI to black box variational inference (BBVI), which has similar requirements but instead optimizes the ELBO. We study how GSM-VI behaves as a function of the problem dimensionality, the condition number of the target covariance matrix (when the target is Gaussian), and the degree of mismatch between the approximating and exact posterior distribution. We also study GSM-VI on a collection of real-world Bayesian inference problems from the posteriorDB database of datasets and models. In all of our studies we find that GSM-VI is faster than BBVI, but without sacrificing accuracy. It requires 10-100x fewer gradient evaluations to obtain a comparable quality of approximation.

Discriminative calibration

To check the accuracy of Bayesian computations, it is common to use rank-based simulation-based calibration (SBC). However, SBC has drawbacks: The test statistic is somewhat ad-hoc, interactions are difficult to examine, multiple testing is a challenge, and the resulting p-value is not a divergence metric. We propose to replace the marginal rank test with a flexible classification approach that learns test statistics from data. This measure typically has a higher statistical power than the SBC rank test and returns an interpretable divergence measure of miscalibration, computed from classification accuracy. This approach can be used with different data generating processes to address likelihood-free inference or traditional inference methods like Markov chain Monte Carlo or variational inference. We illustrate an automated implementation using neural networks and statistically-inspired features, and validate the method with numerical and real data experiments.

Locking and Quacking: Stacking Bayesian model predictions by log-pooling and superposition

Combining predictions from different models is a central problem in Bayesian inference and machine learning more broadly. Currently, these predictive distributions are almost exclusively combined using linear mixtures such as Bayesian model averaging, Bayesian stacking, and mixture of experts. Such linear mixtures impose idiosyncrasies that might be undesirable for some applications, such as multi-modality. While there exist alternative strategies (e.g. geometric bridge or superposition), optimising their parameters usually involves computing an intractable normalising constant repeatedly. We present two novel Bayesian model combination tools. These are generalisations of model stacking, but combine posterior densities by log-linear pooling (locking) and quantum superposition (quacking). To optimise model weights while avoiding the burden of normalising constants, we investigate the Hyvarinen score of the combined posterior predictions. We demonstrate locking with an illustrative example and discuss its practical application with importance sampling.

Bayesian hierarchical stacking

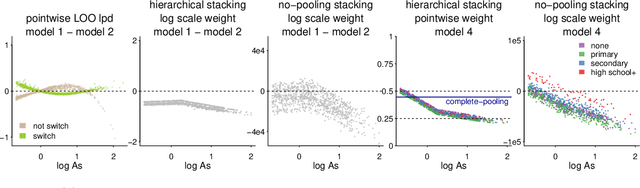
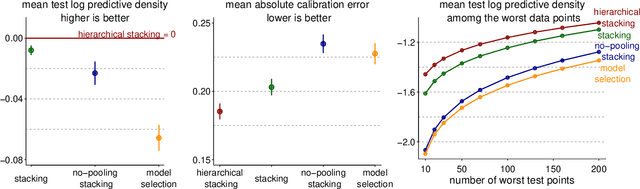
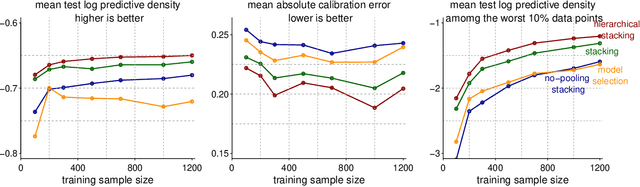
Stacking is a widely used model averaging technique that yields asymptotically optimal prediction among all linear averages. We show that stacking is most effective when the model predictive performance is heterogeneous in inputs, so that we can further improve the stacked mixture with a hierarchical model. With the input-varying yet partially-pooled model weights, hierarchical stacking improves average and conditional predictions. Our Bayesian formulation includes constant-weight (complete-pooling) stacking as a special case. We generalize to incorporate discrete and continuous inputs, other structured priors, and time-series and longitudinal data. We demonstrate on several applied problems.

Stacking for Non-mixing Bayesian Computations: The Curse and Blessing of Multimodal Posteriors

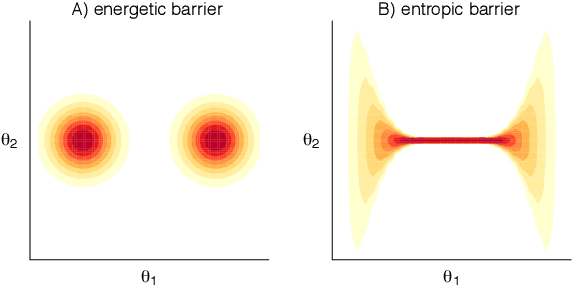
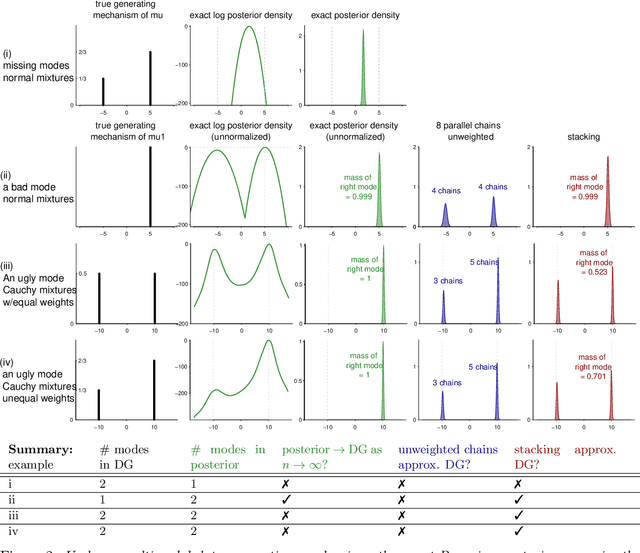
When working with multimodal Bayesian posterior distributions, Markov chain Monte Carlo (MCMC) algorithms can have difficulty moving between modes, and default variational or mode-based approximate inferences will understate posterior uncertainty. And, even if the most important modes can be found, it is difficult to evaluate their relative weights in the posterior. Here we propose an alternative approach, using parallel runs of MCMC, variational, or mode-based inference to hit as many modes or separated regions as possible, and then combining these using importance sampling based Bayesian stacking, a scalable method for constructing a weighted average of distributions so as to maximize cross-validated prediction utility. The result from stacking is not necessarily equivalent, even asymptotically, to fully Bayesian inference, but it serves many of the same goals. Under misspecified models, stacking can give better predictive performance than full Bayesian inference, hence the multimodality can be considered a blessing rather than a curse. We explore with an example where the stacked inference approximates the true data generating process from the misspecified model, an example of inconsistent inference, and non-mixing samplers. We elaborate the practical implantation in the context of latent Dirichlet allocation, Gaussian process regression, hierarchical model, variational inference in horseshoe regression, and neural networks.

Ensemble Model Patching: A Parameter-Efficient Variational Bayesian Neural Network

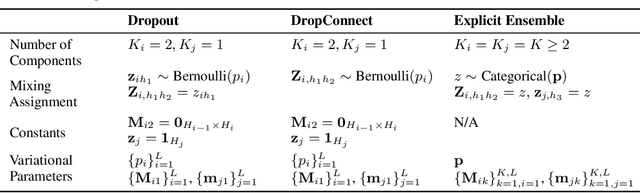
Two main obstacles preventing the widespread adoption of variational Bayesian neural networks are the high parameter overhead that makes them infeasible on large networks, and the difficulty of implementation, which can be thought of as "programming overhead." MC dropout [Gal and Ghahramani, 2016] is popular because it sidesteps these obstacles. Nevertheless, dropout is often harmful to model performance when used in networks with batch normalization layers [Li et al., 2018], which are an indispensable part of modern neural networks. We construct a general variational family for ensemble-based Bayesian neural networks that encompasses dropout as a special case. We further present two specific members of this family that work well with batch normalization layers, while retaining the benefits of low parameter and programming overhead, comparable to non-Bayesian training. Our proposed methods improve predictive accuracy and achieve almost perfect calibration on a ResNet-18 trained with ImageNet.

Yes, but Did It Work?: Evaluating Variational Inference

While it's always possible to compute a variational approximation to a posterior distribution, it can be difficult to discover problems with this approximation. We propose two diagnostic algorithms to alleviate this problem. The Pareto-smoothed importance sampling (PSIS) diagnostic gives a goodness of fit measurement for joint distributions, while simultaneously improving the error in the estimate. The variational simulation-based calibration (VSBC) assesses the average performance of point estimates.