Quasi-random Multi-Sample Inference for Large Language Models

Large language models (LLMs) are often equipped with multi-sample decoding strategies. An LLM implicitly defines an arithmetic code book, facilitating efficient and embarrassingly parallelizable \textbf{arithmetic sampling} to produce multiple samples using quasi-random codes. Traditional text generation methods, such as beam search and sampling-based techniques, have notable limitations: they lack parallelizability or diversity of sampled sequences. This study explores the potential of arithmetic sampling, contrasting it with ancestral sampling across two decoding tasks that employ multi-sample inference: chain-of-thought reasoning with self-consistency and machine translation with minimum Bayes risk decoding. Our results demonstrate that arithmetic sampling produces more diverse samples, significantly improving reasoning and translation performance as the sample size increases. We observe a $\mathbf{3\text{-}5\%}$ point increase in accuracy on the GSM8K dataset and a $\mathbf{0.45\text{-}0.89\%}$ point increment in COMET score for WMT19 tasks using arithmetic sampling without any significant computational overhead.

Hamiltonian Monte Carlo Inference of Marginalized Linear Mixed-Effects Models

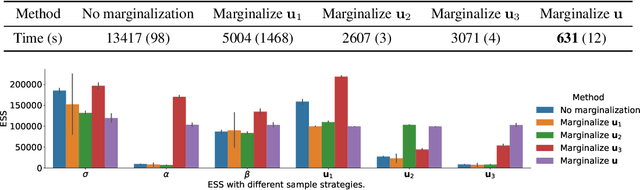
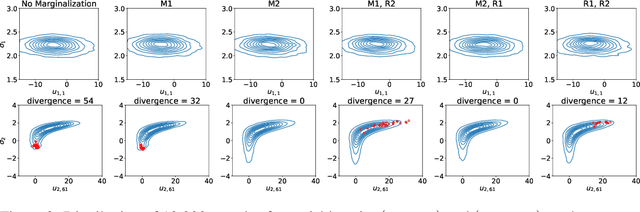
Bayesian reasoning in linear mixed-effects models (LMMs) is challenging and often requires advanced sampling techniques like Markov chain Monte Carlo (MCMC). A common approach is to write the model in a probabilistic programming language and then sample via Hamiltonian Monte Carlo (HMC). However, there are many ways a user can transform a model that make inference more or less efficient. In particular, marginalizing some variables can greatly improve inference but is difficult for users to do manually. We develop an algorithm to easily marginalize random effects in LMMs. A naive approach introduces cubic time operations within an inference algorithm like HMC, but we reduce the running time to linear using fast linear algebra techniques. We show that marginalization is always beneficial when applicable and highlight improvements in various models, especially ones from cognitive sciences.

Predictive variational inference: Learn the predictively optimal posterior distribution

Vanilla variational inference finds an optimal approximation to the Bayesian posterior distribution, but even the exact Bayesian posterior is often not meaningful under model misspecification. We propose predictive variational inference (PVI): a general inference framework that seeks and samples from an optimal posterior density such that the resulting posterior predictive distribution is as close to the true data generating process as possible, while this this closeness is measured by multiple scoring rules. By optimizing the objective, the predictive variational inference is generally not the same as, or even attempting to approximate, the Bayesian posterior, even asymptotically. Rather, we interpret it as implicit hierarchical expansion. Further, the learned posterior uncertainty detects heterogeneity of parameters among the population, enabling automatic model diagnosis. This framework applies to both likelihood-exact and likelihood-free models. We demonstrate its application in real data examples.

Automatically Marginalized MCMC in Probabilistic Programming

Hamiltonian Monte Carlo (HMC) is a powerful algorithm to sample latent variables from Bayesian models. The advent of probabilistic programming languages (PPLs) frees users from writing inference algorithms and lets users focus on modeling. However, many models are difficult for HMC to solve directly, which often require tricks like model reparameterization. We are motivated by the fact that many of those models could be simplified by marginalization. We propose to use automatic marginalization as part of the sampling process using HMC in a graphical model extracted from a PPL, which substantially improves sampling from real-world hierarchical models.

Variational Marginal Particle Filters

Variational inference for state space models (SSMs) is known to be hard in general. Recent works focus on deriving variational objectives for SSMs from unbiased sequential Monte Carlo estimators. We reveal that the marginal particle filter is obtained from sequential Monte Carlo by applying Rao-Blackwellization operations, which sacrifices the trajectory information for reduced variance and differentiability. We propose the variational marginal particle filter (VMPF), which is a differentiable and reparameterizable variational filtering objective for SSMs based on an unbiased estimator. We find that VMPF with biased gradients gives tighter bounds than previous objectives, and the unbiased reparameterization gradients are sometimes beneficial.

Optimal Mixture Weights for Off-Policy Evaluation with Multiple Behavior Policies

Off-policy evaluation is a key component of reinforcement learning which evaluates a target policy with offline data collected from behavior policies. It is a crucial step towards safe reinforcement learning and has been used in advertisement, recommender systems and many other applications. In these applications, sometimes the offline data is collected from multiple behavior policies. Previous works regard data from different behavior policies equally. Nevertheless, some behavior policies are better at producing good estimators while others are not. This paper starts with discussing how to correctly mix estimators produced by different behavior policies. We propose three ways to reduce the variance of the mixture estimator when all sub-estimators are unbiased or asymptotically unbiased. Furthermore, experiments on simulated recommender systems show that our methods are effective in reducing the Mean-Square Error of estimation.

On the Necessity and Effectiveness of Learning the Prior of Variational Auto-Encoder

Using powerful posterior distributions is a popular approach to achieving better variational inference. However, recent works showed that the aggregated posterior may fail to match unit Gaussian prior, thus learning the prior becomes an alternative way to improve the lower-bound. In this paper, for the first time in the literature, we prove the necessity and effectiveness of learning the prior when aggregated posterior does not match unit Gaussian prior, analyze why this situation may happen, and propose a hypothesis that learning the prior may improve reconstruction loss, all of which are supported by our extensive experiment results. We show that using learned Real NVP prior and just one latent variable in VAE, we can achieve test NLL comparable to very deep state-of-the-art hierarchical VAE, outperforming many previous works with complex hierarchical VAE architectures.