Hamiltonian Monte Carlo Inference of Marginalized Linear Mixed-Effects Models

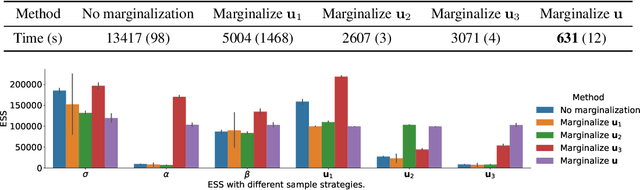
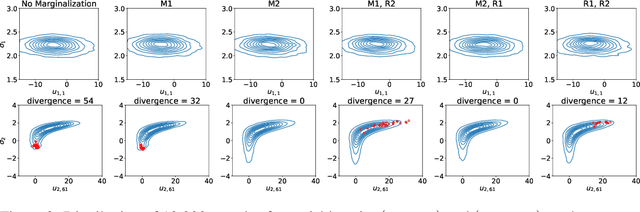
Bayesian reasoning in linear mixed-effects models (LMMs) is challenging and often requires advanced sampling techniques like Markov chain Monte Carlo (MCMC). A common approach is to write the model in a probabilistic programming language and then sample via Hamiltonian Monte Carlo (HMC). However, there are many ways a user can transform a model that make inference more or less efficient. In particular, marginalizing some variables can greatly improve inference but is difficult for users to do manually. We develop an algorithm to easily marginalize random effects in LMMs. A naive approach introduces cubic time operations within an inference algorithm like HMC, but we reduce the running time to linear using fast linear algebra techniques. We show that marginalization is always beneficial when applicable and highlight improvements in various models, especially ones from cognitive sciences.

Efficient and Private Marginal Reconstruction with Local Non-Negativity

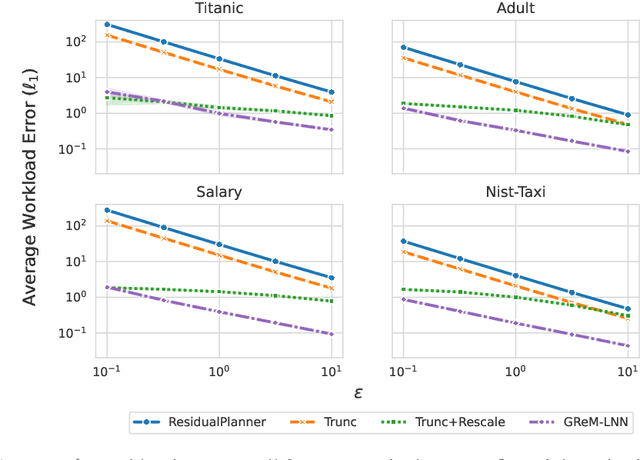
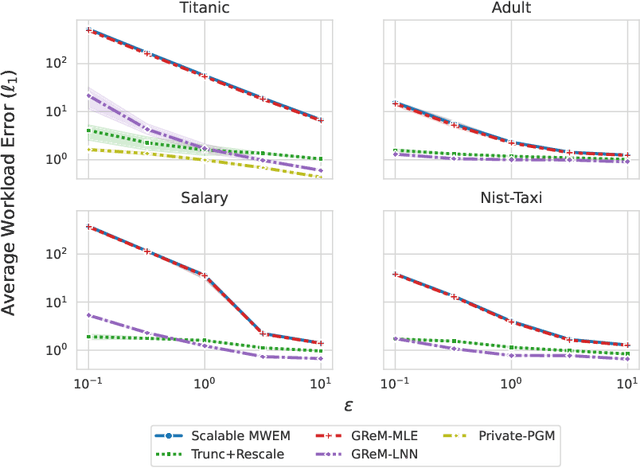
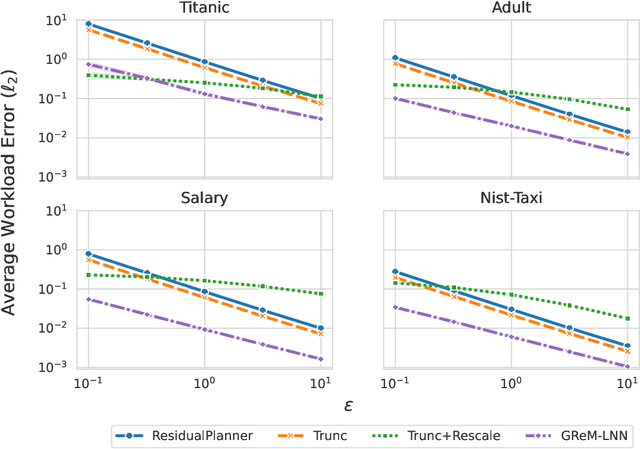
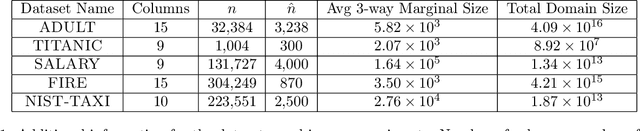
Differential privacy is the dominant standard for formal and quantifiable privacy and has been used in major deployments that impact millions of people. Many differentially private algorithms for query release and synthetic data contain steps that reconstruct answers to queries from answers to other queries measured by the mechanism. Reconstruction is an important subproblem for such mechanisms to economize the privacy budget, minimize error on reconstructed answers, and allow for scalability to high-dimensional datasets. In this paper, we introduce a principled and efficient postprocessing method ReM (Residuals-to-Marginals) for reconstructing answers to marginal queries. Our method builds on recent work on efficient mechanisms for marginal query release, based on making measurements using a residual query basis that admits efficient pseudoinversion, which is an important primitive used in reconstruction. An extension GReM-LNN (Gaussian Residuals-to-Marginals with Local Non-negativity) reconstructs marginals under Gaussian noise satisfying consistency and non-negativity, which often reduces error on reconstructed answers. We demonstrate the utility of ReM and GReM-LNN by applying them to improve existing private query answering mechanisms: ResidualPlanner and MWEM.

Private Regression via Data-Dependent Sufficient Statistic Perturbation

Sufficient statistic perturbation (SSP) is a widely used method for differentially private linear regression. SSP adopts a data-independent approach where privacy noise from a simple distribution is added to sufficient statistics. However, sufficient statistics can often be expressed as linear queries and better approximated by data-dependent mechanisms. In this paper we introduce data-dependent SSP for linear regression based on post-processing privately released marginals, and find that it outperforms state-of-the-art data-independent SSP. We extend this result to logistic regression by developing an approximate objective that can be expressed in terms of sufficient statistics, resulting in a novel and highly competitive SSP approach for logistic regression. We also make a connection to synthetic data for machine learning: for models with sufficient statistics, training on synthetic data corresponds to data-dependent SSP, with the overall utility determined by how well the mechanism answers these linear queries.

Joint Selection: Adaptively Incorporating Public Information for Private Synthetic Data

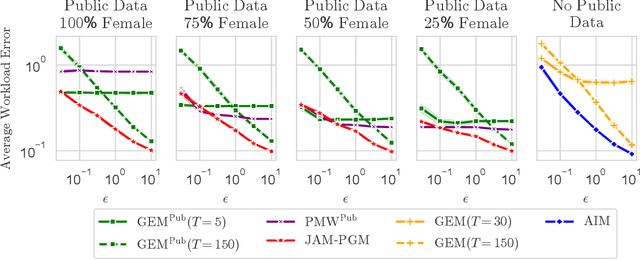
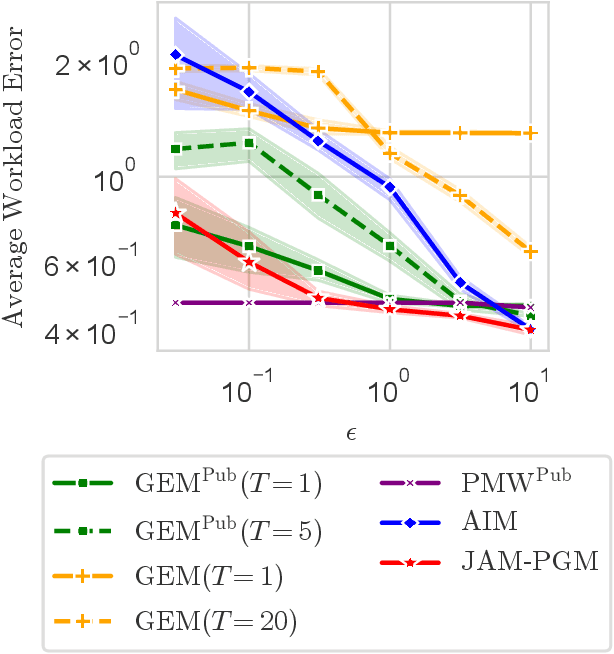
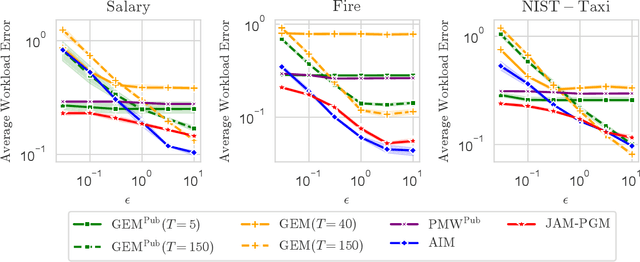
Mechanisms for generating differentially private synthetic data based on marginals and graphical models have been successful in a wide range of settings. However, one limitation of these methods is their inability to incorporate public data. Initializing a data generating model by pre-training on public data has shown to improve the quality of synthetic data, but this technique is not applicable when model structure is not determined a priori. We develop the mechanism jam-pgm, which expands the adaptive measurements framework to jointly select between measuring public data and private data. This technique allows for public data to be included in a graphical-model-based mechanism. We show that jam-pgm is able to outperform both publicly assisted and non publicly assisted synthetic data generation mechanisms even when the public data distribution is biased.

Human in-the-Loop Estimation of Cluster Count in Datasets via Similarity-Driven Nested Importance Sampling

Identifying the number of clusters serves as a preliminary goal for many data analysis tasks. A common approach to this problem is to vary the number of clusters in a clustering algorithm (e.g., 'k' in $k$-means) and pick the value that best explains the data. However, the count estimates can be unreliable especially when the image similarity is poor. Human feedback on the pairwise similarity can be used to improve the clustering, but existing approaches do not guarantee accurate count estimates. We propose an approach to produce estimates of the cluster counts in a large dataset given an approximate pairwise similarity. Our framework samples edges guided by the pairwise similarity, and we collect human feedback to construct a statistical estimate of the cluster count. On the technical front we have developed a nested importance sampling approach that yields (asymptotically) unbiased estimates of the cluster count with confidence intervals which can guide human effort. Compared to naive sampling, our similarity-driven sampling produces more accurate estimates of counts and tighter confidence intervals. We evaluate our method on a benchmark of six fine-grained image classification datasets achieving low error rates on the estimated number of clusters with significantly less human labeling effort compared to baselines and alternative active clustering approaches.

DISCount: Counting in Large Image Collections with Detector-Based Importance Sampling

Many modern applications use computer vision to detect and count objects in massive image collections. However, when the detection task is very difficult or in the presence of domain shifts, the counts may be inaccurate even with significant investments in training data and model development. We propose DISCount -- a detector-based importance sampling framework for counting in large image collections that integrates an imperfect detector with human-in-the-loop screening to produce unbiased estimates of counts. We propose techniques for solving counting problems over multiple spatial or temporal regions using a small number of screened samples and estimate confidence intervals. This enables end-users to stop screening when estimates are sufficiently accurate, which is often the goal in a scientific study. On the technical side we develop variance reduction techniques based on control variates and prove the (conditional) unbiasedness of the estimators. DISCount leads to a 9-12x reduction in the labeling costs over naive screening for tasks we consider, such as counting birds in radar imagery or estimating damaged buildings in satellite imagery, and also surpasses alternative covariate-based screening approaches in efficiency.

Kernel Interpolation with Sparse Grids

Structured kernel interpolation (SKI) accelerates Gaussian process (GP) inference by interpolating the kernel covariance function using a dense grid of inducing points, whose corresponding kernel matrix is highly structured and thus amenable to fast linear algebra. Unfortunately, SKI scales poorly in the dimension of the input points, since the dense grid size grows exponentially with the dimension. To mitigate this issue, we propose the use of sparse grids within the SKI framework. These grids enable accurate interpolation, but with a number of points growing more slowly with dimension. We contribute a novel nearly linear time matrix-vector multiplication algorithm for the sparse grid kernel matrix. Next, we describe how sparse grids can be combined with an efficient interpolation scheme based on simplices. With these changes, we demonstrate that SKI can be scaled to higher dimensions while maintaining accuracy.

Sample Average Approximation for Black-Box VI

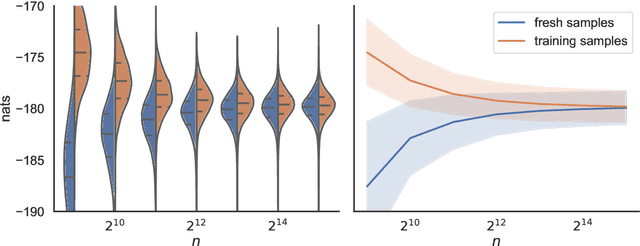
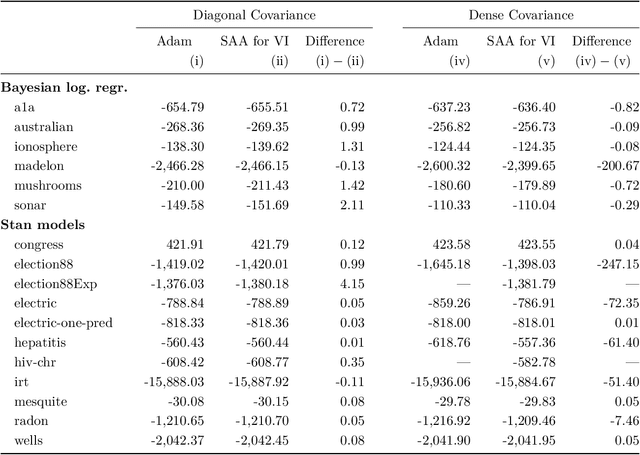
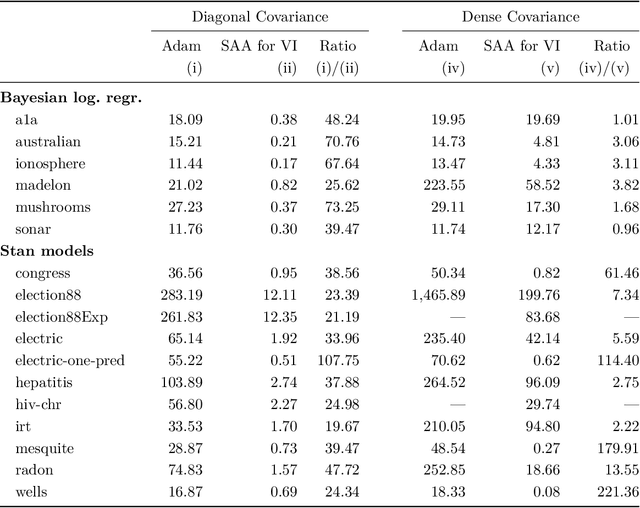
We present a novel approach for black-box VI that bypasses the difficulties of stochastic gradient ascent, including the task of selecting step-sizes. Our approach involves using a sequence of sample average approximation (SAA) problems. SAA approximates the solution of stochastic optimization problems by transforming them into deterministic ones. We use quasi-Newton methods and line search to solve each deterministic optimization problem and present a heuristic policy to automate hyperparameter selection. Our experiments show that our method simplifies the VI problem and achieves faster performance than existing methods.

U-Statistics for Importance-Weighted Variational Inference

We propose the use of U-statistics to reduce variance for gradient estimation in importance-weighted variational inference. The key observation is that, given a base gradient estimator that requires $m > 1$ samples and a total of $n > m$ samples to be used for estimation, lower variance is achieved by averaging the base estimator on overlapping batches of size $m$ than disjoint batches, as currently done. We use classical U-statistic theory to analyze the variance reduction, and propose novel approximations with theoretical guarantees to ensure computational efficiency. We find empirically that U-statistic variance reduction can lead to modest to significant improvements in inference performance on a range of models, with little computational cost.

Automatically Marginalized MCMC in Probabilistic Programming

Hamiltonian Monte Carlo (HMC) is a powerful algorithm to sample latent variables from Bayesian models. The advent of probabilistic programming languages (PPLs) frees users from writing inference algorithms and lets users focus on modeling. However, many models are difficult for HMC to solve directly, which often require tricks like model reparameterization. We are motivated by the fact that many of those models could be simplified by marginalization. We propose to use automatic marginalization as part of the sampling process using HMC in a graphical model extracted from a PPL, which substantially improves sampling from real-world hierarchical models.