U-Statistics for Importance-Weighted Variational Inference

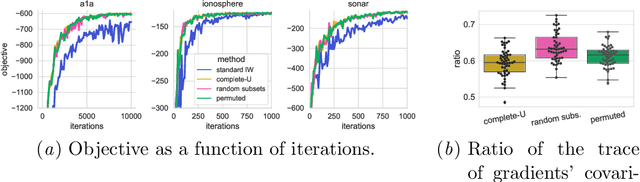
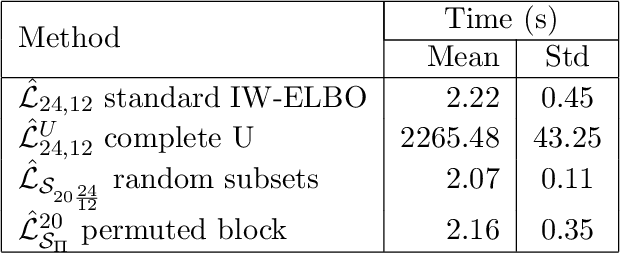
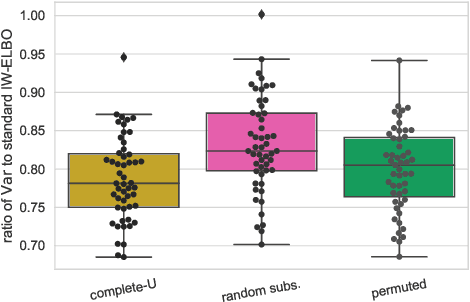
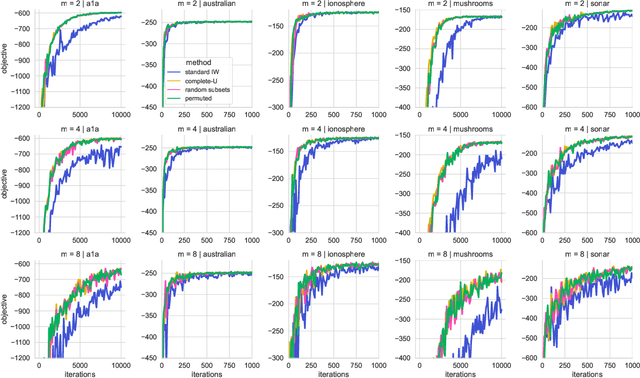
We propose the use of U-statistics to reduce variance for gradient estimation in importance-weighted variational inference. The key observation is that, given a base gradient estimator that requires $m > 1$ samples and a total of $n > m$ samples to be used for estimation, lower variance is achieved by averaging the base estimator on overlapping batches of size $m$ than disjoint batches, as currently done. We use classical U-statistic theory to analyze the variance reduction, and propose novel approximations with theoretical guarantees to ensure computational efficiency. We find empirically that U-statistic variance reduction can lead to modest to significant improvements in inference performance on a range of models, with little computational cost.

Causal Inference using Gaussian Processes with Structured Latent Confounders

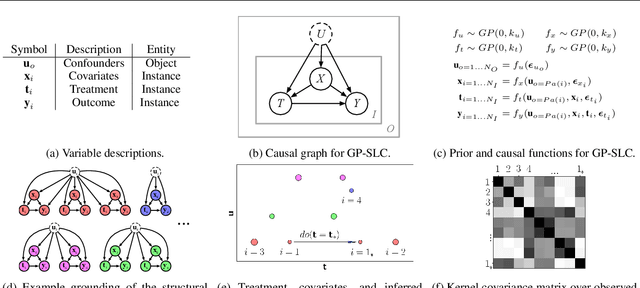
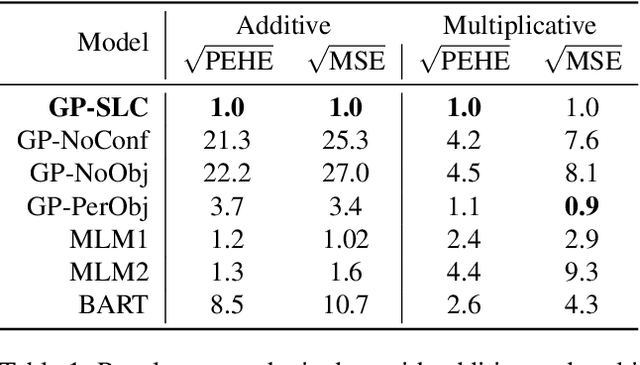
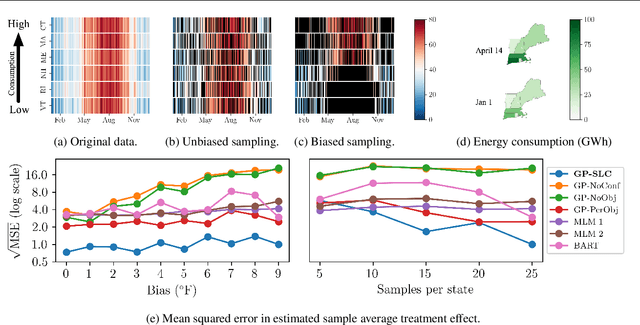
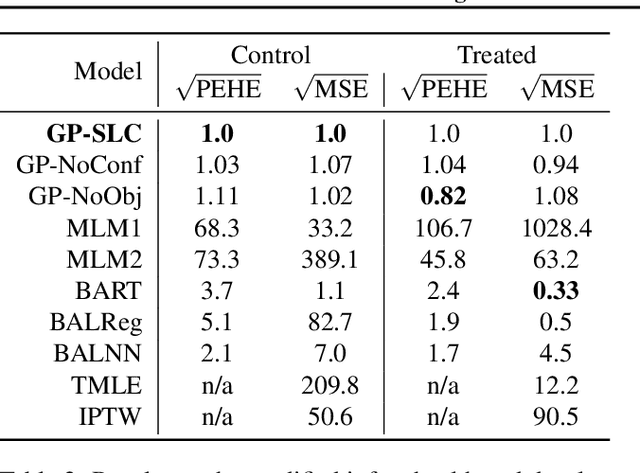
Latent confounders---unobserved variables that influence both treatment and outcome---can bias estimates of causal effects. In some cases, these confounders are shared across observations, e.g. all students taking a course are influenced by the course's difficulty in addition to any educational interventions they receive individually. This paper shows how to semiparametrically model latent confounders that have this structure and thereby improve estimates of causal effects. The key innovations are a hierarchical Bayesian model, Gaussian processes with structured latent confounders (GP-SLC), and a Monte Carlo inference algorithm for this model based on elliptical slice sampling. GP-SLC provides principled Bayesian uncertainty estimates of individual treatment effect with minimal assumptions about the functional forms relating confounders, covariates, treatment, and outcome. Finally, this paper shows GP-SLC is competitive with or more accurate than widely used causal inference techniques on three benchmark datasets, including the Infant Health and Development Program and a dataset showing the effect of changing temperatures on state-wide energy consumption across New England.

Supervised learning algorithms resilient to discriminatory data perturbations

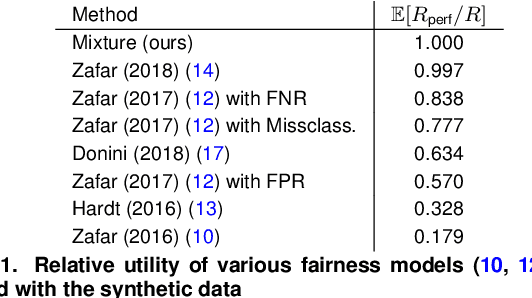
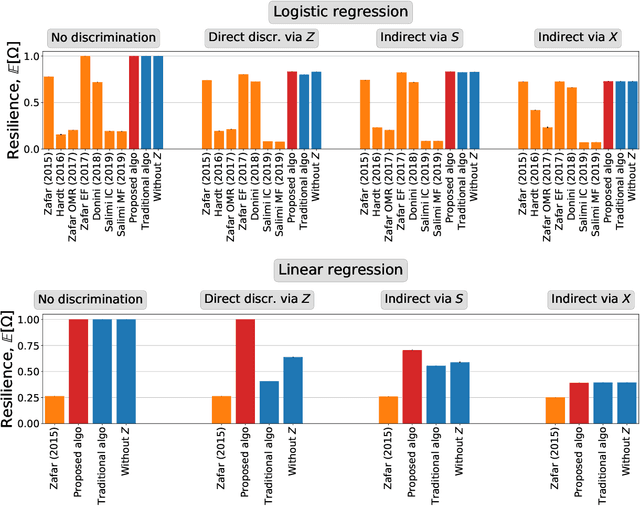
The actions of individuals can be discriminatory with respect to certain protected attributes, such as race or sex. Recently, discrimination has become a focal concern in supervised learning algorithms augmenting human decision-making. These systems are trained using historical data, which may have been tainted by discrimination, and may learn biases against the protected groups. An important question is how to train models without propagating discrimination. Such discrimination can be either direct, when one or more of protected attributes are used in the decision-making directly, or indirect, when other attributes correlated with the protected attributes are used in an unjustified manner. In this work, we i) model discrimination as a perturbation of data-generating process; ii) introduce a measure of resilience of a supervised learning algorithm to potentially discriminatory data perturbations; and iii) propose a novel supervised learning method that is more resilient to such discriminatory perturbations than state-of-the-art learning algorithms addressing discrimination. The proposed method can be used with general supervised learning algorithms, prevents direct discrimination and avoids inducement of indirect discrimination, while maximizing model accuracy.