Model Informed Flows for Bayesian Inference of Probabilistic Programs

Variational inference often struggles with the posterior geometry exhibited by complex hierarchical Bayesian models. Recent advances in flow-based variational families and Variationally Inferred Parameters (VIP) each address aspects of this challenge, but their formal relationship is unexplored. Here, we prove that the combination of VIP and a full-rank Gaussian can be represented exactly as a forward autoregressive flow augmented with a translation term and input from the model's prior. Guided by this theoretical insight, we introduce the Model-Informed Flow (MIF) architecture, which adds the necessary translation mechanism, prior information, and hierarchical ordering. Empirically, MIF delivers tighter posterior approximations and matches or exceeds state-of-the-art performance across a suite of hierarchical and non-hierarchical benchmarks.

Large Language Bayes

Many domain experts do not have the time or training to write formal Bayesian models. This paper takes an informal problem description as input, and combines a large language model and a probabilistic programming language to create a joint distribution over formal models, latent variables, and data. A posterior over latent variables follows by conditioning on observed data and integrating over formal models. This presents a challenging inference problem. We suggest an inference recipe that amounts to generating many formal models from the large language model, performing approximate inference on each, and then doing a weighted average. This is justified an analyzed as a combination of self-normalized importance sampling, MCMC, and variational inference. We show that this produces sensible predictions without the need to specify a formal model.

Disentangling impact of capacity, objective, batchsize, estimators, and step-size on flow VI

Normalizing flow-based variational inference (flow VI) is a promising approximate inference approach, but its performance remains inconsistent across studies. Numerous algorithmic choices influence flow VI's performance. We conduct a step-by-step analysis to disentangle the impact of some of the key factors: capacity, objectives, gradient estimators, number of gradient estimates (batchsize), and step-sizes. Each step examines one factor while neutralizing others using insights from the previous steps and/or using extensive parallel computation. To facilitate high-fidelity evaluation, we curate a benchmark of synthetic targets that represent common posterior pathologies and allow for exact sampling. We provide specific recommendations for different factors and propose a flow VI recipe that matches or surpasses leading turnkey Hamiltonian Monte Carlo (HMC) methods.

Hamiltonian Monte Carlo Inference of Marginalized Linear Mixed-Effects Models

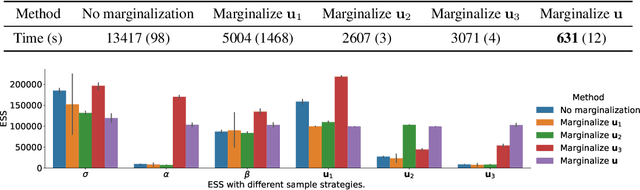
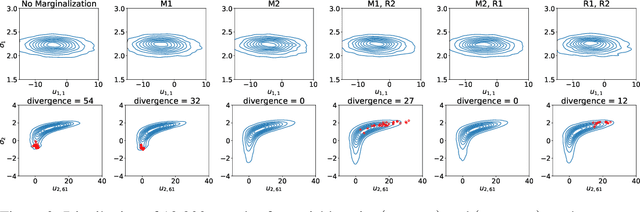
Bayesian reasoning in linear mixed-effects models (LMMs) is challenging and often requires advanced sampling techniques like Markov chain Monte Carlo (MCMC). A common approach is to write the model in a probabilistic programming language and then sample via Hamiltonian Monte Carlo (HMC). However, there are many ways a user can transform a model that make inference more or less efficient. In particular, marginalizing some variables can greatly improve inference but is difficult for users to do manually. We develop an algorithm to easily marginalize random effects in LMMs. A naive approach introduces cubic time operations within an inference algorithm like HMC, but we reduce the running time to linear using fast linear algebra techniques. We show that marginalization is always beneficial when applicable and highlight improvements in various models, especially ones from cognitive sciences.

Understanding and mitigating difficulties in posterior predictive evaluation

Predictive posterior densities (PPDs) are of interest in approximate Bayesian inference. Typically, these are estimated by simple Monte Carlo (MC) averages using samples from the approximate posterior. We observe that the signal-to-noise ratio (SNR) of such estimators can be extremely low. An analysis for exact inference reveals SNR decays exponentially as there is an increase in (a) the mismatch between training and test data, (b) the dimensionality of the latent space, or (c) the size of the test data relative to the training data. Further analysis extends these results to approximate inference. To remedy the low SNR problem, we propose replacing simple MC sampling with importance sampling using a proposal distribution optimized at test time on a variational proxy for the SNR and demonstrate that this yields greatly improved estimates.

Simulation based stacking

Simulation-based inference has been popular for amortized Bayesian computation. It is typical to have more than one posterior approximation, from different inference algorithms, different architectures, or simply the randomness of initialization and stochastic gradients. With a provable asymptotic guarantee, we present a general stacking framework to make use of all available posterior approximations. Our stacking method is able to combine densities, simulation draws, confidence intervals, and moments, and address the overall precision, calibration, coverage, and bias at the same time. We illustrate our method on several benchmark simulations and a challenging cosmological inference task.

Provable convergence guarantees for black-box variational inference

While black-box variational inference is widely used, there is no proof that its stochastic optimization succeeds. We suggest this is due to a theoretical gap in existing stochastic optimization proofs-namely the challenge of gradient estimators with unusual noise bounds, and a composite non-smooth objective. For dense Gaussian variational families, we observe that existing gradient estimators based on reparameterization satisfy a quadratic noise bound and give novel convergence guarantees for proximal and projected stochastic gradient descent using this bound. This provides the first rigorous guarantee that black-box variational inference converges for realistic inference problems.

Discriminative calibration

To check the accuracy of Bayesian computations, it is common to use rank-based simulation-based calibration (SBC). However, SBC has drawbacks: The test statistic is somewhat ad-hoc, interactions are difficult to examine, multiple testing is a challenge, and the resulting p-value is not a divergence metric. We propose to replace the marginal rank test with a flexible classification approach that learns test statistics from data. This measure typically has a higher statistical power than the SBC rank test and returns an interpretable divergence measure of miscalibration, computed from classification accuracy. This approach can be used with different data generating processes to address likelihood-free inference or traditional inference methods like Markov chain Monte Carlo or variational inference. We illustrate an automated implementation using neural networks and statistically-inspired features, and validate the method with numerical and real data experiments.

Sample Average Approximation for Black-Box VI

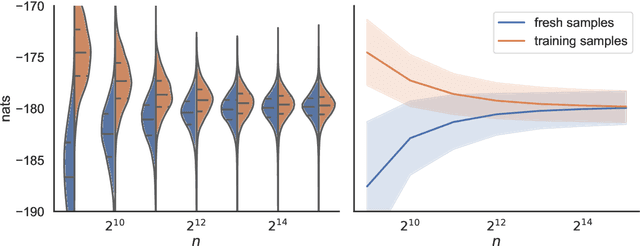
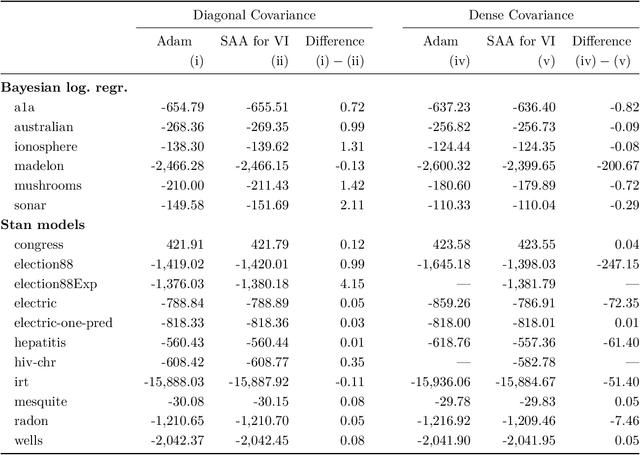
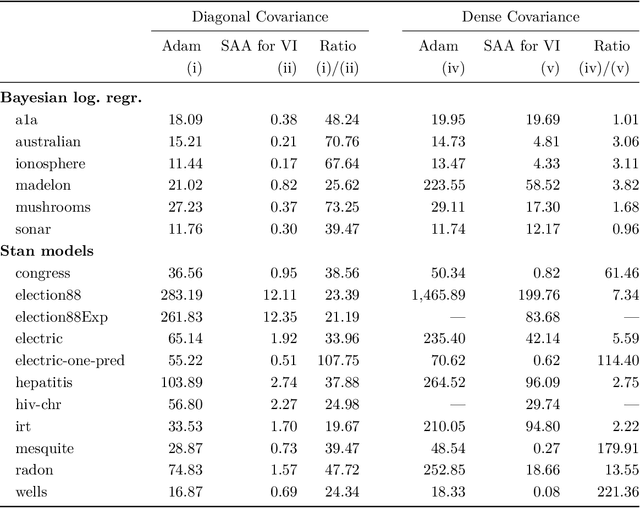
We present a novel approach for black-box VI that bypasses the difficulties of stochastic gradient ascent, including the task of selecting step-sizes. Our approach involves using a sequence of sample average approximation (SAA) problems. SAA approximates the solution of stochastic optimization problems by transforming them into deterministic ones. We use quasi-Newton methods and line search to solve each deterministic optimization problem and present a heuristic policy to automate hyperparameter selection. Our experiments show that our method simplifies the VI problem and achieves faster performance than existing methods.

U-Statistics for Importance-Weighted Variational Inference

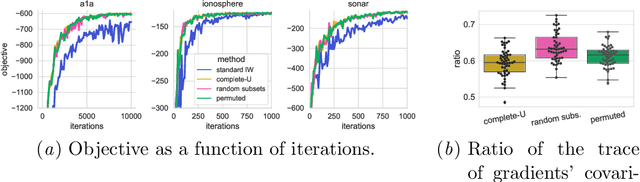
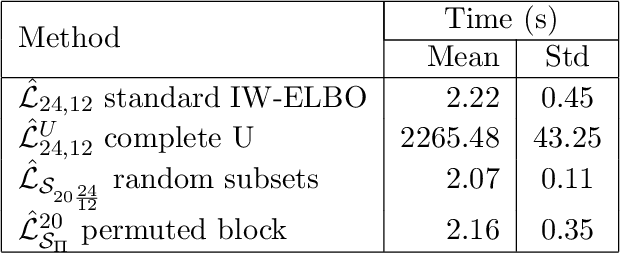
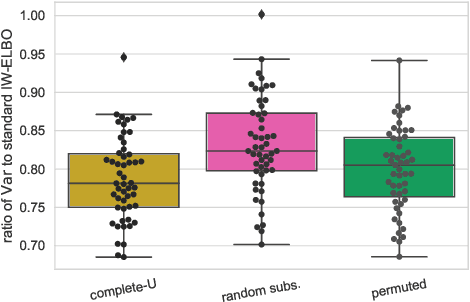
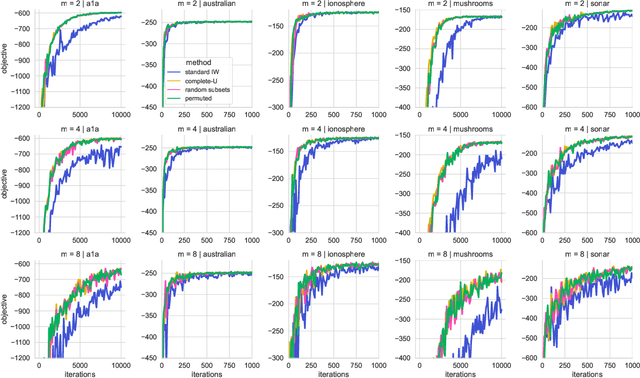
We propose the use of U-statistics to reduce variance for gradient estimation in importance-weighted variational inference. The key observation is that, given a base gradient estimator that requires $m > 1$ samples and a total of $n > m$ samples to be used for estimation, lower variance is achieved by averaging the base estimator on overlapping batches of size $m$ than disjoint batches, as currently done. We use classical U-statistic theory to analyze the variance reduction, and propose novel approximations with theoretical guarantees to ensure computational efficiency. We find empirically that U-statistic variance reduction can lead to modest to significant improvements in inference performance on a range of models, with little computational cost.