Disentangling impact of capacity, objective, batchsize, estimators, and step-size on flow VI

Normalizing flow-based variational inference (flow VI) is a promising approximate inference approach, but its performance remains inconsistent across studies. Numerous algorithmic choices influence flow VI's performance. We conduct a step-by-step analysis to disentangle the impact of some of the key factors: capacity, objectives, gradient estimators, number of gradient estimates (batchsize), and step-sizes. Each step examines one factor while neutralizing others using insights from the previous steps and/or using extensive parallel computation. To facilitate high-fidelity evaluation, we curate a benchmark of synthetic targets that represent common posterior pathologies and allow for exact sampling. We provide specific recommendations for different factors and propose a flow VI recipe that matches or surpasses leading turnkey Hamiltonian Monte Carlo (HMC) methods.

Understanding and mitigating difficulties in posterior predictive evaluation

Predictive posterior densities (PPDs) are of interest in approximate Bayesian inference. Typically, these are estimated by simple Monte Carlo (MC) averages using samples from the approximate posterior. We observe that the signal-to-noise ratio (SNR) of such estimators can be extremely low. An analysis for exact inference reveals SNR decays exponentially as there is an increase in (a) the mismatch between training and test data, (b) the dimensionality of the latent space, or (c) the size of the test data relative to the training data. Further analysis extends these results to approximate inference. To remedy the low SNR problem, we propose replacing simple MC sampling with importance sampling using a proposal distribution optimized at test time on a variational proxy for the SNR and demonstrate that this yields greatly improved estimates.

Can AI Models Appreciate Document Aesthetics? An Exploration of Legibility and Layout Quality in Relation to Prediction Confidence

A well-designed document communicates not only through its words but also through its visual eloquence. Authors utilize aesthetic elements such as colors, fonts, graphics, and layouts to shape the perception of information. Thoughtful document design, informed by psychological insights, enhances both the visual appeal and the comprehension of the content. While state-of-the-art document AI models demonstrate the benefits of incorporating layout and image data, it remains unclear whether the nuances of document aesthetics are effectively captured. To bridge the gap between human cognition and AI interpretation of aesthetic elements, we formulated hypotheses concerning AI behavior in document understanding tasks, specifically anchored in document design principles. With a focus on legibility and layout quality, we tested four aspects of aesthetic effects: noise, font-size contrast, alignment, and complexity, on model confidence using correlational analysis. The results and observations highlight the value of model analysis rooted in document design theories. Our work serves as a trailhead for further studies and we advocate for continued research in this topic to deepen our understanding of how AI interprets document aesthetics.

Extracting Complex Named Entities in Legal Documents via Weakly Supervised Object Detection

Accurate Named Entity Recognition (NER) is crucial for various information retrieval tasks in industry. However, despite significant progress in traditional NER methods, the extraction of Complex Named Entities remains a relatively unexplored area. In this paper, we propose a novel system that combines object detection for Document Layout Analysis (DLA) with weakly supervised learning to address the challenge of extracting discontinuous complex named entities in legal documents. Notably, to the best of our knowledge, this is the first work to apply weak supervision to DLA. Our experimental results show that the model trained solely on pseudo labels outperforms the supervised baseline when gold-standard data is limited, highlighting the effectiveness of our proposed approach in reducing the dependency on annotated data.

Amortized Variational Inference for Simple Hierarchical Models

It is difficult to use subsampling with variational inference in hierarchical models since the number of local latent variables scales with the dataset. Thus, inference in hierarchical models remains a challenge at large scale. It is helpful to use a variational family with structure matching the posterior, but optimization is still slow due to the huge number of local distributions. Instead, this paper suggests an amortized approach where shared parameters simultaneously represent all local distributions. This approach is similarly accurate as using a given joint distribution (e.g., a full-rank Gaussian) but is feasible on datasets that are several orders of magnitude larger. It is also dramatically faster than using a structured variational distribution.

Normalizing Flows Across Dimensions

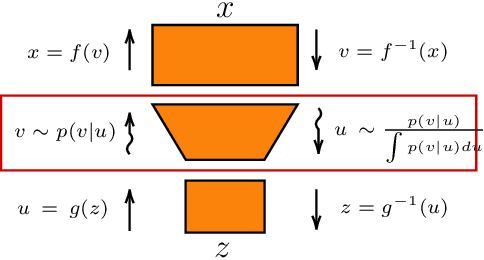
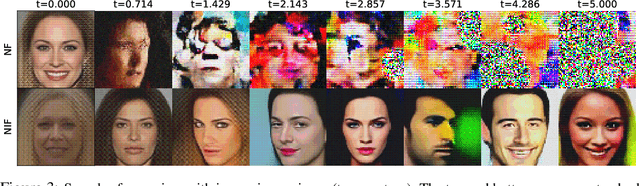
Real-world data with underlying structure, such as pictures of faces, are hypothesized to lie on a low-dimensional manifold. This manifold hypothesis has motivated state-of-the-art generative algorithms that learn low-dimensional data representations. Unfortunately, a popular generative model, normalizing flows, cannot take advantage of this. Normalizing flows are based on successive variable transformations that are, by design, incapable of learning lower-dimensional representations. In this paper we introduce noisy injective flows (NIF), a generalization of normalizing flows that can go across dimensions. NIF explicitly map the latent space to a learnable manifold in a high-dimensional data space using injective transformations. We further employ an additive noise model to account for deviations from the manifold and identify a stochastic inverse of the generative process. Empirically, we demonstrate that a simple application of our method to existing flow architectures can significantly improve sample quality and yield separable data embeddings.

Advances in Black-Box VI: Normalizing Flows, Importance Weighting, and Optimization

Recent research has seen several advances relevant to black-box VI, but the current state of automatic posterior inference is unclear. One such advance is the use of normalizing flows to define flexible posterior densities for deep latent variable models. Another direction is the integration of Monte-Carlo methods to serve two purposes; first, to obtain tighter variational objectives for optimization, and second, to define enriched variational families through sampling. However, both flows and variational Monte-Carlo methods remain relatively unexplored for black-box VI. Moreover, on a pragmatic front, there are several optimization considerations like step-size scheme, parameter initialization, and choice of gradient estimators, for which there are no clear guidance in the existing literature. In this paper, we postulate that black-box VI is best addressed through a careful combination of numerous algorithmic components. We evaluate components relating to optimization, flows, and Monte-Carlo methods on a benchmark of 30 models from the Stan model library. The combination of these algorithmic components significantly advances the state-of-the-art "out of the box" variational inference.