Disentanglement Beyond Generative Models with Riemannian ICA

There is a gap between the theoretical foundations of disentanglement and the practice of modern representation learning. Existing theoretical frameworks, particularly Independent Component Analysis (ICA) and its nonlinear variants, assume a generative model with statistically independent latent variables underlying the data so that disentanglement amounts to identifying the latents that could have generated the data. This generative framework is interpretable and theoretically justified, but its strong assumptions make it difficult to apply to modern representation learning. Modern pretrained encoders often learn features that exhibit disentangled properties without making generative assumptions, yet there is no general theory for interpreting these features as independent factors of variation. We take a step toward such a theory by introducing Riemannian ICA (RICA), which replaces ICA's global generative model with local geometric structure. RICA is founded on the observation that in ICA, the factors of variation underlying a data point can be understood through radial curves emanating from the point that map to axis-aligned lines in the latent space. We formalize this perspective using Riemannian geometry and introduce our theory in a way that is consistent with the existing generative approach. Our main contribution is the disentanglement tensor, which encodes a second-order notion of disentanglement that we call pointwise disentanglement. This tensor depends on the Hessian of the data log likelihood as well as the Ricci curvature induced by the model. In a controlled source recovery setting with known ground-truth sources, RICA recovers sources across several manifolds, while the success of ICA baselines depends on the coordinates used to represent the observations. Our work provides a theoretical basis for studying local disentanglement without assuming a global generative model.

Principal Manifold Flows

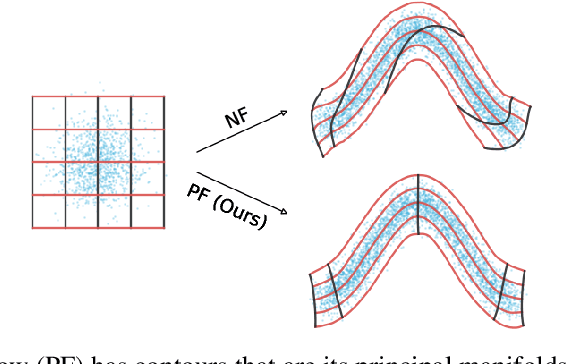
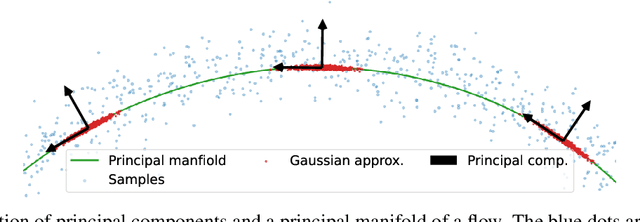
Normalizing flows map an independent set of latent variables to their samples using a bijective transformation. Despite the exact correspondence between samples and latent variables, their high level relationship is not well understood. In this paper we characterize the geometric structure of flows using principal manifolds and understand the relationship between latent variables and samples using contours. We introduce a novel class of normalizing flows, called principal manifold flows (PF), whose contours are its principal manifolds, and a variant for injective flows (iPF) that is more efficient to train than regular injective flows. PFs can be constructed using any flow architecture, are trained with a regularized maximum likelihood objective and can perform density estimation on all of their principal manifolds. In our experiments we show that PFs and iPFs are able to learn the principal manifolds over a variety of datasets. Additionally, we show that PFs can perform density estimation on data that lie on a manifold with variable dimensionality, which is not possible with existing normalizing flows.

Normalizing Flows Across Dimensions

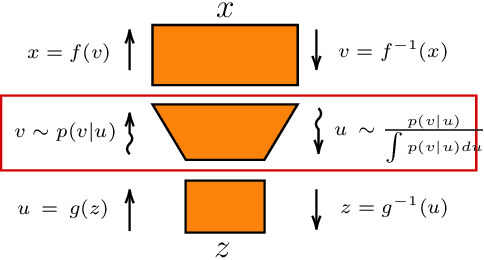
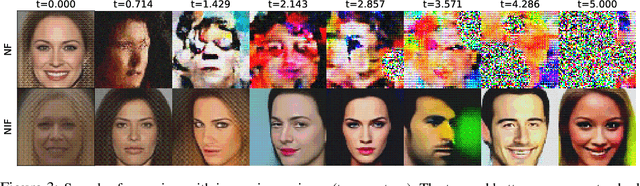
Real-world data with underlying structure, such as pictures of faces, are hypothesized to lie on a low-dimensional manifold. This manifold hypothesis has motivated state-of-the-art generative algorithms that learn low-dimensional data representations. Unfortunately, a popular generative model, normalizing flows, cannot take advantage of this. Normalizing flows are based on successive variable transformations that are, by design, incapable of learning lower-dimensional representations. In this paper we introduce noisy injective flows (NIF), a generalization of normalizing flows that can go across dimensions. NIF explicitly map the latent space to a learnable manifold in a high-dimensional data space using injective transformations. We further employ an additive noise model to account for deviations from the manifold and identify a stochastic inverse of the generative process. Empirically, we demonstrate that a simple application of our method to existing flow architectures can significantly improve sample quality and yield separable data embeddings.

Explainable Genetic Inheritance Pattern Prediction

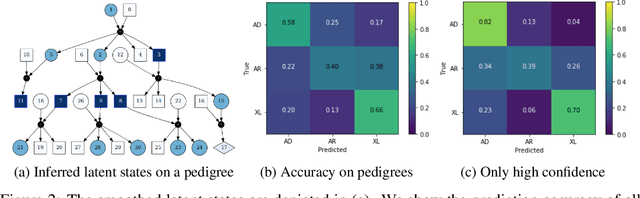
Diagnosing an inherited disease often requires identifying the pattern of inheritance in a patient's family. We represent family trees with genetic patterns of inheritance using hypergraphs and latent state space models to provide explainable inheritance pattern predictions. Our approach allows for exact causal inference over a patient's possible genotypes given their relatives' phenotypes. By design, inference can be examined at a low level to provide explainable predictions. Furthermore, we make use of human intuition by providing a method to assign hypothetical evidence to any inherited gene alleles. Our analysis supports the application of latent state space models to improve patient care in cases of rare inherited diseases where access to genetic specialists is limited.