Resource-Constrained Heuristic for Max-SAT

We propose a resource-constrained heuristic for instances of Max-SAT that iteratively decomposes a larger problem into smaller subcomponents that can be solved by optimized solvers and hardware. The unconstrained outer loop maintains the state space of a given problem and selects a subset of the SAT variables for optimization independent of previous calls. The resource-constrained inner loop maximizes the number of satisfiable clauses in the "sub-SAT" problem. Our outer loop is agnostic to the mechanisms of the inner loop, allowing for the use of traditional solvers for the optimization step. However, we can also transform the selected "sub-SAT" problem into a quadratic unconstrained binary optimization (QUBO) one and use specialized hardware for optimization. In contrast to existing solutions that convert a SAT instance into a QUBO one before decomposition, we choose a subset of the SAT variables before QUBO optimization. We analyze a set of variable selection methods, including a novel graph-based method that exploits the structure of a given SAT instance. The number of QUBO variables needed to encode a (sub-)SAT problem varies, so we additionally learn a model that predicts the size of sub-SAT problems that will fit a fixed-size QUBO solver. We empirically demonstrate our results on a set of randomly generated Max-SAT instances as well as real world examples from the Max-SAT evaluation benchmarks and outperform existing QUBO decomposer solutions.

On Sequential Bayesian Inference for Continual Learning

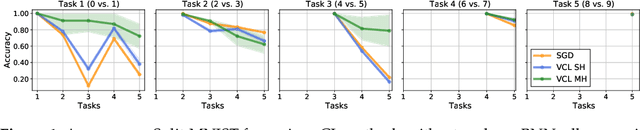
Sequential Bayesian inference can be used for continual learning to prevent catastrophic forgetting of past tasks and provide an informative prior when learning new tasks. We revisit sequential Bayesian inference and test whether having access to the true posterior is guaranteed to prevent catastrophic forgetting in Bayesian neural networks. To do this we perform sequential Bayesian inference using Hamiltonian Monte Carlo. We propagate the posterior as a prior for new tasks by fitting a density estimator on Hamiltonian Monte Carlo samples. We find that this approach fails to prevent catastrophic forgetting demonstrating the difficulty in performing sequential Bayesian inference in neural networks. From there we study simple analytical examples of sequential Bayesian inference and CL and highlight the issue of model misspecification which can lead to sub-optimal continual learning performance despite exact inference. Furthermore, we discuss how task data imbalances can cause forgetting. From these limitations, we argue that we need probabilistic models of the continual learning generative process rather than relying on sequential Bayesian inference over Bayesian neural network weights. In this vein, we also propose a simple baseline called Prototypical Bayesian Continual Learning, which is competitive with state-of-the-art Bayesian continual learning methods on class incremental continual learning vision benchmarks.

Principal Manifold Flows

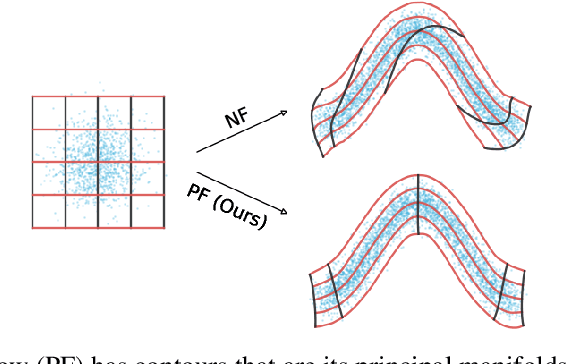
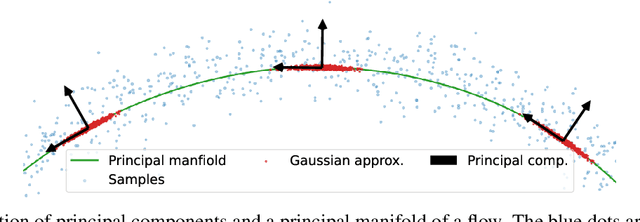
Normalizing flows map an independent set of latent variables to their samples using a bijective transformation. Despite the exact correspondence between samples and latent variables, their high level relationship is not well understood. In this paper we characterize the geometric structure of flows using principal manifolds and understand the relationship between latent variables and samples using contours. We introduce a novel class of normalizing flows, called principal manifold flows (PF), whose contours are its principal manifolds, and a variant for injective flows (iPF) that is more efficient to train than regular injective flows. PFs can be constructed using any flow architecture, are trained with a regularized maximum likelihood objective and can perform density estimation on all of their principal manifolds. In our experiments we show that PFs and iPFs are able to learn the principal manifolds over a variety of datasets. Additionally, we show that PFs can perform density estimation on data that lie on a manifold with variable dimensionality, which is not possible with existing normalizing flows.

Decentralized Bayesian Learning with Metropolis-Adjusted Hamiltonian Monte Carlo

Federated learning performed by a decentralized networks of agents is becoming increasingly important with the prevalence of embedded software on autonomous devices. Bayesian approaches to learning benefit from offering more information as to the uncertainty of a random quantity, and Langevin and Hamiltonian methods are effective at realizing sampling from an uncertain distribution with large parameter dimensions. Such methods have only recently appeared in the decentralized setting, and either exclusively use stochastic gradient Langevin and Hamiltonian Monte Carlo approaches that require a diminishing stepsize to asymptotically sample from the posterior and are known in practice to characterize uncertainty less faithfully than constant step-size methods with a Metropolis adjustment, or assume strong convexity properties of the potential function. We present the first approach to incorporating constant stepsize Metropolis-adjusted HMC in the decentralized sampling framework, show theoretical guarantees for consensus and probability distance to the posterior stationary distribution, and demonstrate their effectiveness numerically on standard real world problems, including decentralized learning of neural networks which is known to be highly non-convex.

Inferring agent objectives at different scales of a complex adaptive system

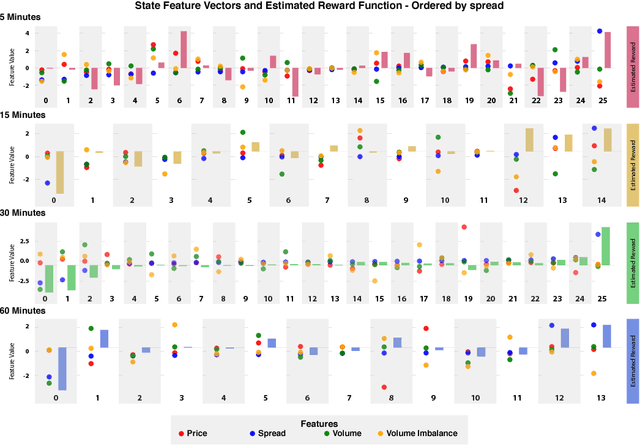
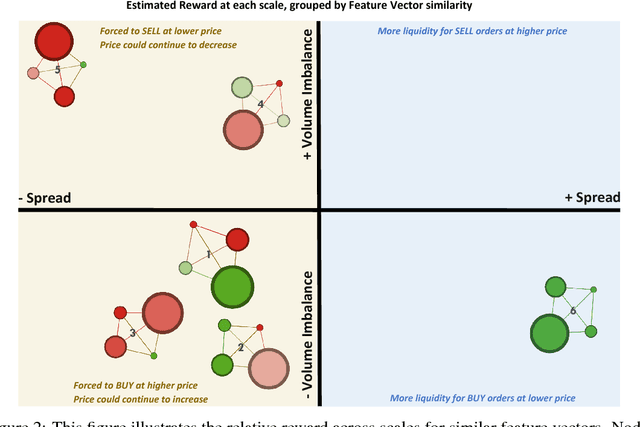
We introduce a framework to study the effective objectives at different time scales of financial market microstructure. The financial market can be regarded as a complex adaptive system, where purposeful agents collectively and simultaneously create and perceive their environment as they interact with it. It has been suggested that multiple agent classes operate in this system, with a non-trivial hierarchy of top-down and bottom-up causation classes with different effective models governing each level. We conjecture that agent classes may in fact operate at different time scales and thus act differently in response to the same perceived market state. Given scale-specific temporal state trajectories and action sequences estimated from aggregate market behaviour, we use Inverse Reinforcement Learning to compute the effective reward function for the aggregate agent class at each scale, allowing us to assess the relative attractiveness of feature vectors across different scales. Differences in reward functions for feature vectors may indicate different objectives of market participants, which could assist in finding the scale boundary for agent classes. This has implications for learning algorithms operating in this domain.