Calibrating Uncertainty Quantification of Multi-Modal LLMs using Grounding

We introduce a novel approach for calibrating uncertainty quantification (UQ) tailored for multi-modal large language models (LLMs). Existing state-of-the-art UQ methods rely on consistency among multiple responses generated by the LLM on an input query under diverse settings. However, these approaches often report higher confidence in scenarios where the LLM is consistently incorrect. This leads to a poorly calibrated confidence with respect to accuracy. To address this, we leverage cross-modal consistency in addition to self-consistency to improve the calibration of the multi-modal models. Specifically, we ground the textual responses to the visual inputs. The confidence from the grounding model is used to calibrate the overall confidence. Given that using a grounding model adds its own uncertainty in the pipeline, we apply temperature scaling - a widely accepted parametric calibration technique - to calibrate the grounding model's confidence in the accuracy of generated responses. We evaluate the proposed approach across multiple multi-modal tasks, such as medical question answering (Slake) and visual question answering (VQAv2), considering multi-modal models such as LLaVA-Med and LLaVA. The experiments demonstrate that the proposed framework achieves significantly improved calibration on both tasks.

Melanoma Detection with Uncertainty Quantification

Early detection of melanoma is crucial for improving survival rates. Current detection tools often utilize data-driven machine learning methods but often overlook the full integration of multiple datasets. We combine publicly available datasets to enhance data diversity, allowing numerous experiments to train and evaluate various classifiers. We then calibrate them to minimize misdiagnoses by incorporating uncertainty quantification. Our experiments on benchmark datasets show accuracies of up to 93.2% before and 97.8% after applying uncertainty-based rejection, leading to a reduction in misdiagnoses by over 40.5%. Our code and data are publicly available, and a web-based interface for quick melanoma detection of user-supplied images is also provided.

Addressing Uncertainty in LLMs to Enhance Reliability in Generative AI

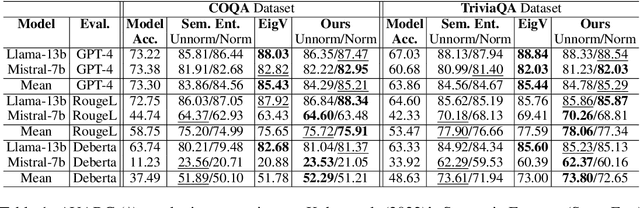
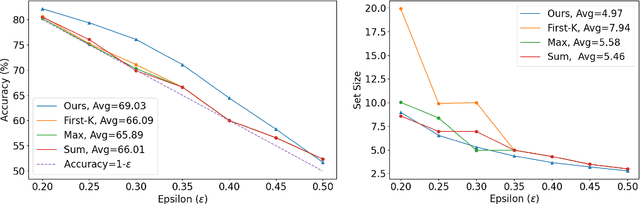
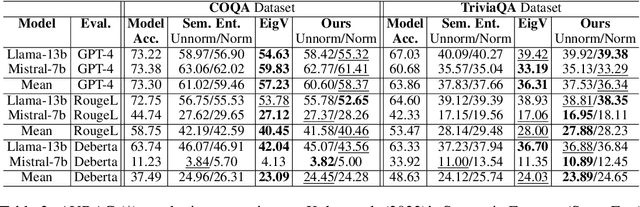
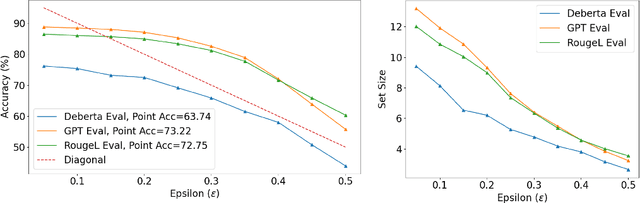
In this paper, we present a dynamic semantic clustering approach inspired by the Chinese Restaurant Process, aimed at addressing uncertainty in the inference of Large Language Models (LLMs). We quantify uncertainty of an LLM on a given query by calculating entropy of the generated semantic clusters. Further, we propose leveraging the (negative) likelihood of these clusters as the (non)conformity score within Conformal Prediction framework, allowing the model to predict a set of responses instead of a single output, thereby accounting for uncertainty in its predictions. We demonstrate the effectiveness of our uncertainty quantification (UQ) technique on two well known question answering benchmarks, COQA and TriviaQA, utilizing two LLMs, Llama2 and Mistral. Our approach achieves SOTA performance in UQ, as assessed by metrics such as AUROC, AUARC, and AURAC. The proposed conformal predictor is also shown to produce smaller prediction sets while maintaining the same probabilistic guarantee of including the correct response, in comparison to existing SOTA conformal prediction baseline.

Resource-Constrained Heuristic for Max-SAT

We propose a resource-constrained heuristic for instances of Max-SAT that iteratively decomposes a larger problem into smaller subcomponents that can be solved by optimized solvers and hardware. The unconstrained outer loop maintains the state space of a given problem and selects a subset of the SAT variables for optimization independent of previous calls. The resource-constrained inner loop maximizes the number of satisfiable clauses in the "sub-SAT" problem. Our outer loop is agnostic to the mechanisms of the inner loop, allowing for the use of traditional solvers for the optimization step. However, we can also transform the selected "sub-SAT" problem into a quadratic unconstrained binary optimization (QUBO) one and use specialized hardware for optimization. In contrast to existing solutions that convert a SAT instance into a QUBO one before decomposition, we choose a subset of the SAT variables before QUBO optimization. We analyze a set of variable selection methods, including a novel graph-based method that exploits the structure of a given SAT instance. The number of QUBO variables needed to encode a (sub-)SAT problem varies, so we additionally learn a model that predicts the size of sub-SAT problems that will fit a fixed-size QUBO solver. We empirically demonstrate our results on a set of randomly generated Max-SAT instances as well as real world examples from the Max-SAT evaluation benchmarks and outperform existing QUBO decomposer solutions.

Direct Amortized Likelihood Ratio Estimation

We introduce a new amortized likelihood ratio estimator for likelihood-free simulation-based inference (SBI). Our estimator is simple to train and estimates the likelihood ratio using a single forward pass of the neural estimator. Our approach directly computes the likelihood ratio between two competing parameter sets which is different from the previous approach of comparing two neural network output values. We refer to our model as the direct neural ratio estimator (DNRE). As part of introducing the DNRE, we derive a corresponding Monte Carlo estimate of the posterior. We benchmark our new ratio estimator and compare to previous ratio estimators in the literature. We show that our new ratio estimator often outperforms these previous approaches. As a further contribution, we introduce a new derivative estimator for likelihood ratio estimators that enables us to compare likelihood-free Hamiltonian Monte Carlo (HMC) with random-walk Metropolis-Hastings (MH). We show that HMC is equally competitive, which has not been previously shown. Finally, we include a novel real-world application of SBI by using our neural ratio estimator to design a quadcopter. Code is available at https://github.com/SRI-CSL/dnre.

AxonEM Dataset: 3D Axon Instance Segmentation of Brain Cortical Regions

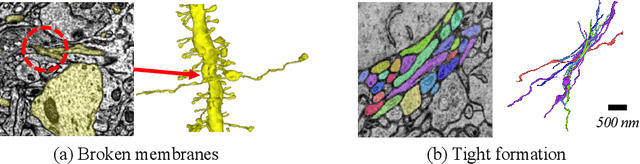
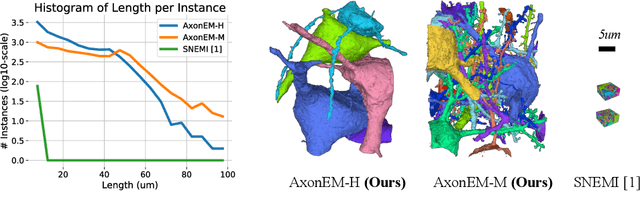
Electron microscopy (EM) enables the reconstruction of neural circuits at the level of individual synapses, which has been transformative for scientific discoveries. However, due to the complex morphology, an accurate reconstruction of cortical axons has become a major challenge. Worse still, there is no publicly available large-scale EM dataset from the cortex that provides dense ground truth segmentation for axons, making it difficult to develop and evaluate large-scale axon reconstruction methods. To address this, we introduce the AxonEM dataset, which consists of two 30x30x30 um^3 EM image volumes from the human and mouse cortex, respectively. We thoroughly proofread over 18,000 axon instances to provide dense 3D axon instance segmentation, enabling large-scale evaluation of axon reconstruction methods. In addition, we densely annotate nine ground truth subvolumes for training, per each data volume. With this, we reproduce two published state-of-the-art methods and provide their evaluation results as a baseline. We publicly release our code and data at https://connectomics-bazaar.github.io/proj/AxonEM/index.html to foster the development of advanced methods.

Anisotropic EM Segmentation by 3D Affinity Learning and Agglomeration

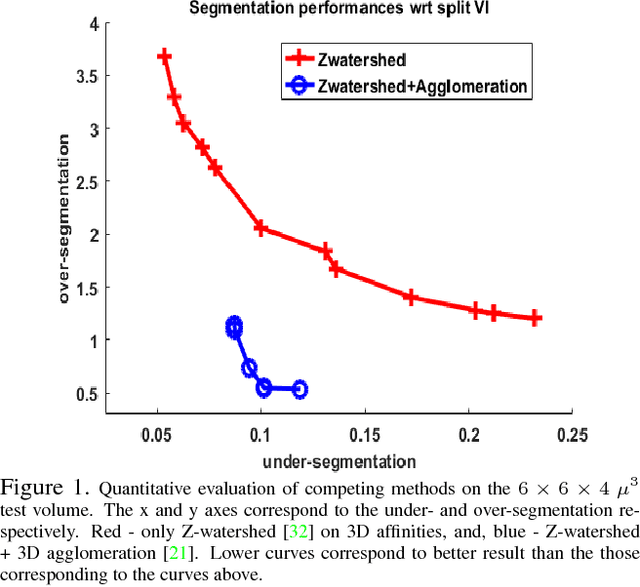
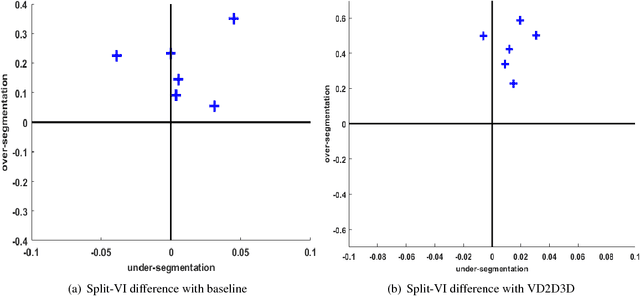
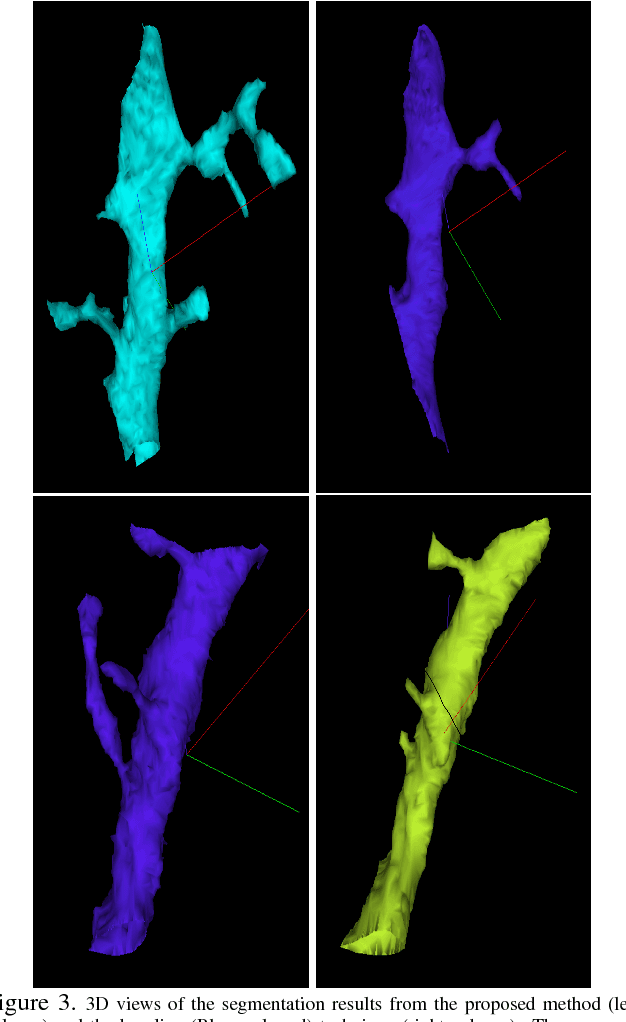
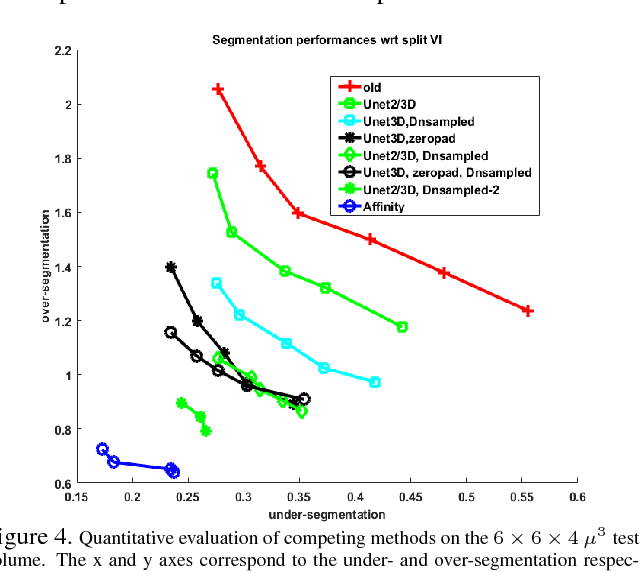
The field of connectomics has recently produced neuron wiring diagrams from relatively large brain regions from multiple animals. Most of these neural reconstructions were computed from isotropic (e.g., FIBSEM) or near isotropic (e.g., SBEM) data. In spite of the remarkable progress on algorithms in recent years, automatic dense reconstruction from anisotropic data remains a challenge for the connectomics community. One significant hurdle in the segmentation of anisotropic data is the difficulty in generating a suitable initial over-segmentation. In this study, we present a segmentation method for anisotropic EM data that agglomerates a 3D over-segmentation computed from the 3D affinity prediction. A 3D U-net is trained to predict 3D affinities by the MALIS approach. Experiments on multiple datasets demonstrates the strength and robustness of the proposed method for anisotropic EM segmentation.