ActiveInitSplat: How Active Image Selection Helps Gaussian Splatting

Gaussian splatting (GS) along with its extensions and variants provides outstanding performance in real-time scene rendering while meeting reduced storage demands and computational efficiency. While the selection of 2D images capturing the scene of interest is crucial for the proper initialization and training of GS, hence markedly affecting the rendering performance, prior works rely on passively and typically densely selected 2D images. In contrast, this paper proposes `ActiveInitSplat', a novel framework for active selection of training images for proper initialization and training of GS. ActiveInitSplat relies on density and occupancy criteria of the resultant 3D scene representation from the selected 2D images, to ensure that the latter are captured from diverse viewpoints leading to better scene coverage and that the initialized Gaussian functions are well aligned with the actual 3D structure. Numerical tests on well-known simulated and real environments demonstrate the merits of ActiveInitSplat resulting in significant GS rendering performance improvement over passive GS baselines, in the widely adopted LPIPS, SSIM, and PSNR metrics.

Active Sampling and Gaussian Reconstruction for Radio Frequency Radiance Field

Radio-frequency (RF) Radiance Field reconstruction is a challenging problem. The difficulty lies in the interactions between the propagating signal and objects, such as reflections and diffraction, which are hard to model precisely, especially when the shapes and materials of the objects are unknown. Previously, a neural network-based method was proposed to reconstruct the RF Radiance Field, showing promising results. However, this neural network-based method has some limitations: it requires a large number of samples for training and is computationally expensive. Additionally, the neural network only provides the predicted mean of the RF Radiance Field and does not offer an uncertainty model. In this work, we propose a training-free Gaussian reconstruction method for RF Radiance Field. Our method demonstrates that the required number of samples is significantly smaller compared to the neural network-based approach. Furthermore, we introduce an uncertainty model that provides confidence estimates for predictions at any selected position in the scene. We also combine the Gaussian reconstruction method with active sampling, which further reduces the number of samples needed to achieve the same performance. Finally, we explore the potential benefits of our method in a quasi-dynamic setting, showcasing its ability to adapt to changes in the scene without requiring the entire process to be repeated.

Trojan Cleansing with Neural Collapse

Trojan attacks are sophisticated training-time attacks on neural networks that embed backdoor triggers which force the network to produce a specific output on any input which includes the trigger. With the increasing relevance of deep networks which are too large to train with personal resources and which are trained on data too large to thoroughly audit, these training-time attacks pose a significant risk. In this work, we connect trojan attacks to Neural Collapse, a phenomenon wherein the final feature representations of over-parameterized neural networks converge to a simple geometric structure. We provide experimental evidence that trojan attacks disrupt this convergence for a variety of datasets and architectures. We then use this disruption to design a lightweight, broadly generalizable mechanism for cleansing trojan attacks from a wide variety of different network architectures and experimentally demonstrate its efficacy.

Coverage Analysis for Digital Cousin Selection -- Improving Multi-Environment Q-Learning

Q-learning is widely employed for optimizing various large-dimensional networks with unknown system dynamics. Recent advancements include multi-environment mixed Q-learning (MEMQ) algorithms, which utilize multiple independent Q-learning algorithms across multiple, structurally related but distinct environments and outperform several state-of-the-art Q-learning algorithms in terms of accuracy, complexity, and robustness. We herein conduct a comprehensive probabilistic coverage analysis to ensure optimal data coverage conditions for MEMQ algorithms. First, we derive upper and lower bounds on the expectation and variance of different coverage coefficients (CC) for MEMQ algorithms. Leveraging these bounds, we develop a simple way of comparing the utilities of multiple environments in MEMQ algorithms. This approach appears to be near optimal versus our previously proposed partial ordering approach. We also present a novel CC-based MEMQ algorithm to improve the accuracy and complexity of existing MEMQ algorithms. Numerical experiments are conducted using random network graphs with four different graph properties. Our algorithm can reduce the average policy error (APE) by 65% compared to partial ordering and is 95% faster than the exhaustive search. It also achieves 60% less APE than several state-of-the-art reinforcement learning and prior MEMQ algorithms. Additionally, we numerically verify the theoretical results and show their scalability with the action-space size.

Primal-Dual Continual Learning: Stability and Plasticity through Lagrange Multipliers

Continual learning is inherently a constrained learning problem. The goal is to learn a predictor under a \emph{no-forgetting} requirement. Although several prior studies formulate it as such, they do not solve the constrained problem explicitly. In this work, we show that it is both possible and beneficial to undertake the constrained optimization problem directly. To do this, we leverage recent results in constrained learning through Lagrangian duality. We focus on memory-based methods, where a small subset of samples from previous tasks can be stored in a replay buffer. In this setting, we analyze two versions of the continual learning problem: a coarse approach with constraints at the task level and a fine approach with constraints at the sample level. We show that dual variables indicate the sensitivity of the optimal value with respect to constraint perturbations. We then leverage this result to partition the buffer in the coarse approach, allocating more resources to harder tasks, and to populate the buffer in the fine approach, including only impactful samples. We derive sub-optimality bounds, and empirically corroborate our theoretical results in various continual learning benchmarks. We also discuss the limitations of these methods with respect to the amount of memory available and the number of constraints involved in the optimization problem.

SABRE: Robust Bayesian Peer-to-Peer Federated Learning

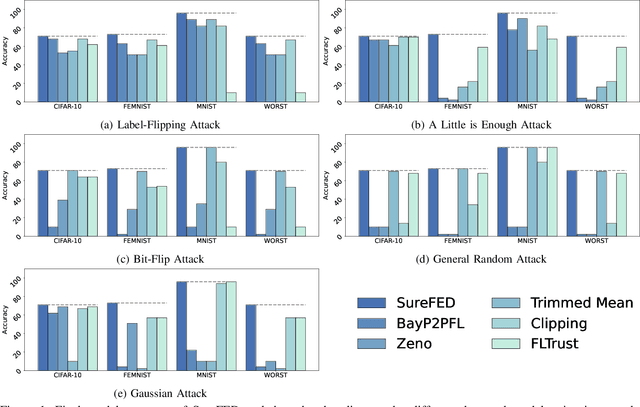
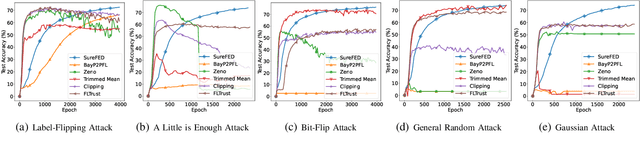
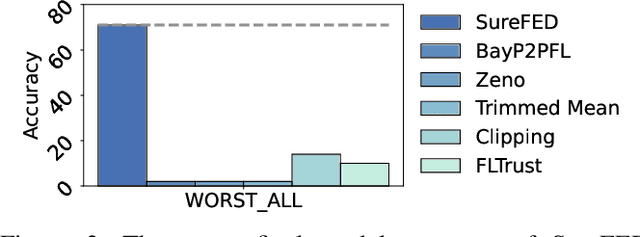
We introduce SABRE, a novel framework for robust variational Bayesian peer-to-peer federated learning. We analyze the robustness of the known variational Bayesian peer-to-peer federated learning framework (BayP2PFL) against poisoning attacks and subsequently show that BayP2PFL is not robust against those attacks. The new SABRE aggregation methodology is then devised to overcome the limitations of the existing frameworks. SABRE works well in non-IID settings, does not require the majority of the benign nodes over the compromised ones, and even outperforms the baseline algorithm in benign settings. We theoretically prove the robustness of our algorithm against data / model poisoning attacks in a decentralized linear regression setting. Proof-of-Concept evaluations on benchmark data from image classification demonstrate the superiority of SABRE over the existing frameworks under various poisoning attacks.

Decentralized Competing Bandits in Non-Stationary Matching Markets

Understanding complex dynamics of two-sided online matching markets, where the demand-side agents compete to match with the supply-side (arms), has recently received substantial interest. To that end, in this paper, we introduce the framework of decentralized two-sided matching market under non stationary (dynamic) environments. We adhere to the serial dictatorship setting, where the demand-side agents have unknown and different preferences over the supply-side (arms), but the arms have fixed and known preference over the agents. We propose and analyze a decentralized and asynchronous learning algorithm, namely Decentralized Non-stationary Competing Bandits (\texttt{DNCB}), where the agents play (restrictive) successive elimination type learning algorithms to learn their preference over the arms. The complexity in understanding such a system stems from the fact that the competing bandits choose their actions in an asynchronous fashion, and the lower ranked agents only get to learn from a set of arms, not \emph{dominated} by the higher ranked agents, which leads to \emph{forced exploration}. With carefully defined complexity parameters, we characterize this \emph{forced exploration} and obtain sub-linear (logarithmic) regret of \texttt{DNCB}. Furthermore, we validate our theoretical findings via experiments.

Instance-Dependent Regret Analysis of Kernelized Bandits

We study the kernelized bandit problem, that involves designing an adaptive strategy for querying a noisy zeroth-order-oracle to efficiently learn about the optimizer of an unknown function $f$ with a norm bounded by $M<\infty$ in a Reproducing Kernel Hilbert Space~(RKHS) associated with a positive definite kernel $K$. Prior results, working in a \emph{minimax framework}, have characterized the worst-case~(over all functions in the problem class) limits on regret achievable by \emph{any} algorithm, and have constructed algorithms with matching~(modulo polylogarithmic factors) worst-case performance for the \matern family of kernels. These results suffer from two drawbacks. First, the minimax lower bound gives no information about the limits of regret achievable by the commonly used algorithms on specific problem instances. Second, due to their worst-case nature, the existing upper bound analysis fails to adapt to easier problem instances within the function class. Our work takes steps to address both these issues. First, we derive \emph{instance-dependent} regret lower bounds for algorithms with uniformly~(over the function class) vanishing normalized cumulative regret. Our result, valid for all the practically relevant kernelized bandits algorithms, such as, GP-UCB, GP-TS and SupKernelUCB, identifies a fundamental complexity measure associated with every problem instance. We then address the second issue, by proposing a new minimax near-optimal algorithm which also adapts to easier problem instances.

Open Problem: Tight Online Confidence Intervals for RKHS Elements

Confidence intervals are a crucial building block in the analysis of various online learning problems. The analysis of kernel based bandit and reinforcement learning problems utilize confidence intervals applicable to the elements of a reproducing kernel Hilbert space (RKHS). However, the existing confidence bounds do not appear to be tight, resulting in suboptimal regret bounds. In fact, the existing regret bounds for several kernelized bandit algorithms (e.g., GP-UCB, GP-TS, and their variants) may fail to even be sublinear. It is unclear whether the suboptimal regret bound is a fundamental shortcoming of these algorithms or an artifact of the proof, and the main challenge seems to stem from the online (sequential) nature of the observation points. We formalize the question of online confidence intervals in the RKHS setting and overview the existing results.

Trojan Signatures in DNN Weights

Deep neural networks have been shown to be vulnerable to backdoor, or trojan, attacks where an adversary has embedded a trigger in the network at training time such that the model correctly classifies all standard inputs, but generates a targeted, incorrect classification on any input which contains the trigger. In this paper, we present the first ultra light-weight and highly effective trojan detection method that does not require access to the training/test data, does not involve any expensive computations, and makes no assumptions on the nature of the trojan trigger. Our approach focuses on analysis of the weights of the final, linear layer of the network. We empirically demonstrate several characteristics of these weights that occur frequently in trojaned networks, but not in benign networks. In particular, we show that the distribution of the weights associated with the trojan target class is clearly distinguishable from the weights associated with other classes. Using this, we demonstrate the effectiveness of our proposed detection method against state-of-the-art attacks across a variety of architectures, datasets, and trigger types.