Shubhanshu Shekhar
Deep anytime-valid hypothesis testing
Oct 30, 2023



Abstract:We propose a general framework for constructing powerful, sequential hypothesis tests for a large class of nonparametric testing problems. The null hypothesis for these problems is defined in an abstract form using the action of two known operators on the data distribution. This abstraction allows for a unified treatment of several classical tasks, such as two-sample testing, independence testing, and conditional-independence testing, as well as modern problems, such as testing for adversarial robustness of machine learning (ML) models. Our proposed framework has the following advantages over classical batch tests: 1) it continuously monitors online data streams and efficiently aggregates evidence against the null, 2) it provides tight control over the type I error without the need for multiple testing correction, 3) it adapts the sample size requirement to the unknown hardness of the problem. We develop a principled approach of leveraging the representation capability of ML models within the testing-by-betting framework, a game-theoretic approach for designing sequential tests. Empirical results on synthetic and real-world datasets demonstrate that tests instantiated using our general framework are competitive against specialized baselines on several tasks.
On the near-optimality of betting confidence sets for bounded means
Oct 02, 2023

Abstract:Constructing nonasymptotic confidence intervals (CIs) for the mean of a univariate distribution from independent and identically distributed (i.i.d.) observations is a fundamental task in statistics. For bounded observations, a classical nonparametric approach proceeds by inverting standard concentration bounds, such as Hoeffding's or Bernstein's inequalities. Recently, an alternative betting-based approach for defining CIs and their time-uniform variants called confidence sequences (CSs), has been shown to be empirically superior to the classical methods. In this paper, we provide theoretical justification for this improved empirical performance of betting CIs and CSs. Our main contributions are as follows: (i) We first compare CIs using the values of their first-order asymptotic widths (scaled by $\sqrt{n}$), and show that the betting CI of Waudby-Smith and Ramdas (2023) has a smaller limiting width than existing empirical Bernstein (EB)-CIs. (ii) Next, we establish two lower bounds that characterize the minimum width achievable by any method for constructing CIs/CSs in terms of certain inverse information projections. (iii) Finally, we show that the betting CI and CS match the fundamental limits, modulo an additive logarithmic term and a multiplicative constant. Overall these results imply that the betting CI~(and CS) admit stronger theoretical guarantees than the existing state-of-the-art EB-CI~(and CS); both in the asymptotic and finite-sample regimes.
Reducing sequential change detection to sequential estimation
Sep 16, 2023Abstract:We consider the problem of sequential change detection, where the goal is to design a scheme for detecting any changes in a parameter or functional $\theta$ of the data stream distribution that has small detection delay, but guarantees control on the frequency of false alarms in the absence of changes. In this paper, we describe a simple reduction from sequential change detection to sequential estimation using confidence sequences: we begin a new $(1-\alpha)$-confidence sequence at each time step, and proclaim a change when the intersection of all active confidence sequences becomes empty. We prove that the average run length is at least $1/\alpha$, resulting in a change detection scheme with minimal structural assumptions~(thus allowing for possibly dependent observations, and nonparametric distribution classes), but strong guarantees. Our approach bears an interesting parallel with the reduction from change detection to sequential testing of Lorden (1971) and the e-detector of Shin et al. (2022).
Risk-limiting Financial Audits via Weighted Sampling without Replacement
May 08, 2023Abstract:We introduce the notion of a risk-limiting financial auditing (RLFA): given $N$ transactions, the goal is to estimate the total misstated monetary fraction~($m^*$) to a given accuracy $\epsilon$, with confidence $1-\delta$. We do this by constructing new confidence sequences (CSs) for the weighted average of $N$ unknown values, based on samples drawn without replacement according to a (randomized) weighted sampling scheme. Using the idea of importance weighting to construct test martingales, we first develop a framework to construct CSs for arbitrary sampling strategies. Next, we develop methods to improve the quality of CSs by incorporating side information about the unknown values associated with each item. We show that when the side information is sufficiently predictive, it can directly drive the sampling. Addressing the case where the accuracy is unknown a priori, we introduce a method that incorporates side information via control variates. Crucially, our construction is adaptive: if the side information is highly predictive of the unknown misstated amounts, then the benefits of incorporating it are significant; but if the side information is uncorrelated, our methods learn to ignore it. Our methods recover state-of-the-art bounds for the special case when the weights are equal, which has already found applications in election auditing. The harder weighted case solves our more challenging problem of AI-assisted financial auditing.
Sequential change detection via backward confidence sequences
Feb 06, 2023Abstract:We present a simple reduction from sequential estimation to sequential changepoint detection (SCD). In short, suppose we are interested in detecting changepoints in some parameter or functional $\theta$ of the underlying distribution. We demonstrate that if we can construct a confidence sequence (CS) for $\theta$, then we can also successfully perform SCD for $\theta$. This is accomplished by checking if two CSs -- one forwards and the other backwards -- ever fail to intersect. Since the literature on CSs has been rapidly evolving recently, the reduction provided in this paper immediately solves several old and new change detection problems. Further, our "backward CS", constructed by reversing time, is new and potentially of independent interest. We provide strong nonasymptotic guarantees on the frequency of false alarms and detection delay, and demonstrate numerical effectiveness on several problems.
A Permutation-Free Kernel Independence Test
Dec 18, 2022



Abstract:In nonparametric independence testing, we observe i.i.d.\ data $\{(X_i,Y_i)\}_{i=1}^n$, where $X \in \mathcal{X}, Y \in \mathcal{Y}$ lie in any general spaces, and we wish to test the null that $X$ is independent of $Y$. Modern test statistics such as the kernel Hilbert-Schmidt Independence Criterion (HSIC) and Distance Covariance (dCov) have intractable null distributions due to the degeneracy of the underlying U-statistics. Thus, in practice, one often resorts to using permutation testing, which provides a nonasymptotic guarantee at the expense of recalculating the quadratic-time statistics (say) a few hundred times. This paper provides a simple but nontrivial modification of HSIC and dCov (called xHSIC and xdCov, pronounced ``cross'' HSIC/dCov) so that they have a limiting Gaussian distribution under the null, and thus do not require permutations. This requires building on the newly developed theory of cross U-statistics by Kim and Ramdas (2020), and in particular developing several nontrivial extensions of the theory in Shekhar et al. (2022), which developed an analogous permutation-free kernel two-sample test. We show that our new tests, like the originals, are consistent against fixed alternatives, and minimax rate optimal against smooth local alternatives. Numerical simulations demonstrate that compared to the full dCov or HSIC, our variants have the same power up to a $\sqrt 2$ factor, giving practitioners a new option for large problems or data-analysis pipelines where computation, not sample size, could be the bottleneck.
A Permutation-free Kernel Two-Sample Test
Nov 27, 2022



Abstract:The kernel Maximum Mean Discrepancy~(MMD) is a popular multivariate distance metric between distributions that has found utility in two-sample testing. The usual kernel-MMD test statistic is a degenerate U-statistic under the null, and thus it has an intractable limiting distribution. Hence, to design a level-$\alpha$ test, one usually selects the rejection threshold as the $(1-\alpha)$-quantile of the permutation distribution. The resulting nonparametric test has finite-sample validity but suffers from large computational cost, since every permutation takes quadratic time. We propose the cross-MMD, a new quadratic-time MMD test statistic based on sample-splitting and studentization. We prove that under mild assumptions, the cross-MMD has a limiting standard Gaussian distribution under the null. Importantly, we also show that the resulting test is consistent against any fixed alternative, and when using the Gaussian kernel, it has minimax rate-optimal power against local alternatives. For large sample sizes, our new cross-MMD provides a significant speedup over the MMD, for only a slight loss in power.
Instance-Dependent Regret Analysis of Kernelized Bandits
Mar 12, 2022
Abstract:We study the kernelized bandit problem, that involves designing an adaptive strategy for querying a noisy zeroth-order-oracle to efficiently learn about the optimizer of an unknown function $f$ with a norm bounded by $M<\infty$ in a Reproducing Kernel Hilbert Space~(RKHS) associated with a positive definite kernel $K$. Prior results, working in a \emph{minimax framework}, have characterized the worst-case~(over all functions in the problem class) limits on regret achievable by \emph{any} algorithm, and have constructed algorithms with matching~(modulo polylogarithmic factors) worst-case performance for the \matern family of kernels. These results suffer from two drawbacks. First, the minimax lower bound gives no information about the limits of regret achievable by the commonly used algorithms on specific problem instances. Second, due to their worst-case nature, the existing upper bound analysis fails to adapt to easier problem instances within the function class. Our work takes steps to address both these issues. First, we derive \emph{instance-dependent} regret lower bounds for algorithms with uniformly~(over the function class) vanishing normalized cumulative regret. Our result, valid for all the practically relevant kernelized bandits algorithms, such as, GP-UCB, GP-TS and SupKernelUCB, identifies a fundamental complexity measure associated with every problem instance. We then address the second issue, by proposing a new minimax near-optimal algorithm which also adapts to easier problem instances.
Uncertainty-aware Safe Exploratory Planning using Gaussian Process and Neural Control Contraction Metric
May 13, 2021
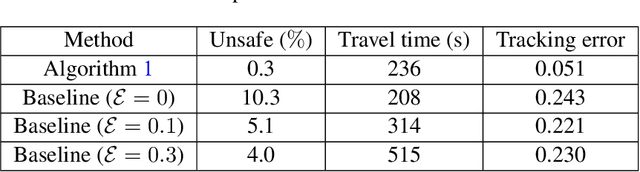
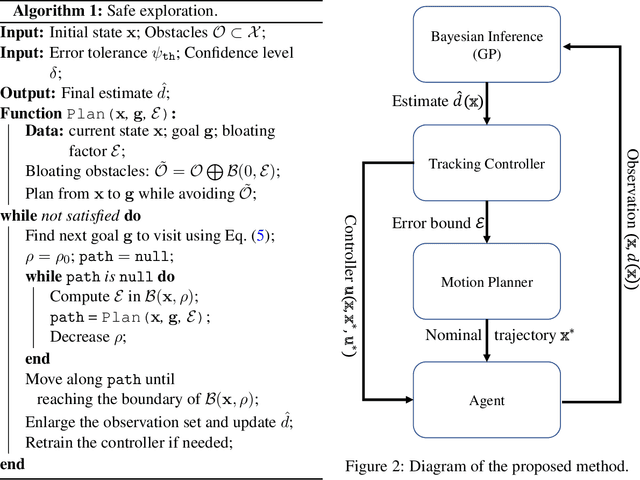

Abstract:In this paper, we consider the problem of using a robot to explore an environment with an unknown, state-dependent disturbance function while avoiding some forbidden areas. The goal of the robot is to safely collect observations of the disturbance and construct an accurate estimate of the underlying disturbance function. We use Gaussian Process (GP) to get an estimate of the disturbance from data with a high-confidence bound on the regression error. Furthermore, we use neural Contraction Metrics to derive a tracking controller and the corresponding high-confidence uncertainty tube around the nominal trajectory planned for the robot, based on the estimate of the disturbance. From the robustness of the Contraction Metric, error bound can be pre-computed and used by the motion planner such that the actual trajectory is guaranteed to be safe. As the robot collects more and more observations along its trajectory, the estimate of the disturbance becomes more and more accurate, which in turn improves the performance of the tracking controller and enlarges the free space that the robot can safely explore. We evaluate the proposed method using a carefully designed environment with a ground vehicle. Results show that with the proposed method the robot can thoroughly explore the environment safely and quickly.
Adaptive Sampling for Minimax Fair Classification
Mar 01, 2021



Abstract:Machine learning models trained on imbalanced datasets can often end up adversely affecting inputs belonging to the underrepresented groups. To address this issue, we consider the problem of adaptively constructing training sets which allow us to learn classifiers that are fair in a minimax sense. We first propose an adaptive sampling algorithm based on the principle of optimism, and derive theoretical bounds on its performance. We then suitably adapt the techniques developed for the analysis of our proposed algorithm to derive bounds on the performance of a related $\epsilon$-greedy strategy recently proposed in the literature. Next, by deriving algorithm independent lower-bounds for a specific class of problems, we show that the performance achieved by our adaptive scheme cannot be improved in general. We then validate the benefits of adaptively constructing training sets via experiments on synthetic tasks with logistic regression classifiers, as well as on several real-world tasks using convolutional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge