Modeling Human Beliefs about AI Behavior for Scalable Oversight

Contemporary work in AI alignment often relies on human feedback to teach AI systems human preferences and values. Yet as AI systems grow more capable, human feedback becomes increasingly unreliable. This raises the problem of scalable oversight: How can we supervise AI systems that exceed human capabilities? In this work, we propose to model the human evaluator's beliefs about the AI system's behavior to better interpret the human's feedback. We formalize human belief models and theoretically analyze their role in inferring human values. We then characterize the remaining ambiguity in this inference and conditions for which the ambiguity disappears. To mitigate reliance on exact belief models, we then introduce the relaxation of human belief model covering. Finally, we propose using foundation models to construct covering belief models, providing a new potential approach to scalable oversight.

Nonparametric Bayesian networks are typically faithful in the total variation metric

We show that for a given DAG $G$, among all observational distributions of Bayesian networks over $G$ with arbitrary outcome spaces, the faithful distributions are `typical': they constitute a dense, open set with respect to the total variation metric. As a consequence, the set of faithful distributions is non-empty, and the unfaithful distributions are nowhere dense. We extend this result to the space of Bayesian networks, where the properties hold for Bayesian networks instead of distributions of Bayesian networks. As special cases, we show that these results also hold for the faithful parameters of the subclasses of linear Gaussian -- and discrete Bayesian networks, giving a topological analogue of the measure-zero results of Spirtes et al. (1993) and Meek (1995). Finally, we extend our topological results and the measure-zero results of Spirtes et al. and Meek to Bayesian networks with latent variables.

Robust Multi-view Co-expression Network Inference

Unraveling the co-expression of genes across studies enhances the understanding of cellular processes. Inferring gene co-expression networks from transcriptome data presents many challenges, including spurious gene correlations, sample correlations, and batch effects. To address these complexities, we introduce a robust method for high-dimensional graph inference from multiple independent studies. We base our approach on the premise that each dataset is essentially a noisy linear mixture of gene loadings that follow a multivariate $t$-distribution with a sparse precision matrix, which is shared across studies. This allows us to show that we can identify the co-expression matrix up to a scaling factor among other model parameters. Our method employs an Expectation-Maximization procedure for parameter estimation. Empirical evaluation on synthetic and gene expression data demonstrates our method's improved ability to learn the underlying graph structure compared to baseline methods.

Towards detailed and interpretable hybrid modeling of continental-scale bird migration

Hybrid modeling aims to augment traditional theory-driven models with machine learning components that learn unknown parameters, sub-models or correction terms from data. In this work, we build on FluxRGNN, a recently developed hybrid model of continental-scale bird migration, which combines a movement model inspired by fluid dynamics with recurrent neural networks that capture the complex decision-making processes of birds. While FluxRGNN has been shown to successfully predict key migration patterns, its spatial resolution is constrained by the typically sparse observations obtained from weather radars. Additionally, its trainable components lack explicit incentives to adequately predict take-off and landing events. Both aspects limit our ability to interpret model results ecologically. To address this, we propose two major modifications that allow for more detailed predictions on any desired tessellation while providing control over the interpretability of model components. In experiments on the U.S. weather radar network, the enhanced model effectively leverages the underlying movement model, resulting in strong extrapolation capabilities to unobserved locations.

The Perils of Optimizing Learned Reward Functions: Low Training Error Does Not Guarantee Low Regret

In reinforcement learning, specifying reward functions that capture the intended task can be very challenging. Reward learning aims to address this issue by learning the reward function. However, a learned reward model may have a low error on the training distribution, and yet subsequently produce a policy with large regret. We say that such a reward model has an error-regret mismatch. The main source of an error-regret mismatch is the distributional shift that commonly occurs during policy optimization. In this paper, we mathematically show that a sufficiently low expected test error of the reward model guarantees low worst-case regret, but that for any fixed expected test error, there exist realistic data distributions that allow for error-regret mismatch to occur. We then show that similar problems persist even when using policy regularization techniques, commonly employed in methods such as RLHF. Our theoretical results highlight the importance of developing new ways to measure the quality of learned reward models.

Multivector Neurons: Better and Faster O(n)-Equivariant Clifford Graph Neural Networks

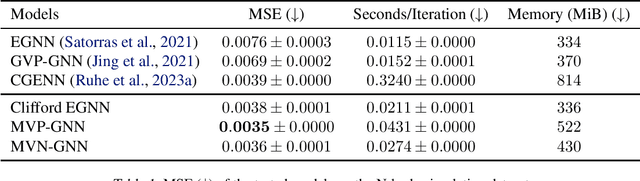
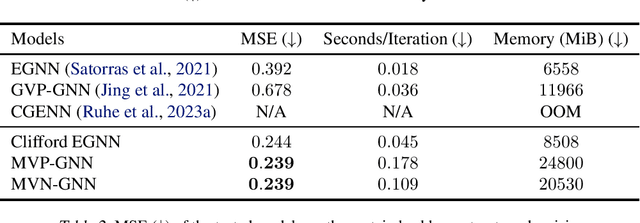
Most current deep learning models equivariant to $O(n)$ or $SO(n)$ either consider mostly scalar information such as distances and angles or have a very high computational complexity. In this work, we test a few novel message passing graph neural networks (GNNs) based on Clifford multivectors, structured similarly to other prevalent equivariant models in geometric deep learning. Our approach leverages efficient invariant scalar features while simultaneously performing expressive learning on multivector representations, particularly through the use of the equivariant geometric product operator. By integrating these elements, our methods outperform established efficient baseline models on an N-Body simulation task and protein denoising task while maintaining a high efficiency. In particular, we push the state-of-the-art error on the N-body dataset to 0.0035 (averaged over 3 runs); an 8% improvement over recent methods. Our implementation is available on Github.

Clifford-Steerable Convolutional Neural Networks

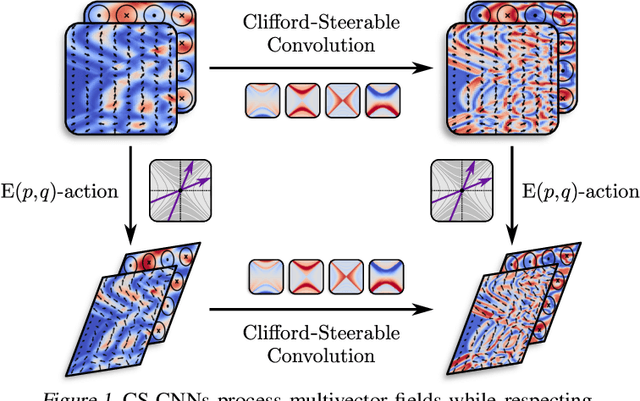
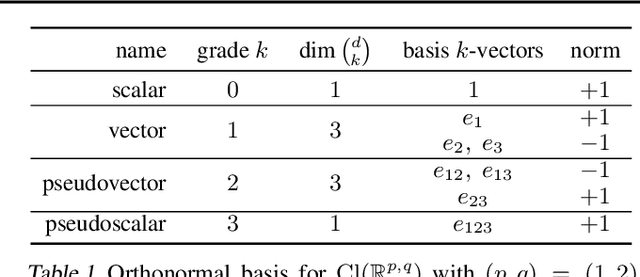
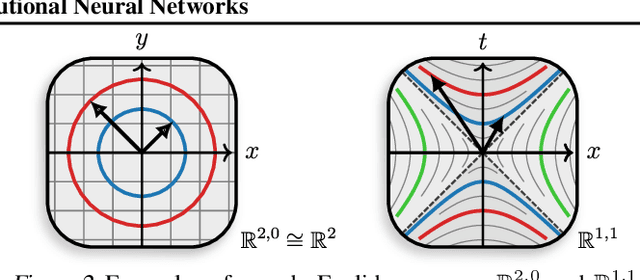
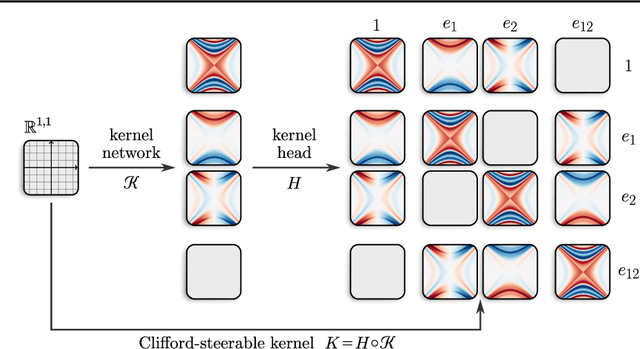
We present Clifford-Steerable Convolutional Neural Networks (CS-CNNs), a novel class of $\mathrm{E}(p, q)$-equivariant CNNs. CS-CNNs process multivector fields on pseudo-Euclidean spaces $\mathbb{R}^{p,q}$. They cover, for instance, $\mathrm{E}(3)$-equivariance on $\mathbb{R}^3$ and Poincar\'e-equivariance on Minkowski spacetime $\mathbb{R}^{1,3}$. Our approach is based on an implicit parametrization of $\mathrm{O}(p,q)$-steerable kernels via Clifford group equivariant neural networks. We significantly and consistently outperform baseline methods on fluid dynamics as well as relativistic electrodynamics forecasting tasks.

Clifford Group Equivariant Simplicial Message Passing Networks

We introduce Clifford Group Equivariant Simplicial Message Passing Networks, a method for steerable E(n)-equivariant message passing on simplicial complexes. Our method integrates the expressivity of Clifford group-equivariant layers with simplicial message passing, which is topologically more intricate than regular graph message passing. Clifford algebras include higher-order objects such as bivectors and trivectors, which express geometric features (e.g., areas, volumes) derived from vectors. Using this knowledge, we represent simplex features through geometric products of their vertices. To achieve efficient simplicial message passing, we share the parameters of the message network across different dimensions. Additionally, we restrict the final message to an aggregation of the incoming messages from different dimensions, leading to what we term shared simplicial message passing. Experimental results show that our method is able to outperform both equivariant and simplicial graph neural networks on a variety of geometric tasks.

Designing Long-term Group Fair Policies in Dynamical Systems

Neglecting the effect that decisions have on individuals (and thus, on the underlying data distribution) when designing algorithmic decision-making policies may increase inequalities and unfairness in the long term - even if fairness considerations were taken in the policy design process. In this paper, we propose a novel framework for achieving long-term group fairness in dynamical systems, in which current decisions may affect an individual's features in the next step, and thus, future decisions. Specifically, our framework allows us to identify a time-independent policy that converges, if deployed, to the targeted fair stationary state of the system in the long term, independently of the initial data distribution. We model the system dynamics with a time-homogeneous Markov chain and optimize the policy leveraging the Markov chain convergence theorem to ensure unique convergence. We provide examples of different targeted fair states of the system, encompassing a range of long-term goals for society and policymakers. Furthermore, we show how our approach facilitates the evaluation of different long-term targets by examining their impact on the group-conditional population distribution in the long term and how it evolves until convergence.

Anytime-Valid Confidence Sequences for Consistent Uncertainty Estimation in Early-Exit Neural Networks

Early-exit neural networks (EENNs) facilitate adaptive inference by producing predictions at multiple stages of the forward pass. In safety-critical applications, these predictions are only meaningful when complemented with reliable uncertainty estimates. Yet, due to their sequential structure, an EENN's uncertainty estimates should also be consistent: labels that are deemed improbable at one exit should not reappear within the confidence interval / set of later exits. We show that standard uncertainty quantification techniques, like Bayesian methods or conformal prediction, can lead to inconsistency across exits. We address this problem by applying anytime-valid confidence sequences (AVCSs) to the exits of EENNs. By design, AVCSs maintain consistency across exits. We examine the theoretical and practical challenges of applying AVCSs to EENNs and empirically validate our approach on both regression and classification tasks.