Equivariant non-linear maps for neural networks on homogeneous spaces

This paper presents a novel framework for non-linear equivariant neural network layers on homogeneous spaces. The seminal work of Cohen et al. on equivariant $G$-CNNs on homogeneous spaces characterized the representation theory of such layers in the linear setting, finding that they are given by convolutions with kernels satisfying so-called steerability constraints. Motivated by the empirical success of non-linear layers, such as self-attention or input dependent kernels, we set out to generalize these insights to the non-linear setting. We derive generalized steerability constraints that any such layer needs to satisfy and prove the universality of our construction. The insights gained into the symmetry-constrained functional dependence of equivariant operators on feature maps and group elements informs the design of future equivariant neural network layers. We demonstrate how several common equivariant network architectures - $G$-CNNs, implicit steerable kernel networks, conventional and relative position embedded attention based transformers, and LieTransformers - may be derived from our framework.

Clifford-Steerable Convolutional Neural Networks

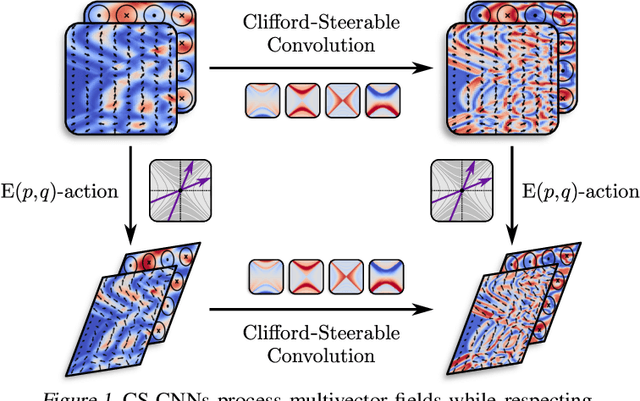
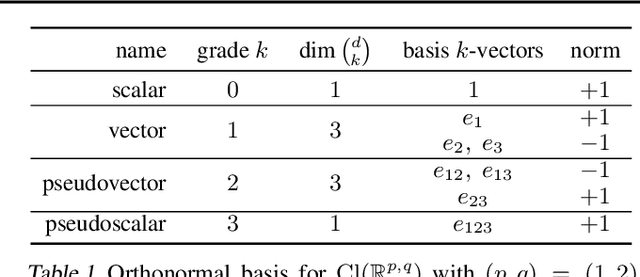
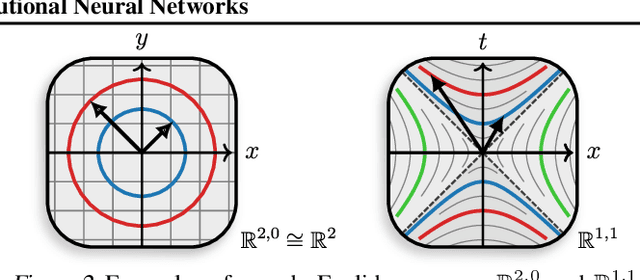
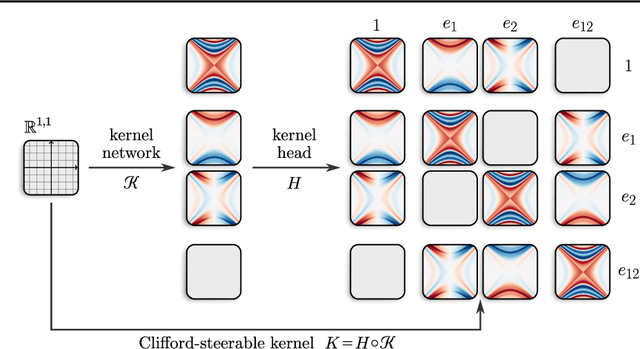
We present Clifford-Steerable Convolutional Neural Networks (CS-CNNs), a novel class of $\mathrm{E}(p, q)$-equivariant CNNs. CS-CNNs process multivector fields on pseudo-Euclidean spaces $\mathbb{R}^{p,q}$. They cover, for instance, $\mathrm{E}(3)$-equivariance on $\mathbb{R}^3$ and Poincar\'e-equivariance on Minkowski spacetime $\mathbb{R}^{1,3}$. Our approach is based on an implicit parametrization of $\mathrm{O}(p,q)$-steerable kernels via Clifford group equivariant neural networks. We significantly and consistently outperform baseline methods on fluid dynamics as well as relativistic electrodynamics forecasting tasks.

Hyperbolic Convolutional Neural Networks

Deep Learning is mostly responsible for the surge of interest in Artificial Intelligence in the last decade. So far, deep learning researchers have been particularly successful in the domain of image processing, where Convolutional Neural Networks are used. Although excelling at image classification, Convolutional Neural Networks are quite naive in that no inductive bias is set on the embedding space for images. Similar flaws are also exhibited by another type of Convolutional Networks - Graph Convolutional Neural Networks. However, using non-Euclidean space for embedding data might result in more robust and explainable models. One example of such a non-Euclidean space is hyperbolic space. Hyperbolic spaces are particularly useful due to their ability to fit more data in a low-dimensional space and tree-likeliness properties. These attractive properties have been previously used in multiple papers which indicated that they are beneficial for building hierarchical embeddings using shallow models and, recently, using MLPs and RNNs. However, no papers have yet suggested a general approach to using Hyperbolic Convolutional Neural Networks for structured data processing, although these are the most common examples of data used. Therefore, the goal of this work is to devise a general recipe for building Hyperbolic Convolutional Neural Networks. We hypothesize that ability of hyperbolic space to capture hierarchy in the data would lead to better performance. This ability should be particularly useful in cases where data has a tree-like structure. Since this is the case for many existing datasets \citep{wordnet, imagenet, fb15k}, we argue that such a model would be advantageous both in terms of applications and future research prospects.

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

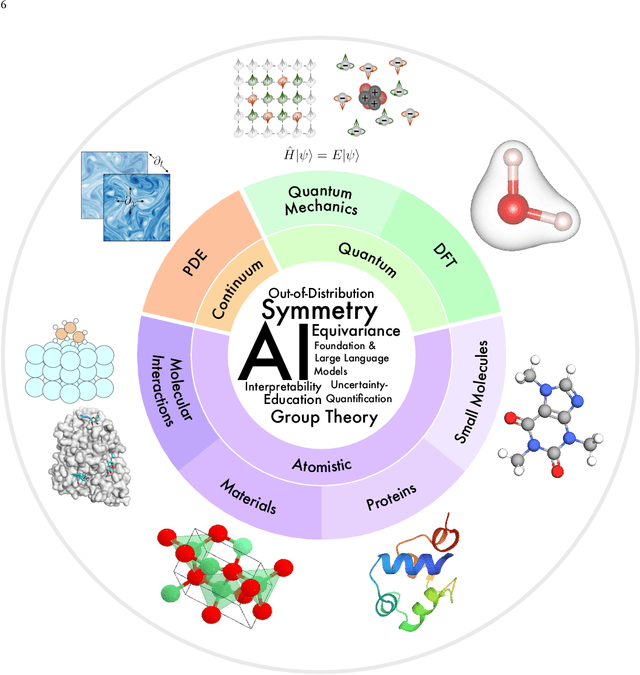
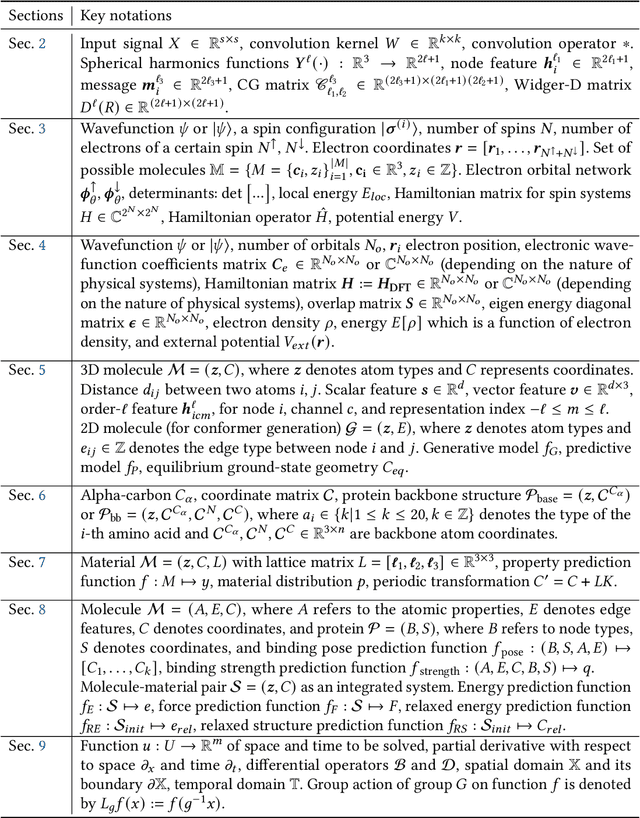
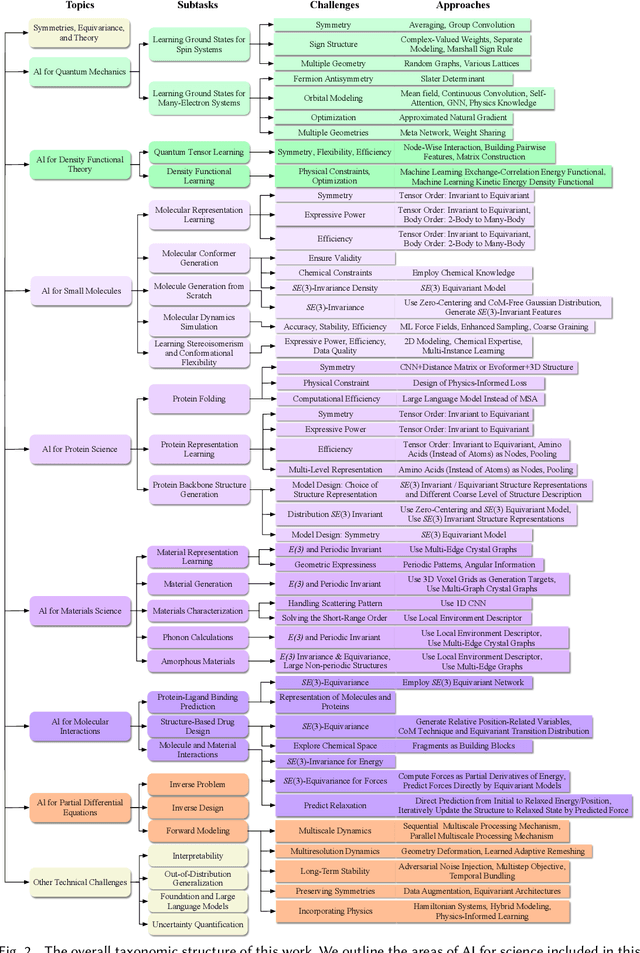
Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

Steerable Partial Differential Operators for Equivariant Neural Networks

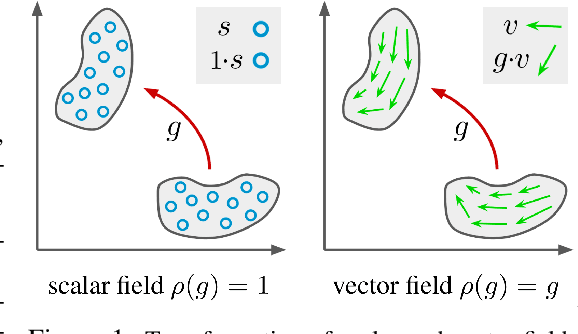
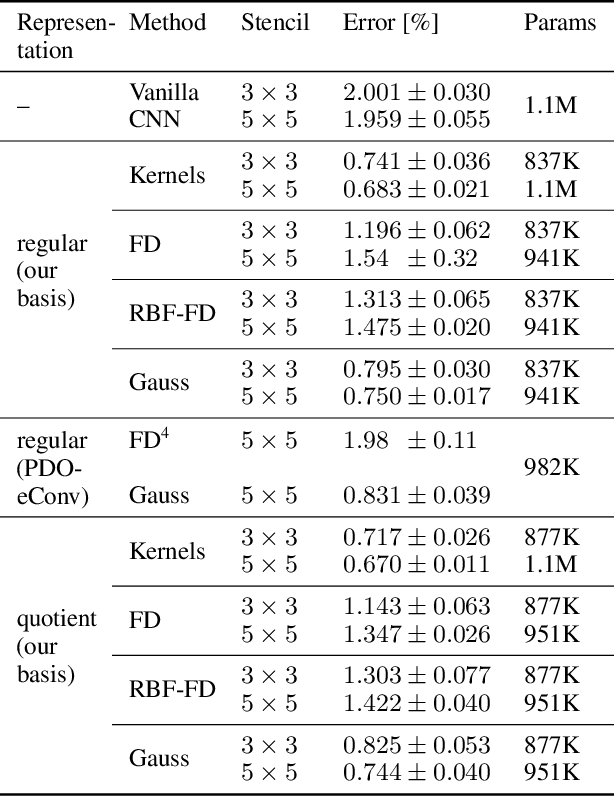
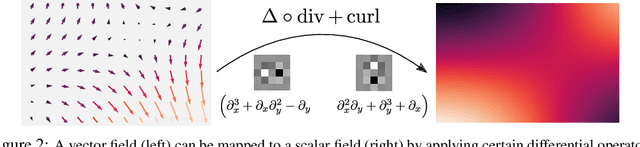
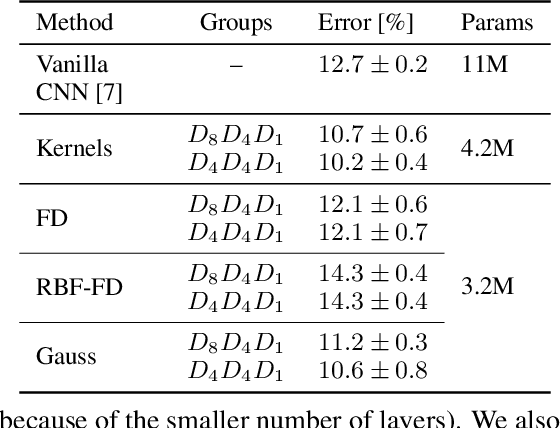
Recent work in equivariant deep learning bears strong similarities to physics. Fields over a base space are fundamental entities in both subjects, as are equivariant maps between these fields. In deep learning, however, these maps are usually defined by convolutions with a kernel, whereas they are partial differential operators (PDOs) in physics. Developing the theory of equivariant PDOs in the context of deep learning could bring these subjects even closer together and lead to a stronger flow of ideas. In this work, we derive a $G$-steerability constraint that completely characterizes when a PDO between feature vector fields is equivariant, for arbitrary symmetry groups $G$. We then fully solve this constraint for several important groups. We use our solutions as equivariant drop-in replacements for convolutional layers and benchmark them in that role. Finally, we develop a framework for equivariant maps based on Schwartz distributions that unifies classical convolutions and differential operators and gives insight about the relation between the two.

Coordinate Independent Convolutional Networks -- Isometry and Gauge Equivariant Convolutions on Riemannian Manifolds

Motivated by the vast success of deep convolutional networks, there is a great interest in generalizing convolutions to non-Euclidean manifolds. A major complication in comparison to flat spaces is that it is unclear in which alignment a convolution kernel should be applied on a manifold. The underlying reason for this ambiguity is that general manifolds do not come with a canonical choice of reference frames (gauge). Kernels and features therefore have to be expressed relative to arbitrary coordinates. We argue that the particular choice of coordinatization should not affect a network's inference -- it should be coordinate independent. A simultaneous demand for coordinate independence and weight sharing is shown to result in a requirement on the network to be equivariant under local gauge transformations (changes of local reference frames). The ambiguity of reference frames depends thereby on the G-structure of the manifold, such that the necessary level of gauge equivariance is prescribed by the corresponding structure group G. Coordinate independent convolutions are proven to be equivariant w.r.t. those isometries that are symmetries of the G-structure. The resulting theory is formulated in a coordinate free fashion in terms of fiber bundles. To exemplify the design of coordinate independent convolutions, we implement a convolutional network on the M\"obius strip. The generality of our differential geometric formulation of convolutional networks is demonstrated by an extensive literature review which explains a large number of Euclidean CNNs, spherical CNNs and CNNs on general surfaces as specific instances of coordinate independent convolutions.

A Wigner-Eckart Theorem for Group Equivariant Convolution Kernels

Group equivariant convolutional networks (GCNNs) endow classical convolutional networks with additional symmetry priors, which can lead to a considerably improved performance. Recent advances in the theoretical description of GCNNs revealed that such models can generally be understood as performing convolutions with G-steerable kernels, that is, kernels that satisfy an equivariance constraint themselves. While the G-steerability constraint has been derived, it has to date only been solved for specific use cases - a general characterization of G-steerable kernel spaces is still missing. This work provides such a characterization for the practically relevant case of G being any compact group. Our investigation is motivated by a striking analogy between the constraints underlying steerable kernels on the one hand and spherical tensor operators from quantum mechanics on the other hand. By generalizing the famous Wigner-Eckart theorem for spherical tensor operators, we prove that steerable kernel spaces are fully understood and parameterized in terms of 1) generalized reduced matrix elements, 2) Clebsch-Gordan coefficients, and 3) harmonic basis functions on homogeneous spaces.

Gauge Equivariant Mesh CNNs: Anisotropic convolutions on geometric graphs

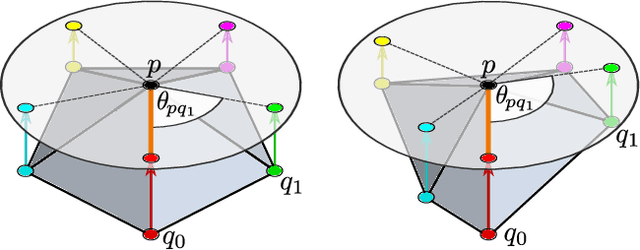
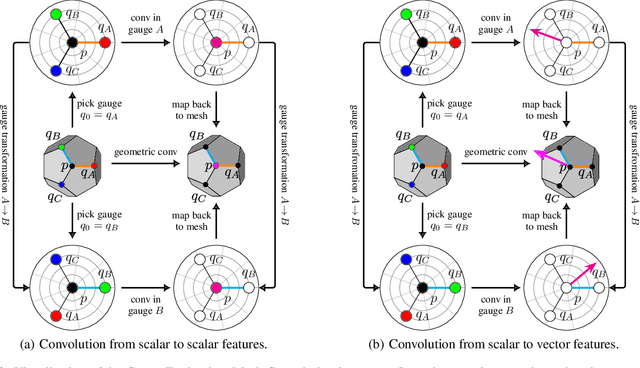
A common approach to define convolutions on meshes is to interpret them as a graph and apply graph convolutional networks (GCNs). Such GCNs utilize isotropic kernels and are therefore insensitive to the relative orientation of vertices and thus to the geometry of the mesh as a whole. We propose Gauge Equivariant Mesh CNNs which generalize GCNs to apply anisotropic gauge equivariant kernels. Since the resulting features carry orientation information, we introduce a geometric message passing scheme defined by parallel transporting features over mesh edges. Our experiments validate the significantly improved expressivity of the proposed model over conventional GCNs and other methods.

General $E(2)$-Equivariant Steerable CNNs

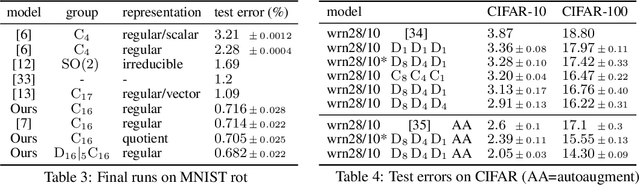
The big empirical success of group equivariant networks has led in recent years to the sprouting of a great variety of equivariant network architectures. A particular focus has thereby been on rotation and reflection equivariant CNNs for planar images. Here we give a general description of $E(2)$-equivariant convolutions in the framework of Steerable CNNs. The theory of Steerable CNNs thereby yields constraints on the convolution kernels which depend on group representations describing the transformation laws of feature spaces. We show that these constraints for arbitrary group representations can be reduced to constraints under irreducible representations. A general solution of the kernel space constraint is given for arbitrary representations of the Euclidean group $E(2)$ and its subgroups. We implement a wide range of previously proposed and entirely new equivariant network architectures and extensively compare their performances. $E(2)$-steerable convolutions are further shown to yield remarkable gains on CIFAR-10, CIFAR-100 and STL-10 when used as a drop-in replacement for non-equivariant convolutions.

Covariance in Physics and Convolutional Neural Networks

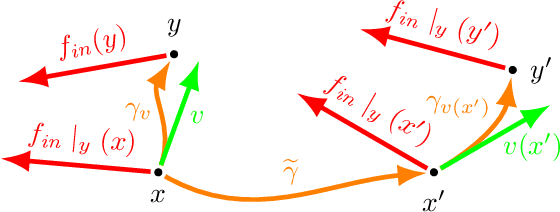
In this proceeding we give an overview of the idea of covariance (or equivariance) featured in the recent development of convolutional neural networks (CNNs). We study the similarities and differences between the use of covariance in theoretical physics and in the CNN context. Additionally, we demonstrate that the simple assumption of covariance, together with the required properties of locality, linearity and weight sharing, is sufficient to uniquely determine the form of the convolution.