Vassilis Anagiannis
Entangled q-Convolutional Neural Nets
Mar 06, 2021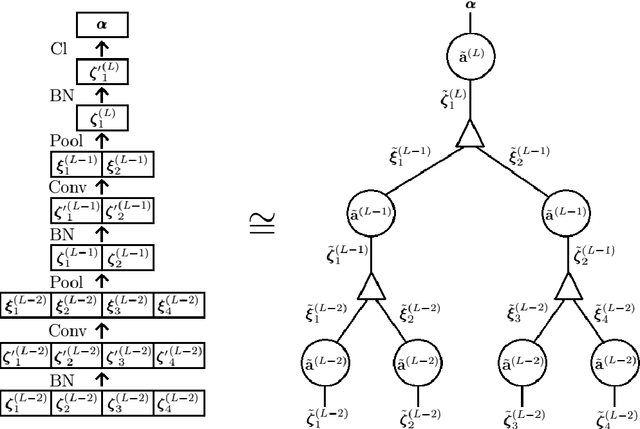
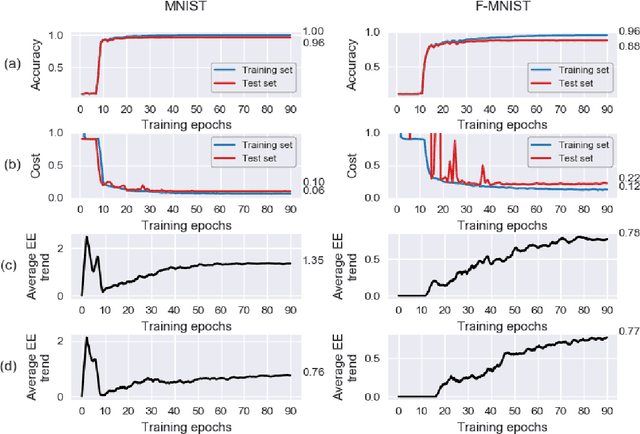
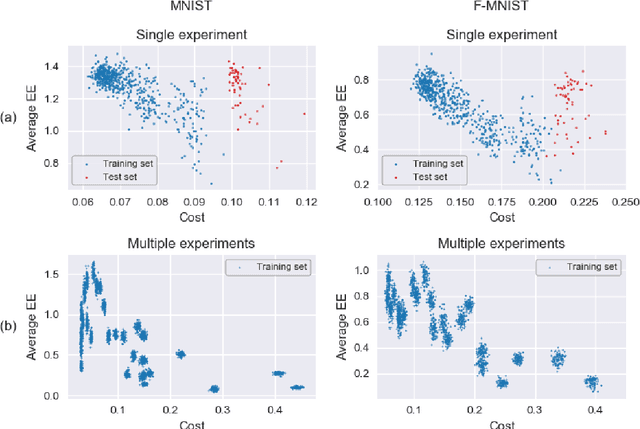
Abstract:We introduce a machine learning model, the q-CNN model, sharing key features with convolutional neural networks and admitting a tensor network description. As examples, we apply q-CNN to the MNIST and Fashion MNIST classification tasks. We explain how the network associates a quantum state to each classification label, and study the entanglement structure of these network states. In both our experiments on the MNIST and Fashion-MNIST datasets, we observe a distinct increase in both the left/right as well as the up/down bipartition entanglement entropy during training as the network learns the fine features of the data. More generally, we observe a universal negative correlation between the value of the entanglement entropy and the value of the cost function, suggesting that the network needs to learn the entanglement structure in order the perform the task accurately. This supports the possibility of exploiting the entanglement structure as a guide to design the machine learning algorithm suitable for given tasks.
Covariance in Physics and Convolutional Neural Networks
Jun 06, 2019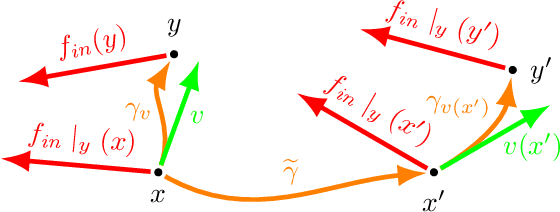
Abstract:In this proceeding we give an overview of the idea of covariance (or equivariance) featured in the recent development of convolutional neural networks (CNNs). We study the similarities and differences between the use of covariance in theoretical physics and in the CNN context. Additionally, we demonstrate that the simple assumption of covariance, together with the required properties of locality, linearity and weight sharing, is sufficient to uniquely determine the form of the convolution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge