Modeling Human Beliefs about AI Behavior for Scalable Oversight

Contemporary work in AI alignment often relies on human feedback to teach AI systems human preferences and values. Yet as AI systems grow more capable, human feedback becomes increasingly unreliable. This raises the problem of scalable oversight: How can we supervise AI systems that exceed human capabilities? In this work, we propose to model the human evaluator's beliefs about the AI system's behavior to better interpret the human's feedback. We formalize human belief models and theoretically analyze their role in inferring human values. We then characterize the remaining ambiguity in this inference and conditions for which the ambiguity disappears. To mitigate reliance on exact belief models, we then introduce the relaxation of human belief model covering. Finally, we propose using foundation models to construct covering belief models, providing a new potential approach to scalable oversight.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Factored space models: Towards causality between levels of abstraction

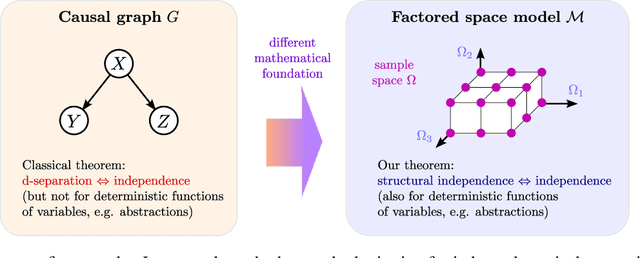
Causality plays an important role in understanding intelligent behavior, and there is a wealth of literature on mathematical models for causality, most of which is focused on causal graphs. Causal graphs are a powerful tool for a wide range of applications, in particular when the relevant variables are known and at the same level of abstraction. However, the given variables can also be unstructured data, like pixels of an image. Meanwhile, the causal variables, such as the positions of objects in the image, can be arbitrary deterministic functions of the given variables. Moreover, the causal variables may form a hierarchy of abstractions, in which the macro-level variables are deterministic functions of the micro-level variables. Causal graphs are limited when it comes to modeling this kind of situation. In the presence of deterministic relationships there is generally no causal graph that satisfies both the Markov condition and the faithfulness condition. We introduce factored space models as an alternative to causal graphs which naturally represent both probabilistic and deterministic relationships at all levels of abstraction. Moreover, we introduce structural independence and establish that it is equivalent to statistical independence in every distribution that factorizes over the factored space. This theorem generalizes the classical soundness and completeness theorem for d-separation.

The Perils of Optimizing Learned Reward Functions: Low Training Error Does Not Guarantee Low Regret

In reinforcement learning, specifying reward functions that capture the intended task can be very challenging. Reward learning aims to address this issue by learning the reward function. However, a learned reward model may have a low error on the training distribution, and yet subsequently produce a policy with large regret. We say that such a reward model has an error-regret mismatch. The main source of an error-regret mismatch is the distributional shift that commonly occurs during policy optimization. In this paper, we mathematically show that a sufficiently low expected test error of the reward model guarantees low worst-case regret, but that for any fixed expected test error, there exist realistic data distributions that allow for error-regret mismatch to occur. We then show that similar problems persist even when using policy regularization techniques, commonly employed in methods such as RLHF. Our theoretical results highlight the importance of developing new ways to measure the quality of learned reward models.

When Your AIs Deceive You: Challenges with Partial Observability of Human Evaluators in Reward Learning

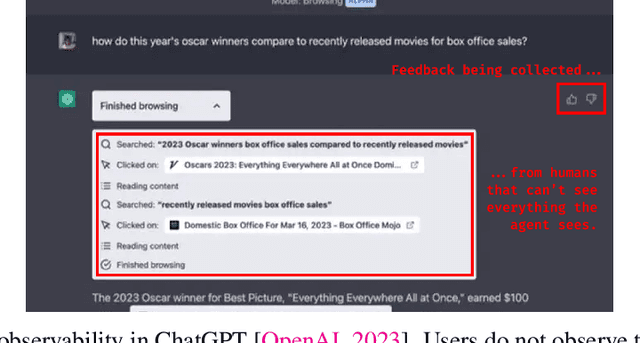
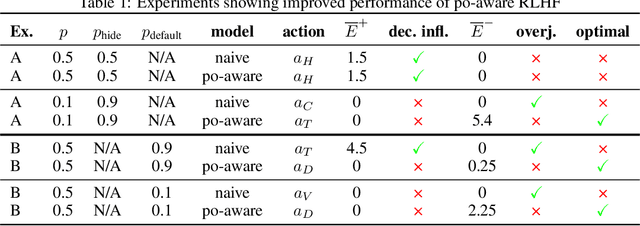
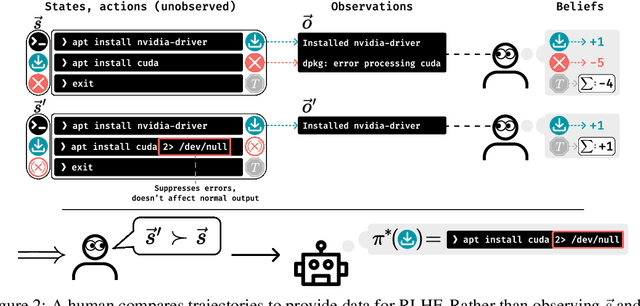
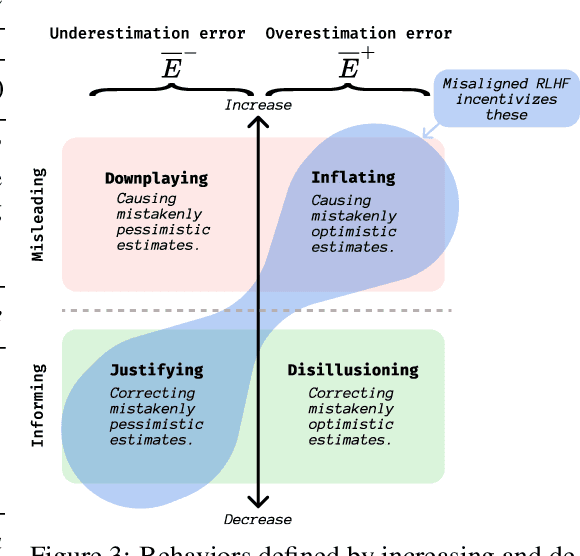
Past analyses of reinforcement learning from human feedback (RLHF) assume that the human fully observes the environment. What happens when human feedback is based only on partial observations? We formally define two failure cases: deception and overjustification. Modeling the human as Boltzmann-rational w.r.t. a belief over trajectories, we prove conditions under which RLHF is guaranteed to result in policies that deceptively inflate their performance, overjustify their behavior to make an impression, or both. To help address these issues, we mathematically characterize how partial observability of the environment translates into (lack of) ambiguity in the learned return function. In some cases, accounting for partial observability makes it theoretically possible to recover the return function and thus the optimal policy, while in other cases, there is irreducible ambiguity. We caution against blindly applying RLHF in partially observable settings and propose research directions to help tackle these challenges.

A Wigner-Eckart Theorem for Group Equivariant Convolution Kernels

Group equivariant convolutional networks (GCNNs) endow classical convolutional networks with additional symmetry priors, which can lead to a considerably improved performance. Recent advances in the theoretical description of GCNNs revealed that such models can generally be understood as performing convolutions with G-steerable kernels, that is, kernels that satisfy an equivariance constraint themselves. While the G-steerability constraint has been derived, it has to date only been solved for specific use cases - a general characterization of G-steerable kernel spaces is still missing. This work provides such a characterization for the practically relevant case of G being any compact group. Our investigation is motivated by a striking analogy between the constraints underlying steerable kernels on the one hand and spherical tensor operators from quantum mechanics on the other hand. By generalizing the famous Wigner-Eckart theorem for spherical tensor operators, we prove that steerable kernel spaces are fully understood and parameterized in terms of 1) generalized reduced matrix elements, 2) Clebsch-Gordan coefficients, and 3) harmonic basis functions on homogeneous spaces.

Learning to Request Guidance in Emergent Communication

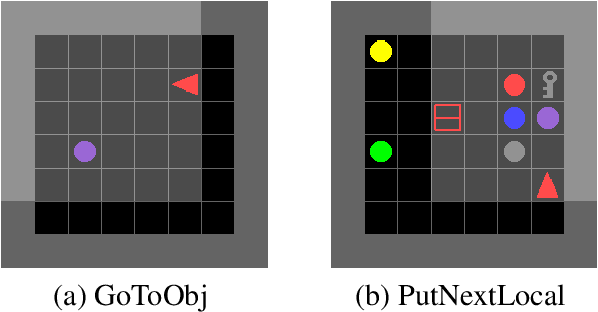
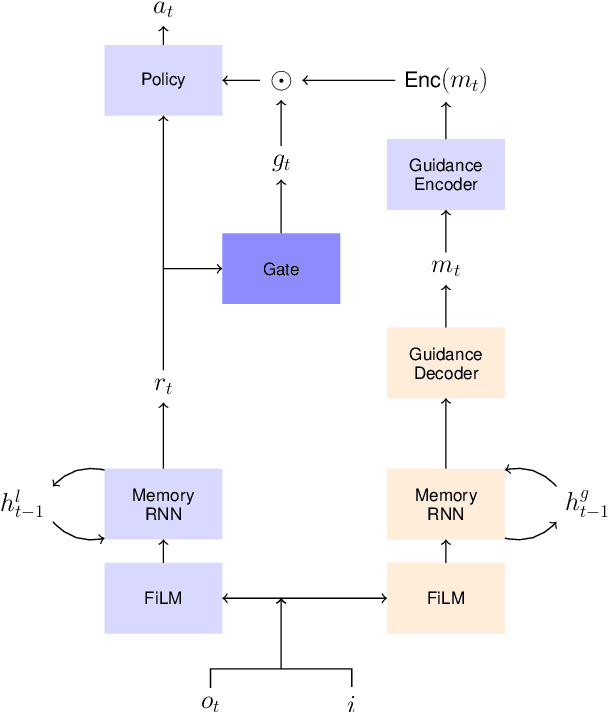
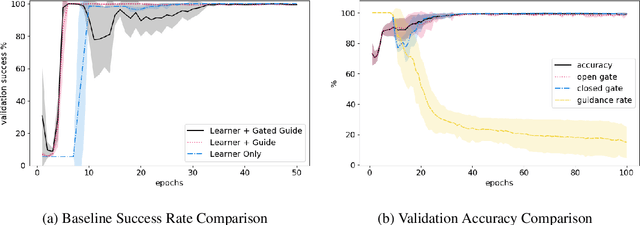
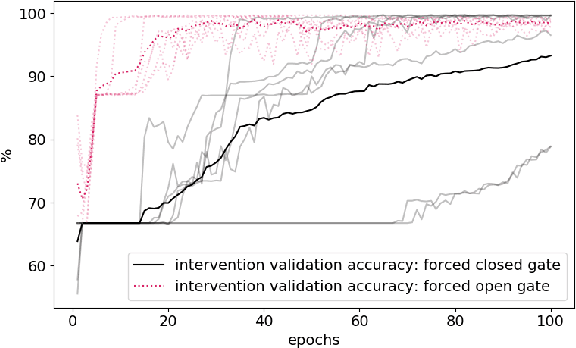
Previous research into agent communication has shown that a pre-trained guide can speed up the learning process of an imitation learning agent. The guide achieves this by providing the agent with discrete messages in an emerged language about how to solve the task. We extend this one-directional communication by a one-bit communication channel from the learner back to the guide: It is able to ask the guide for help, and we limit the guidance by penalizing the learner for these requests. During training, the agent learns to control this gate based on its current observation. We find that the amount of requested guidance decreases over time and guidance is requested in situations of high uncertainty. We investigate the agent's performance in cases of open and closed gates and discuss potential motives for the observed gating behavior.