David Speck
Symbolic Search for Optimal Planning with Expressive Extensions
Apr 01, 2022



Abstract:In classical planning, the goal is to derive a course of actions that allows an intelligent agent to move from any situation it finds itself in to one that satisfies its goals. Classical planning is considered domain-independent, i.e., it is not limited to a particular application and can be used to solve different types of reasoning problems. In practice, however, some properties of a planning problem at hand require an expressive extension of the standard classical planning formalism to capture and model them. Although the importance of many of these extensions is well known, most planners, especially optimal planners, do not support these extended planning formalisms. The lack of support not only limits the use of these planners for certain problems, but even if it is possible to model the problems without these extensions, it often leads to increased effort in modeling or makes modeling practically impossible as the required problem encoding size increases exponentially. In this thesis, we propose to use symbolic search for cost-optimal planning for different expressive extensions of classical planning, all capturing different aspects of the problem. In particular, we study planning with axioms, planning with state-dependent action costs, oversubscription planning, and top-k planning. For all formalisms, we present complexity and compilability results, highlighting that it is desirable and even necessary to natively support the corresponding features. We analyze symbolic heuristic search and show that the search performance does not always benefit from the use of a heuristic and that the search performance can exponentially deteriorate even under the best possible circumstances, namely the perfect heuristic. This reinforces that symbolic blind search is the dominant symbolic search strategy nowadays, on par with other state-of-the-art cost-optimal planning strategies...
Learning Heuristic Selection with Dynamic Algorithm Configuration
Jun 15, 2020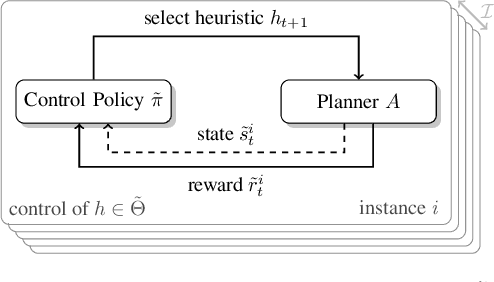

Abstract:A key challenge in satisfying planning is to use multiple heuristics within one heuristic search. An aggregation of multiple heuristic estimates, for example by taking the maximum, has the disadvantage that bad estimates of a single heuristic can negatively affect the whole search. Since the performance of a heuristic varies from instance to instance, approaches such as algorithm selection can be successfully applied. In addition, alternating between multiple heuristics during the search makes it possible to use all heuristics equally and improve performance. However, all these approaches ignore the internal search dynamics of a planning system, which can help to select the most helpful heuristics for the current expansion step. We show that dynamic algorithm configuration can be used for dynamic heuristic selection which takes into account the internal search dynamics of a planning system. Furthermore, we prove that this approach generalizes over existing approaches and that it can exponentially improve the performance of the heuristic search. To learn dynamic heuristic selection, we propose an approach based on reinforcement learning and show empirically that domain-wise learned policies, which take the internal search dynamics of a planning system into account, can exceed existing approaches in terms of coverage.
Learning to Request Guidance in Emergent Communication
Dec 11, 2019
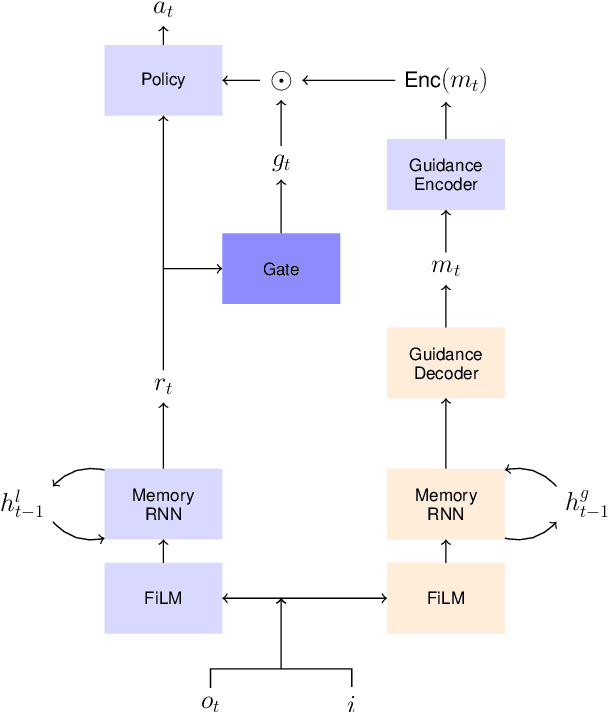
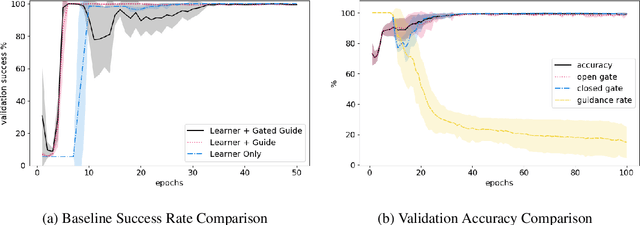
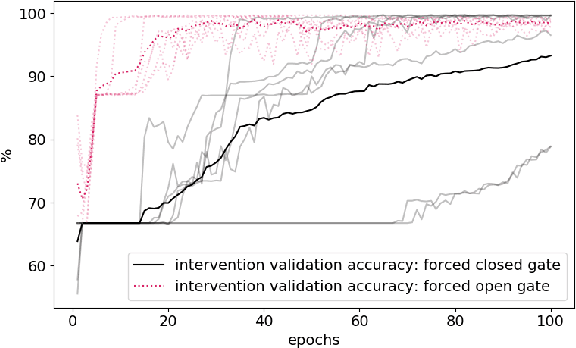
Abstract:Previous research into agent communication has shown that a pre-trained guide can speed up the learning process of an imitation learning agent. The guide achieves this by providing the agent with discrete messages in an emerged language about how to solve the task. We extend this one-directional communication by a one-bit communication channel from the learner back to the guide: It is able to ask the guide for help, and we limit the guidance by penalizing the learner for these requests. During training, the agent learns to control this gate based on its current observation. We find that the amount of requested guidance decreases over time and guidance is requested in situations of high uncertainty. We investigate the agent's performance in cases of open and closed gates and discuss potential motives for the observed gating behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge