Factored space models: Towards causality between levels of abstraction

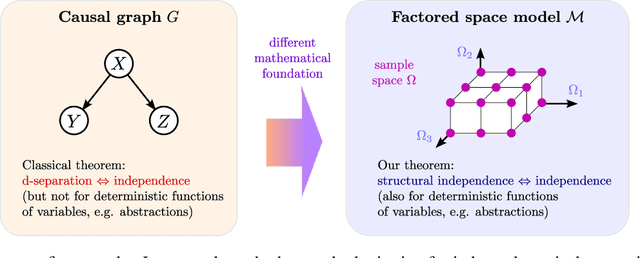
Causality plays an important role in understanding intelligent behavior, and there is a wealth of literature on mathematical models for causality, most of which is focused on causal graphs. Causal graphs are a powerful tool for a wide range of applications, in particular when the relevant variables are known and at the same level of abstraction. However, the given variables can also be unstructured data, like pixels of an image. Meanwhile, the causal variables, such as the positions of objects in the image, can be arbitrary deterministic functions of the given variables. Moreover, the causal variables may form a hierarchy of abstractions, in which the macro-level variables are deterministic functions of the micro-level variables. Causal graphs are limited when it comes to modeling this kind of situation. In the presence of deterministic relationships there is generally no causal graph that satisfies both the Markov condition and the faithfulness condition. We introduce factored space models as an alternative to causal graphs which naturally represent both probabilistic and deterministic relationships at all levels of abstraction. Moreover, we introduce structural independence and establish that it is equivalent to statistical independence in every distribution that factorizes over the factored space. This theorem generalizes the classical soundness and completeness theorem for d-separation.

Temporal Inference with Finite Factored Sets

We propose a new approach to temporal inference, inspired by the Pearlian causal inference paradigm - though quite different from Pearl's approach formally. Rather than using directed acyclic graphs, we make use of factored sets, which are sets expressed as Cartesian products. We show that finite factored sets are powerful tools for inferring temporal relations. We introduce an analog of d-separation for factored sets, conditional orthogonality, and we demonstrate that this notion is equivalent to conditional independence in all probability distributions on a finite factored set.

Risks from Learned Optimization in Advanced Machine Learning Systems

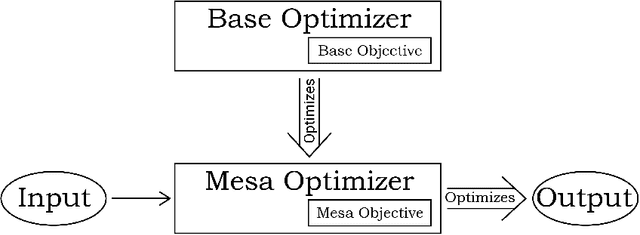
We analyze the type of learned optimization that occurs when a learned model (such as a neural network) is itself an optimizer - a situation we refer to as mesa-optimization, a neologism we introduce in this paper. We believe that the possibility of mesa-optimization raises two important questions for the safety and transparency of advanced machine learning systems. First, under what circumstances will learned models be optimizers, including when they should not be? Second, when a learned model is an optimizer, what will its objective be - how will it differ from the loss function it was trained under - and how can it be aligned? In this paper, we provide an in-depth analysis of these two primary questions and provide an overview of topics for future research.

Embedded Agency

Traditional models of rational action treat the agent as though it is cleanly separated from its environment, and can act on that environment from the outside. Such agents have a known functional relationship with their environment, can model their environment in every detail, and do not need to reason about themselves or their internal parts. We provide an informal survey of obstacles to formalizing good reasoning for agents embedded in their environment. Such agents must optimize an environment that is not of type ``function''; they must rely on models that fit within the modeled environment; and they must reason about themselves as just another physical system, made of parts that can be modified and that can work at cross purposes.

Categorizing Variants of Goodhart's Law

There are several distinct failure modes for overoptimization of systems on the basis of metrics. This occurs when a metric which can be used to improve a system is used to an extent that further optimization is ineffective or harmful, and is sometimes termed Goodhart's Law. This class of failure is often poorly understood, partly because terminology for discussing them is ambiguous, and partly because discussion using this ambiguous terminology ignores distinctions between different failure modes of this general type. This paper expands on an earlier discussion by Garrabrant, which notes there are "(at least) four different mechanisms" that relate to Goodhart's Law. This paper is intended to explore these mechanisms further, and specify more clearly how they occur. This discussion should be helpful in better understanding these types of failures in economic regulation, in public policy, in machine learning, and in Artificial Intelligence alignment. The importance of Goodhart effects depends on the amount of power directed towards optimizing the proxy, and so the increased optimization power offered by artificial intelligence makes it especially critical for that field.

Logical Induction

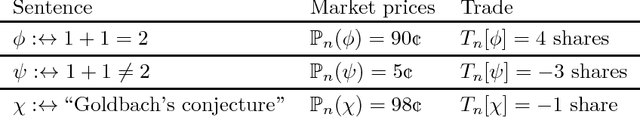
We present a computable algorithm that assigns probabilities to every logical statement in a given formal language, and refines those probabilities over time. For instance, if the language is Peano arithmetic, it assigns probabilities to all arithmetical statements, including claims about the twin prime conjecture, the outputs of long-running computations, and its own probabilities. We show that our algorithm, an instance of what we call a logical inductor, satisfies a number of intuitive desiderata, including: (1) it learns to predict patterns of truth and falsehood in logical statements, often long before having the resources to evaluate the statements, so long as the patterns can be written down in polynomial time; (2) it learns to use appropriate statistical summaries to predict sequences of statements whose truth values appear pseudorandom; and (3) it learns to have accurate beliefs about its own current beliefs, in a manner that avoids the standard paradoxes of self-reference. For example, if a given computer program only ever produces outputs in a certain range, a logical inductor learns this fact in a timely manner; and if late digits in the decimal expansion of $\pi$ are difficult to predict, then a logical inductor learns to assign $\approx 10\%$ probability to "the $n$th digit of $\pi$ is a 7" for large $n$. Logical inductors also learn to trust their future beliefs more than their current beliefs, and their beliefs are coherent in the limit (whenever $\phi \implies \psi$, $\mathbb{P}_\infty(\phi) \le \mathbb{P}_\infty(\psi)$, and so on); and logical inductors strictly dominate the universal semimeasure in the limit. These properties and many others all follow from a single logical induction criterion, which is motivated by a series of stock trading analogies. Roughly speaking, each logical sentence $\phi$ is associated with a stock that is worth \$1 per share if [...]

Inductive Coherence

While probability theory is normally applied to external environments, there has been some recent interest in probabilistic modeling of the outputs of computations that are too expensive to run. Since mathematical logic is a powerful tool for reasoning about computer programs, we consider this problem from the perspective of integrating probability and logic. Recent work on assigning probabilities to mathematical statements has used the concept of coherent distributions, which satisfy logical constraints such as the probability of a sentence and its negation summing to one. Although there are algorithms which converge to a coherent probability distribution in the limit, this yields only weak guarantees about finite approximations of these distributions. In our setting, this is a significant limitation: Coherent distributions assign probability one to all statements provable in a specific logical theory, such as Peano Arithmetic, which can prove what the output of any terminating computation is; thus, a coherent distribution must assign probability one to the output of any terminating computation. To model uncertainty about computations, we propose to work with approximations to coherent distributions. We introduce inductive coherence, a strengthening of coherence that provides appropriate constraints on finite approximations, and propose an algorithm which satisfies this criterion.

Asymptotic Convergence in Online Learning with Unbounded Delays

We study the problem of predicting the results of computations that are too expensive to run, via the observation of the results of smaller computations. We model this as an online learning problem with delayed feedback, where the length of the delay is unbounded, which we study mainly in a stochastic setting. We show that in this setting, consistency is not possible in general, and that optimal forecasters might not have average regret going to zero. However, it is still possible to give algorithms that converge asymptotically to Bayes-optimal predictions, by evaluating forecasters on specific sparse independent subsequences of their predictions. We give an algorithm that does this, which converges asymptotically on good behavior, and give very weak bounds on how long it takes to converge. We then relate our results back to the problem of predicting large computations in a deterministic setting.

Asymptotic Logical Uncertainty and The Benford Test

We give an algorithm A which assigns probabilities to logical sentences. For any simple infinite sequence of sentences whose truth-values appear indistinguishable from a biased coin that outputs "true" with probability p, we have that the sequence of probabilities that A assigns to these sentences converges to p.