Functional Decision Theory: A New Theory of Instrumental Rationality

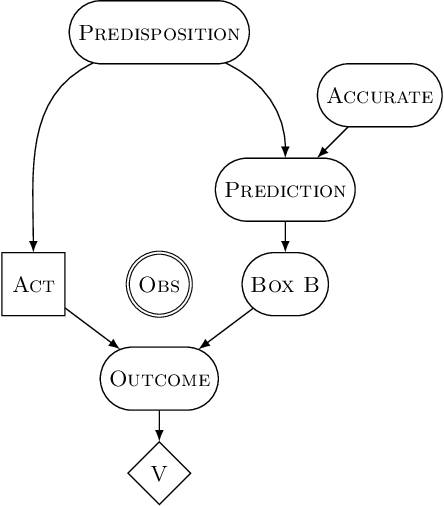
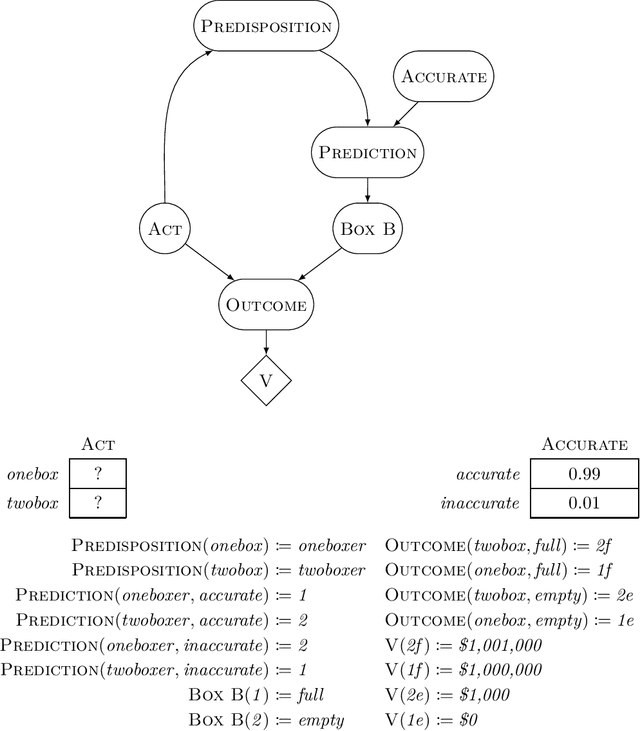
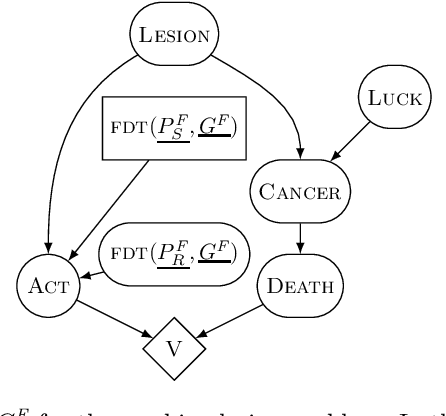
This paper describes and motivates a new decision theory known as functional decision theory (FDT), as distinct from causal decision theory and evidential decision theory. Functional decision theorists hold that the normative principle for action is to treat one's decision as the output of a fixed mathematical function that answers the question, "Which output of this very function would yield the best outcome?" Adhering to this principle delivers a number of benefits, including the ability to maximize wealth in an array of traditional decision-theoretic and game-theoretic problems where CDT and EDT perform poorly. Using one simple and coherent decision rule, functional decision theorists (for example) achieve more utility than CDT on Newcomb's problem, more utility than EDT on the smoking lesion problem, and more utility than both in Parfit's hitchhiker problem. In this paper, we define FDT, explore its prescriptions in a number of different decision problems, compare it to CDT and EDT, and give philosophical justifications for FDT as a normative theory of decision-making.

Logical Induction

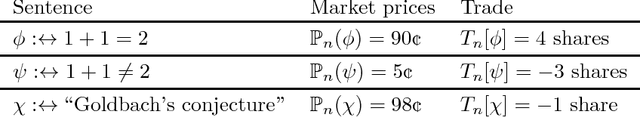
We present a computable algorithm that assigns probabilities to every logical statement in a given formal language, and refines those probabilities over time. For instance, if the language is Peano arithmetic, it assigns probabilities to all arithmetical statements, including claims about the twin prime conjecture, the outputs of long-running computations, and its own probabilities. We show that our algorithm, an instance of what we call a logical inductor, satisfies a number of intuitive desiderata, including: (1) it learns to predict patterns of truth and falsehood in logical statements, often long before having the resources to evaluate the statements, so long as the patterns can be written down in polynomial time; (2) it learns to use appropriate statistical summaries to predict sequences of statements whose truth values appear pseudorandom; and (3) it learns to have accurate beliefs about its own current beliefs, in a manner that avoids the standard paradoxes of self-reference. For example, if a given computer program only ever produces outputs in a certain range, a logical inductor learns this fact in a timely manner; and if late digits in the decimal expansion of $\pi$ are difficult to predict, then a logical inductor learns to assign $\approx 10\%$ probability to "the $n$th digit of $\pi$ is a 7" for large $n$. Logical inductors also learn to trust their future beliefs more than their current beliefs, and their beliefs are coherent in the limit (whenever $\phi \implies \psi$, $\mathbb{P}_\infty(\phi) \le \mathbb{P}_\infty(\psi)$, and so on); and logical inductors strictly dominate the universal semimeasure in the limit. These properties and many others all follow from a single logical induction criterion, which is motivated by a series of stock trading analogies. Roughly speaking, each logical sentence $\phi$ is associated with a stock that is worth \$1 per share if [...]

Inductive Coherence

While probability theory is normally applied to external environments, there has been some recent interest in probabilistic modeling of the outputs of computations that are too expensive to run. Since mathematical logic is a powerful tool for reasoning about computer programs, we consider this problem from the perspective of integrating probability and logic. Recent work on assigning probabilities to mathematical statements has used the concept of coherent distributions, which satisfy logical constraints such as the probability of a sentence and its negation summing to one. Although there are algorithms which converge to a coherent probability distribution in the limit, this yields only weak guarantees about finite approximations of these distributions. In our setting, this is a significant limitation: Coherent distributions assign probability one to all statements provable in a specific logical theory, such as Peano Arithmetic, which can prove what the output of any terminating computation is; thus, a coherent distribution must assign probability one to the output of any terminating computation. To model uncertainty about computations, we propose to work with approximations to coherent distributions. We introduce inductive coherence, a strengthening of coherence that provides appropriate constraints on finite approximations, and propose an algorithm which satisfies this criterion.

Asymptotic Convergence in Online Learning with Unbounded Delays

We study the problem of predicting the results of computations that are too expensive to run, via the observation of the results of smaller computations. We model this as an online learning problem with delayed feedback, where the length of the delay is unbounded, which we study mainly in a stochastic setting. We show that in this setting, consistency is not possible in general, and that optimal forecasters might not have average regret going to zero. However, it is still possible to give algorithms that converge asymptotically to Bayes-optimal predictions, by evaluating forecasters on specific sparse independent subsequences of their predictions. We give an algorithm that does this, which converges asymptotically on good behavior, and give very weak bounds on how long it takes to converge. We then relate our results back to the problem of predicting large computations in a deterministic setting.

Toward Idealized Decision Theory

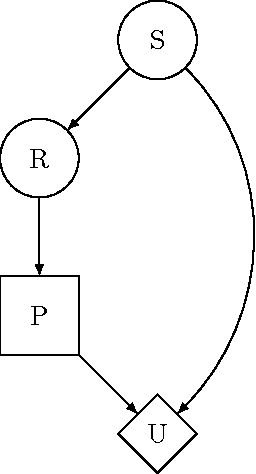
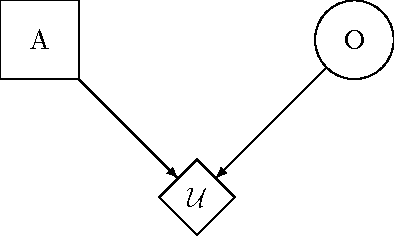
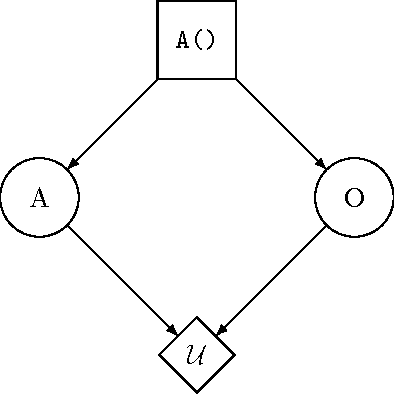
This paper motivates the study of decision theory as necessary for aligning smarter-than-human artificial systems with human interests. We discuss the shortcomings of two standard formulations of decision theory, and demonstrate that they cannot be used to describe an idealized decision procedure suitable for approximation by artificial systems. We then explore the notions of policy selection and logical counterfactuals, two recent insights into decision theory that point the way toward promising paths for future research.