Inductive Coherence

While probability theory is normally applied to external environments, there has been some recent interest in probabilistic modeling of the outputs of computations that are too expensive to run. Since mathematical logic is a powerful tool for reasoning about computer programs, we consider this problem from the perspective of integrating probability and logic. Recent work on assigning probabilities to mathematical statements has used the concept of coherent distributions, which satisfy logical constraints such as the probability of a sentence and its negation summing to one. Although there are algorithms which converge to a coherent probability distribution in the limit, this yields only weak guarantees about finite approximations of these distributions. In our setting, this is a significant limitation: Coherent distributions assign probability one to all statements provable in a specific logical theory, such as Peano Arithmetic, which can prove what the output of any terminating computation is; thus, a coherent distribution must assign probability one to the output of any terminating computation. To model uncertainty about computations, we propose to work with approximations to coherent distributions. We introduce inductive coherence, a strengthening of coherence that provides appropriate constraints on finite approximations, and propose an algorithm which satisfies this criterion.

A Formal Solution to the Grain of Truth Problem

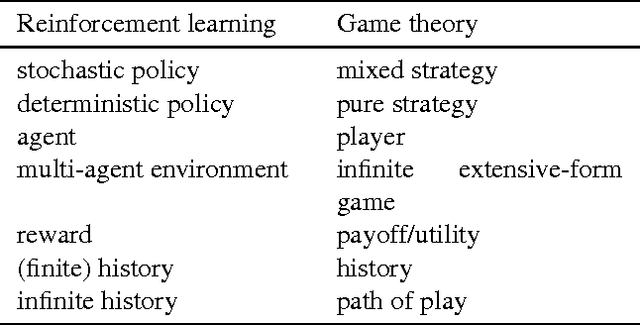
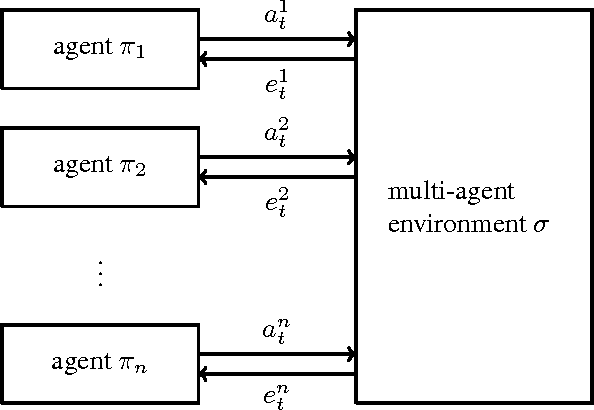
A Bayesian agent acting in a multi-agent environment learns to predict the other agents' policies if its prior assigns positive probability to them (in other words, its prior contains a \emph{grain of truth}). Finding a reasonably large class of policies that contains the Bayes-optimal policies with respect to this class is known as the \emph{grain of truth problem}. Only small classes are known to have a grain of truth and the literature contains several related impossibility results. In this paper we present a formal and general solution to the full grain of truth problem: we construct a class of policies that contains all computable policies as well as Bayes-optimal policies for every lower semicomputable prior over the class. When the environment is unknown, Bayes-optimal agents may fail to act optimally even asymptotically. However, agents based on Thompson sampling converge to play {\epsilon}-Nash equilibria in arbitrary unknown computable multi-agent environments. While these results are purely theoretical, we show that they can be computationally approximated arbitrarily closely.