A Formal Solution to the Grain of Truth Problem
Paper and Code
Sep 16, 2016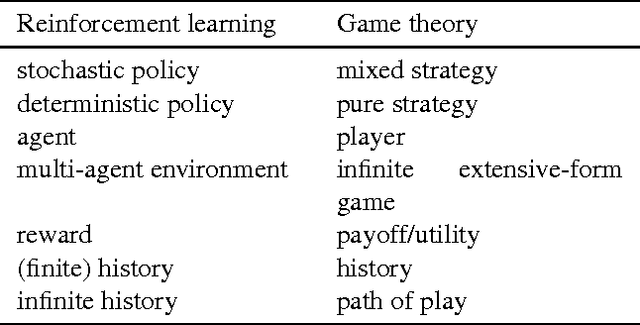

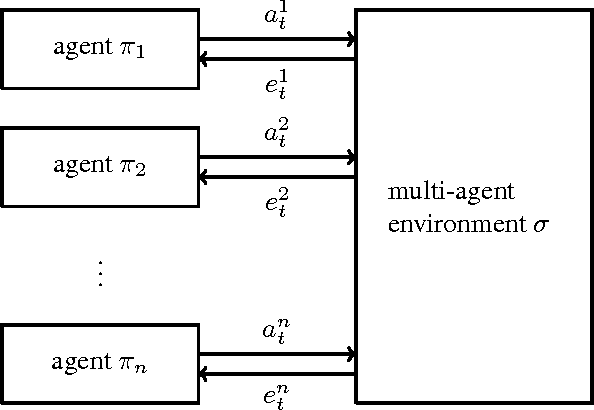
A Bayesian agent acting in a multi-agent environment learns to predict the other agents' policies if its prior assigns positive probability to them (in other words, its prior contains a \emph{grain of truth}). Finding a reasonably large class of policies that contains the Bayes-optimal policies with respect to this class is known as the \emph{grain of truth problem}. Only small classes are known to have a grain of truth and the literature contains several related impossibility results. In this paper we present a formal and general solution to the full grain of truth problem: we construct a class of policies that contains all computable policies as well as Bayes-optimal policies for every lower semicomputable prior over the class. When the environment is unknown, Bayes-optimal agents may fail to act optimally even asymptotically. However, agents based on Thompson sampling converge to play {\epsilon}-Nash equilibria in arbitrary unknown computable multi-agent environments. While these results are purely theoretical, we show that they can be computationally approximated arbitrarily closely.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge