Functional Decision Theory: A New Theory of Instrumental Rationality
Paper and Code
May 22, 2018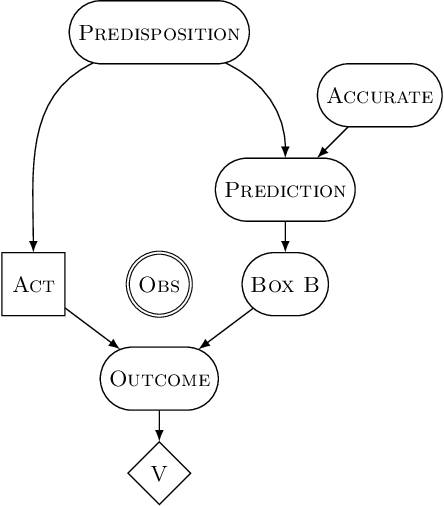
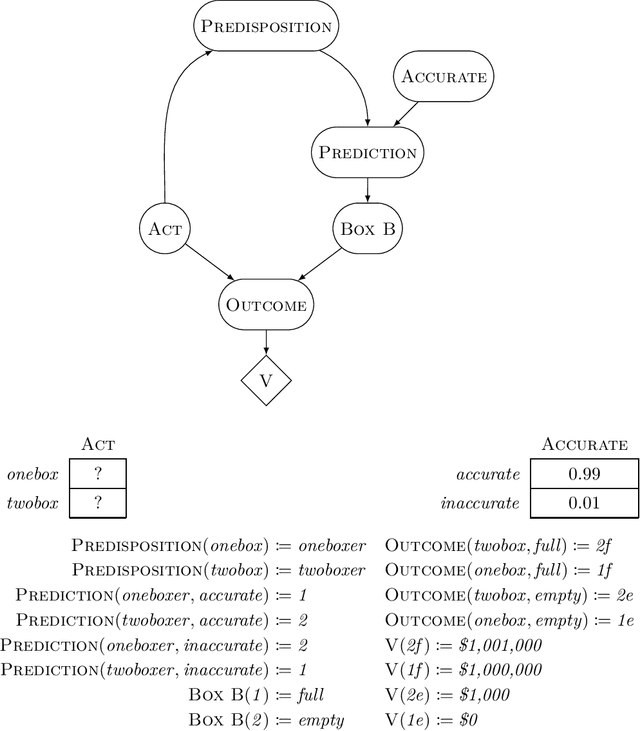
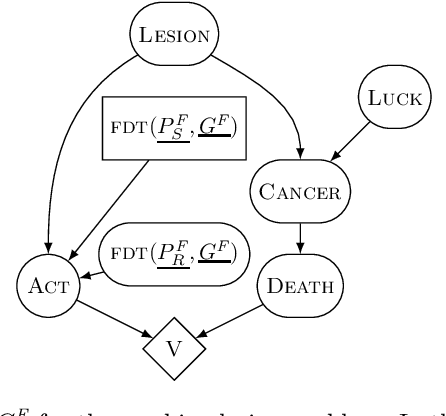

This paper describes and motivates a new decision theory known as functional decision theory (FDT), as distinct from causal decision theory and evidential decision theory. Functional decision theorists hold that the normative principle for action is to treat one's decision as the output of a fixed mathematical function that answers the question, "Which output of this very function would yield the best outcome?" Adhering to this principle delivers a number of benefits, including the ability to maximize wealth in an array of traditional decision-theoretic and game-theoretic problems where CDT and EDT perform poorly. Using one simple and coherent decision rule, functional decision theorists (for example) achieve more utility than CDT on Newcomb's problem, more utility than EDT on the smoking lesion problem, and more utility than both in Parfit's hitchhiker problem. In this paper, we define FDT, explore its prescriptions in a number of different decision problems, compare it to CDT and EDT, and give philosophical justifications for FDT as a normative theory of decision-making.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge