Clifford-Steerable Convolutional Neural Networks
Paper and Code
Feb 22, 2024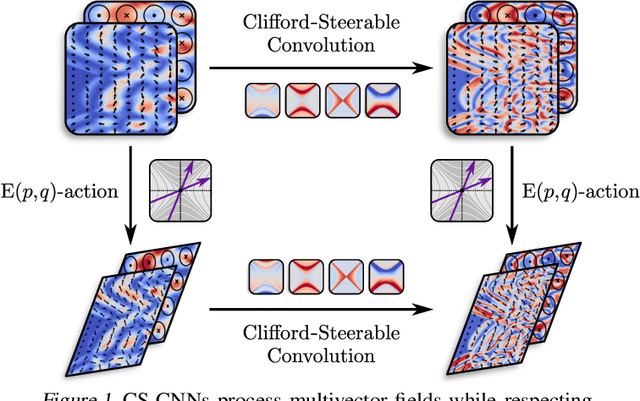
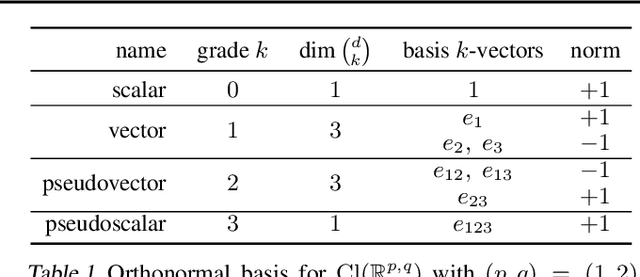
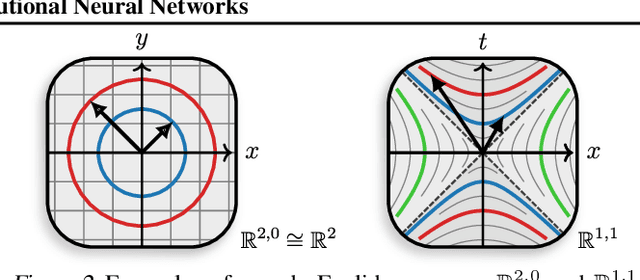
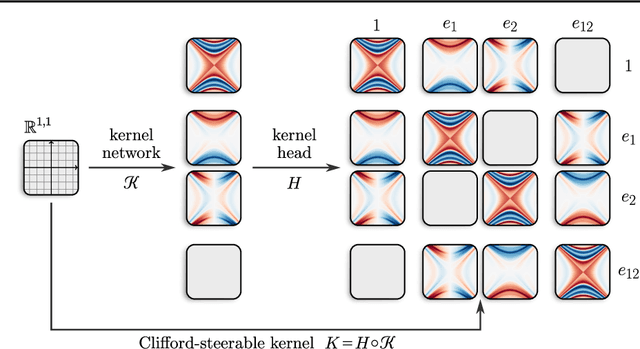
We present Clifford-Steerable Convolutional Neural Networks (CS-CNNs), a novel class of $\mathrm{E}(p, q)$-equivariant CNNs. CS-CNNs process multivector fields on pseudo-Euclidean spaces $\mathbb{R}^{p,q}$. They cover, for instance, $\mathrm{E}(3)$-equivariance on $\mathbb{R}^3$ and Poincar\'e-equivariance on Minkowski spacetime $\mathbb{R}^{1,3}$. Our approach is based on an implicit parametrization of $\mathrm{O}(p,q)$-steerable kernels via Clifford group equivariant neural networks. We significantly and consistently outperform baseline methods on fluid dynamics as well as relativistic electrodynamics forecasting tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge