Robust Multi-view Co-expression Network Inference

Unraveling the co-expression of genes across studies enhances the understanding of cellular processes. Inferring gene co-expression networks from transcriptome data presents many challenges, including spurious gene correlations, sample correlations, and batch effects. To address these complexities, we introduce a robust method for high-dimensional graph inference from multiple independent studies. We base our approach on the premise that each dataset is essentially a noisy linear mixture of gene loadings that follow a multivariate $t$-distribution with a sparse precision matrix, which is shared across studies. This allows us to show that we can identify the co-expression matrix up to a scaling factor among other model parameters. Our method employs an Expectation-Maximization procedure for parameter estimation. Empirical evaluation on synthetic and gene expression data demonstrates our method's improved ability to learn the underlying graph structure compared to baseline methods.

Causal Effect Inference with Deep Latent-Variable Models

Learning individual-level causal effects from observational data, such as inferring the most effective medication for a specific patient, is a problem of growing importance for policy makers. The most important aspect of inferring causal effects from observational data is the handling of confounders, factors that affect both an intervention and its outcome. A carefully designed observational study attempts to measure all important confounders. However, even if one does not have direct access to all confounders, there may exist noisy and uncertain measurement of proxies for confounders. We build on recent advances in latent variable modeling to simultaneously estimate the unknown latent space summarizing the confounders and the causal effect. Our method is based on Variational Autoencoders (VAE) which follow the causal structure of inference with proxies. We show our method is significantly more robust than existing methods, and matches the state-of-the-art on previous benchmarks focused on individual treatment effects.

From Ordinary Differential Equations to Structural Causal Models: the deterministic case

We show how, and under which conditions, the equilibrium states of a first-order Ordinary Differential Equation (ODE) system can be described with a deterministic Structural Causal Model (SCM). Our exposition sheds more light on the concept of causality as expressed within the framework of Structural Causal Models, especially for cyclic models.

Causal Discovery with Continuous Additive Noise Models

We consider the problem of learning causal directed acyclic graphs from an observational joint distribution. One can use these graphs to predict the outcome of interventional experiments, from which data are often not available. We show that if the observational distribution follows a structural equation model with an additive noise structure, the directed acyclic graph becomes identifiable from the distribution under mild conditions. This constitutes an interesting alternative to traditional methods that assume faithfulness and identify only the Markov equivalence class of the graph, thus leaving some edges undirected. We provide practical algorithms for finitely many samples, RESIT (Regression with Subsequent Independence Test) and two methods based on an independence score. We prove that RESIT is correct in the population setting and provide an empirical evaluation.

Cyclic Causal Discovery from Continuous Equilibrium Data

We propose a method for learning cyclic causal models from a combination of observational and interventional equilibrium data. Novel aspects of the proposed method are its ability to work with continuous data (without assuming linearity) and to deal with feedback loops. Within the context of biochemical reactions, we also propose a novel way of modeling interventions that modify the activity of compounds instead of their abundance. For computational reasons, we approximate the nonlinear causal mechanisms by (coupled) local linearizations, one for each experimental condition. We apply the method to reconstruct a cellular signaling network from the flow cytometry data measured by Sachs et al. (2005). We show that our method finds evidence in the data for feedback loops and that it gives a more accurate quantitative description of the data at comparable model complexity.

Learning Sparse Causal Models is not NP-hard

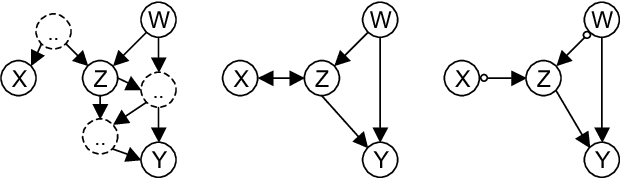
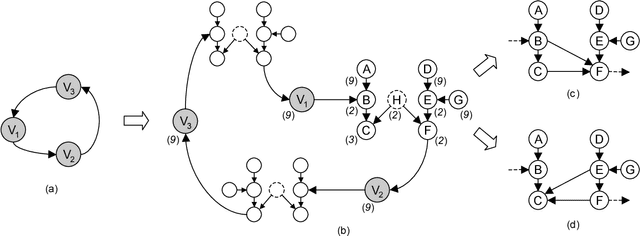
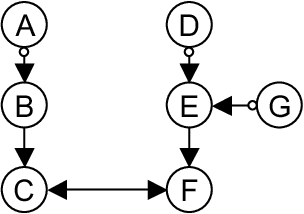
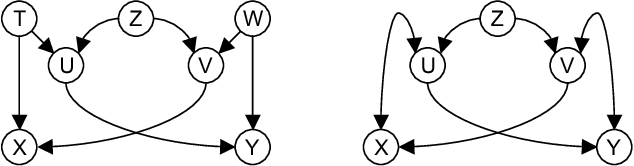
This paper shows that causal model discovery is not an NP-hard problem, in the sense that for sparse graphs bounded by node degree k the sound and complete causal model can be obtained in worst case order N^{2(k+2)} independence tests, even when latent variables and selection bias may be present. We present a modification of the well-known FCI algorithm that implements the method for an independence oracle, and suggest improvements for sample/real-world data versions. It does not contradict any known hardness results, and does not solve an NP-hard problem: it just proves that sparse causal discovery is perhaps more complicated, but not as hard as learning minimal Bayesian networks.

Sufficient conditions for convergence of Loopy Belief Propagation

We derive novel sufficient conditions for convergence of Loopy Belief Propagation (also known as the Sum-Product algorithm) to a unique fixed point. Our results improve upon previously known conditions. For binary variables with (anti-)ferromagnetic interactions, our conditions seem to be sharp.

On Causal and Anticausal Learning

We consider the problem of function estimation in the case where an underlying causal model can be inferred. This has implications for popular scenarios such as covariate shift, concept drift, transfer learning and semi-supervised learning. We argue that causal knowledge may facilitate some approaches for a given problem, and rule out others. In particular, we formulate a hypothesis for when semi-supervised learning can help, and corroborate it with empirical results.

Identifying confounders using additive noise models

We propose a method for inferring the existence of a latent common cause ('confounder') of two observed random variables. The method assumes that the two effects of the confounder are (possibly nonlinear) functions of the confounder plus independent, additive noise. We discuss under which conditions the model is identifiable (up to an arbitrary reparameterization of the confounder) from the joint distribution of the effects. We state and prove a theoretical result that provides evidence for the conjecture that the model is generically identifiable under suitable technical conditions. In addition, we propose a practical method to estimate the confounder from a finite i.i.d. sample of the effects and illustrate that the method works well on both simulated and real-world data.

Inferring deterministic causal relations

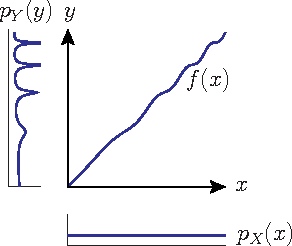
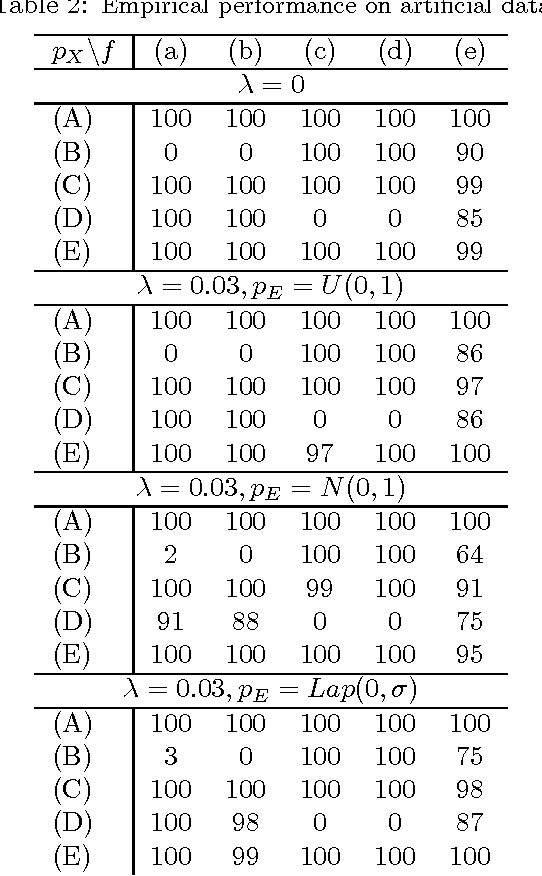
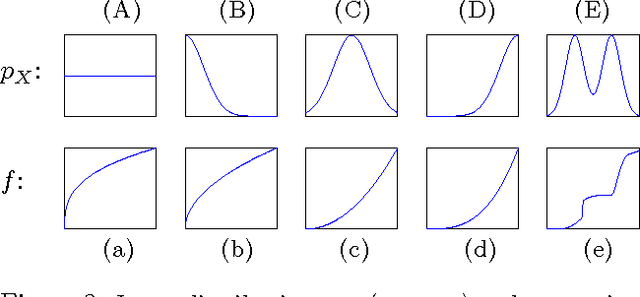
We consider two variables that are related to each other by an invertible function. While it has previously been shown that the dependence structure of the noise can provide hints to determine which of the two variables is the cause, we presently show that even in the deterministic (noise-free) case, there are asymmetries that can be exploited for causal inference. Our method is based on the idea that if the function and the probability density of the cause are chosen independently, then the distribution of the effect will, in a certain sense, depend on the function. We provide a theoretical analysis of this method, showing that it also works in the low noise regime, and link it to information geometry. We report strong empirical results on various real-world data sets from different domains.