Composite Quantile Regression With XGBoost Using the Novel Arctan Pinball Loss

This paper explores the use of XGBoost for composite quantile regression. XGBoost is a highly popular model renowned for its flexibility, efficiency, and capability to deal with missing data. The optimization uses a second order approximation of the loss function, complicating the use of loss functions with a zero or vanishing second derivative. Quantile regression -- a popular approach to obtain conditional quantiles when point estimates alone are insufficient -- unfortunately uses such a loss function, the pinball loss. Existing workarounds are typically inefficient and can result in severe quantile crossings. In this paper, we present a smooth approximation of the pinball loss, the arctan pinball loss, that is tailored to the needs of XGBoost. Specifically, contrary to other smooth approximations, the arctan pinball loss has a relatively large second derivative, which makes it more suitable to use in the second order approximation. Using this loss function enables the simultaneous prediction of multiple quantiles, which is more efficient and results in far fewer quantile crossings.

Acquiring Better Load Estimates by Combining Anomaly and Change-point Detection in Power Grid Time-series Measurements

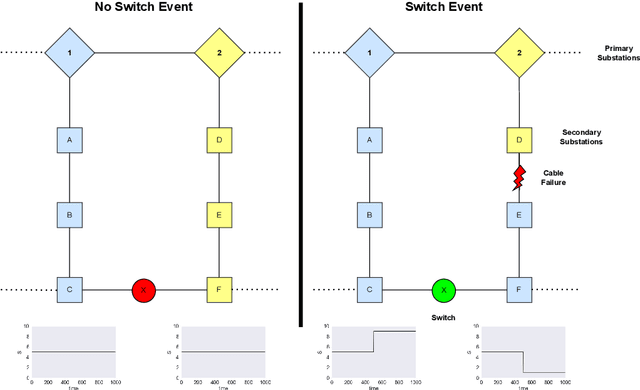
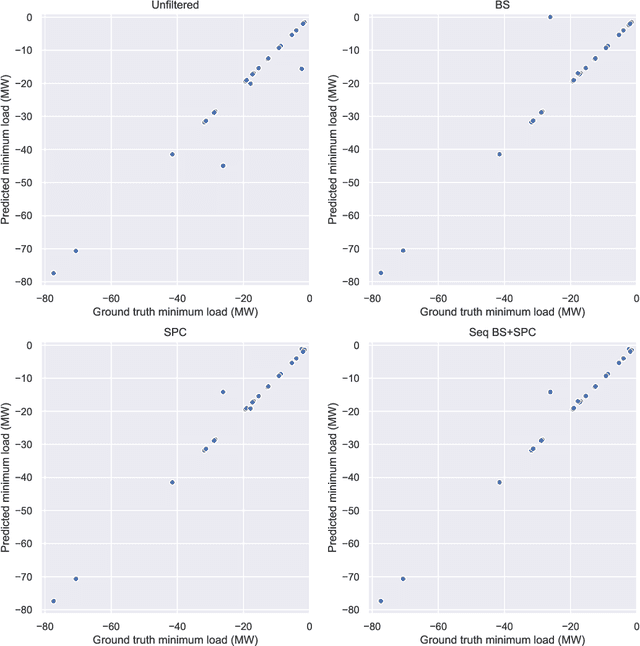
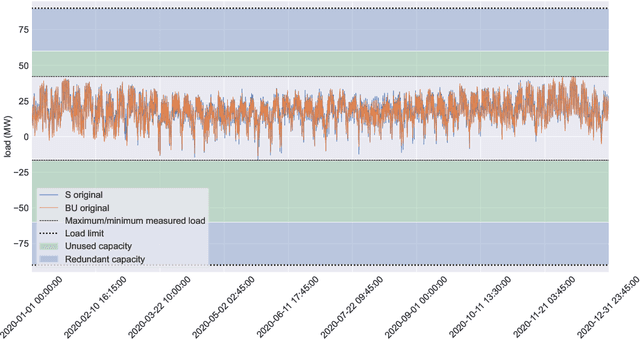
In this paper we present novel methodology for automatic anomaly and switch event filtering to improve load estimation in power grid systems. By leveraging unsupervised methods with supervised optimization, our approach prioritizes interpretability while ensuring robust and generalizable performance on unseen data. Through experimentation, a combination of binary segmentation for change point detection and statistical process control for anomaly detection emerges as the most effective strategy, specifically when ensembled in a novel sequential manner. Results indicate the clear wasted potential when filtering is not applied. The automatic load estimation is also fairly accurate, with approximately 90% of estimates falling within a 10% error margin, with only a single significant failure in both the minimum and maximum load estimates across 60 measurements in the test set. Our methodology's interpretability makes it particularly suitable for critical infrastructure planning, thereby enhancing decision-making processes.

Pfeed: Generating near real-time personalized feeds using precomputed embedding similarities

In personalized recommender systems, embeddings are often used to encode customer actions and items, and retrieval is then performed in the embedding space using approximate nearest neighbor search. However, this approach can lead to two challenges: 1) user embeddings can restrict the diversity of interests captured and 2) the need to keep them up-to-date requires an expensive, real-time infrastructure. In this paper, we propose a method that overcomes these challenges in a practical, industrial setting. The method dynamically updates customer profiles and composes a feed every two minutes, employing precomputed embeddings and their respective similarities. We tested and deployed this method to personalise promotional items at Bol, one of the largest e-commerce platforms of the Netherlands and Belgium. The method enhanced customer engagement and experience, leading to a significant 4.9% uplift in conversions.

Graph Isomorphic Networks for Assessing Reliability of the Medium-Voltage Grid

Ensuring electricity grid reliability becomes increasingly challenging with the shift towards renewable energy and declining conventional capacities. Distribution System Operators (DSOs) aim to achieve grid reliability by verifying the n-1 principle, ensuring continuous operation in case of component failure. Electricity networks' complex graph-based data holds crucial information for n-1 assessment: graph structure and data about stations/cables. Unlike traditional machine learning methods, Graph Neural Networks (GNNs) directly handle graph-structured data. This paper proposes using Graph Isomorphic Networks (GINs) for n-1 assessments in medium voltage grids. The GIN framework is designed to generalise to unseen grids and utilise graph structure and data about stations/cables. The proposed GIN approach demonstrates faster and more reliable grid assessments than a traditional mathematical optimisation approach, reducing prediction times by approximately a factor of 1000. The findings offer a promising approach to address computational challenges and enhance the reliability and efficiency of energy grid assessments.

Likelihood-ratio-based confidence intervals for neural networks

This paper introduces a first implementation of a novel likelihood-ratio-based approach for constructing confidence intervals for neural networks. Our method, called DeepLR, offers several qualitative advantages: most notably, the ability to construct asymmetric intervals that expand in regions with a limited amount of data, and the inherent incorporation of factors such as the amount of training time, network architecture, and regularization techniques. While acknowledging that the current implementation of the method is prohibitively expensive for many deep-learning applications, the high cost may already be justified in specific fields like medical predictions or astrophysics, where a reliable uncertainty estimate for a single prediction is essential. This work highlights the significant potential of a likelihood-ratio-based uncertainty estimate and establishes a promising avenue for future research.

Unsupervised anomaly detection algorithms on real-world data: how many do we need?

In this study we evaluate 32 unsupervised anomaly detection algorithms on 52 real-world multivariate tabular datasets, performing the largest comparison of unsupervised anomaly detection algorithms to date. On this collection of datasets, the $k$-thNN (distance to the $k$-nearest neighbor) algorithm significantly outperforms the most other algorithms. Visualizing and then clustering the relative performance of the considered algorithms on all datasets, we identify two clear clusters: one with ``local'' datasets, and another with ``global'' datasets. ``Local'' anomalies occupy a region with low density when compared to nearby samples, while ``global'' occupy an overall low density region in the feature space. On the local datasets the $k$NN ($k$-nearest neighbor) algorithm comes out on top. On the global datasets, the EIF (extended isolation forest) algorithm performs the best. Also taking into consideration the algorithms' computational complexity, a toolbox with these three unsupervised anomaly detection algorithms suffices for finding anomalies in this representative collection of multivariate datasets. By providing access to code and datasets, our study can be easily reproduced and extended with more algorithms and/or datasets.

Optimal Training of Mean Variance Estimation Neural Networks

This paper focusses on the optimal implementation of a Mean Variance Estimation network (MVE network) (Nix and Weigend, 1994). This type of network is often used as a building block for uncertainty estimation methods in a regression setting, for instance Concrete dropout (Gal et al., 2017) and Deep Ensembles (Lakshminarayanan et al., 2017). Specifically, an MVE network assumes that the data is produced from a normal distribution with a mean function and variance function. The MVE network outputs a mean and variance estimate and optimizes the network parameters by minimizing the negative loglikelihood. In this paper, we discuss two points: firstly, the convergence difficulties reported in recent work can be relatively easily prevented by following the recommendation from the original authors that a warm-up period should be used. During this period, only the mean is optimized assuming a fixed variance. This recommendation is often not used in practice. We experimentally demonstrate how essential this step is. We also examine if keeping the mean estimate fixed after the warm-up leads to different results than estimating both the mean and the variance simultaneously after the warm-up. We do not observe a substantial difference. Secondly, we propose a novel improvement of the MVE network: separate regularization of the mean and the variance estimate. We demonstrate, both on toy examples and on a number of benchmark UCI regression data sets, that following the original recommendations and the novel separate regularization can lead to significant improvements.

Machine Learning Meets The Herbrand Universe

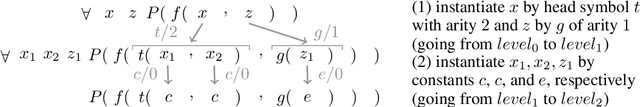
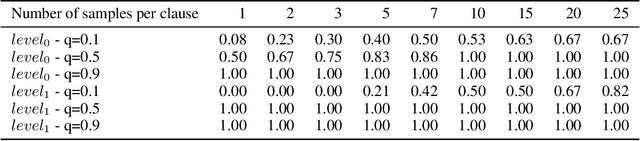
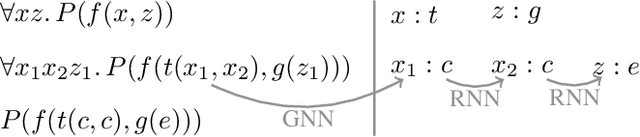
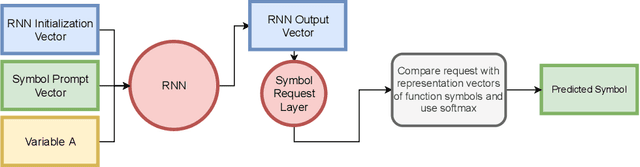
The appearance of strong CDCL-based propositional (SAT) solvers has greatly advanced several areas of automated reasoning (AR). One of the directions in AR is thus to apply SAT solvers to expressive formalisms such as first-order logic, for which large corpora of general mathematical problems exist today. This is possible due to Herbrand's theorem, which allows reduction of first-order problems to propositional problems by instantiation. The core challenge is choosing the right instances from the typically infinite Herbrand universe. In this work, we develop the first machine learning system targeting this task, addressing its combinatorial and invariance properties. In particular, we develop a GNN2RNN architecture based on an invariant graph neural network (GNN) that learns from problems and their solutions independently of symbol names (addressing the abundance of skolems), combined with a recurrent neural network (RNN) that proposes for each clause its instantiations. The architecture is then trained on a corpus of mathematical problems and their instantiation-based proofs, and its performance is evaluated in several ways. We show that the trained system achieves high accuracy in predicting the right instances, and that it is capable of solving many problems by educated guessing when combined with a ground solver. To our knowledge, this is the first convincing use of machine learning in synthesizing relevant elements from arbitrary Herbrand universes.

Automatic inference of fault tree models via multi-objective evolutionary algorithms

Fault tree analysis is a well-known technique in reliability engineering and risk assessment, which supports decision-making processes and the management of complex systems. Traditionally, fault tree (FT) models are built manually together with domain experts, considered a time-consuming process prone to human errors. With Industry 4.0, there is an increasing availability of inspection and monitoring data, making techniques that enable knowledge extraction from large data sets relevant. Thus, our goal with this work is to propose a data-driven approach to infer efficient FT structures that achieve a complete representation of the failure mechanisms contained in the failure data set without human intervention. Our algorithm, the FT-MOEA, based on multi-objective evolutionary algorithms, enables the simultaneous optimization of different relevant metrics such as the FT size, the error computed based on the failure data set and the Minimal Cut Sets. Our results show that, for six case studies from the literature, our approach successfully achieved automatic, efficient, and consistent inference of the associated FT models. We also present the results of a parametric analysis that tests our algorithm for different relevant conditions that influence its performance, as well as an overview of the data-driven methods used to automatically infer FT models.

Confident Neural Network Regression with Bootstrapped Deep Ensembles

With the rise of the popularity and usage of neural networks, trustworthy uncertainty estimation is becoming increasingly essential. In this paper we present a computationally cheap extension of Deep Ensembles for a regression setting called Bootstrapped Deep Ensembles that explicitly takes the effect of finite data into account using a modified version of the parametric bootstrap. We demonstrate through a simulation study that our method has comparable or better prediction intervals and superior confidence intervals compared to Deep Ensembles and other state-of-the-art methods. As an added bonus, our method is better capable of detecting overfitting than standard Deep Ensembles.