Composite Quantile Regression With XGBoost Using the Novel Arctan Pinball Loss

This paper explores the use of XGBoost for composite quantile regression. XGBoost is a highly popular model renowned for its flexibility, efficiency, and capability to deal with missing data. The optimization uses a second order approximation of the loss function, complicating the use of loss functions with a zero or vanishing second derivative. Quantile regression -- a popular approach to obtain conditional quantiles when point estimates alone are insufficient -- unfortunately uses such a loss function, the pinball loss. Existing workarounds are typically inefficient and can result in severe quantile crossings. In this paper, we present a smooth approximation of the pinball loss, the arctan pinball loss, that is tailored to the needs of XGBoost. Specifically, contrary to other smooth approximations, the arctan pinball loss has a relatively large second derivative, which makes it more suitable to use in the second order approximation. Using this loss function enables the simultaneous prediction of multiple quantiles, which is more efficient and results in far fewer quantile crossings.

Likelihood-ratio-based confidence intervals for neural networks

This paper introduces a first implementation of a novel likelihood-ratio-based approach for constructing confidence intervals for neural networks. Our method, called DeepLR, offers several qualitative advantages: most notably, the ability to construct asymmetric intervals that expand in regions with a limited amount of data, and the inherent incorporation of factors such as the amount of training time, network architecture, and regularization techniques. While acknowledging that the current implementation of the method is prohibitively expensive for many deep-learning applications, the high cost may already be justified in specific fields like medical predictions or astrophysics, where a reliable uncertainty estimate for a single prediction is essential. This work highlights the significant potential of a likelihood-ratio-based uncertainty estimate and establishes a promising avenue for future research.

Optimal Training of Mean Variance Estimation Neural Networks

This paper focusses on the optimal implementation of a Mean Variance Estimation network (MVE network) (Nix and Weigend, 1994). This type of network is often used as a building block for uncertainty estimation methods in a regression setting, for instance Concrete dropout (Gal et al., 2017) and Deep Ensembles (Lakshminarayanan et al., 2017). Specifically, an MVE network assumes that the data is produced from a normal distribution with a mean function and variance function. The MVE network outputs a mean and variance estimate and optimizes the network parameters by minimizing the negative loglikelihood. In this paper, we discuss two points: firstly, the convergence difficulties reported in recent work can be relatively easily prevented by following the recommendation from the original authors that a warm-up period should be used. During this period, only the mean is optimized assuming a fixed variance. This recommendation is often not used in practice. We experimentally demonstrate how essential this step is. We also examine if keeping the mean estimate fixed after the warm-up leads to different results than estimating both the mean and the variance simultaneously after the warm-up. We do not observe a substantial difference. Secondly, we propose a novel improvement of the MVE network: separate regularization of the mean and the variance estimate. We demonstrate, both on toy examples and on a number of benchmark UCI regression data sets, that following the original recommendations and the novel separate regularization can lead to significant improvements.

Scenario Parameter Generation Method and Scenario Representativeness Metric for Scenario-Based Assessment of Automated Vehicles

The development of assessment methods for the performance of Automated Vehicles (AVs) is essential to enable the deployment of automated driving technologies, due to the complex operational domain of AVs. One candidate is scenario-based assessment, in which test cases are derived from real-world road traffic scenarios obtained from driving data. Because of the high variety of the possible scenarios, using only observed scenarios for the assessment is not sufficient. Therefore, methods for generating additional scenarios are necessary. Our contribution is twofold. First, we propose a method to determine the parameters that describe the scenarios to a sufficient degree without relying on strong assumptions on the parameters that characterize the scenarios. By estimating the probability density function (pdf) of these parameters, realistic parameter values can be generated. Second, we present the Scenario Representativeness (SR) metric based on the Wasserstein distance, which quantifies to what extent the scenarios with the generated parameter values are representative of real-world scenarios while covering the actual variety found in the real-world scenarios. A comparison of our proposed method with methods relying on assumptions of the scenario parametrization and pdf estimation shows that the proposed method can automatically determine the optimal scenario parametrization and pdf estimation. Furthermore, we demonstrate that our SR metric can be used to choose the (number of) parameters that best describe a scenario. The presented method is promising, because the parameterization and pdf estimation can directly be applied to already available importance sampling strategies for accelerating the evaluation of AVs.

Confident Neural Network Regression with Bootstrapped Deep Ensembles

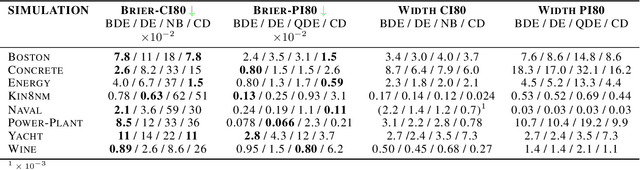
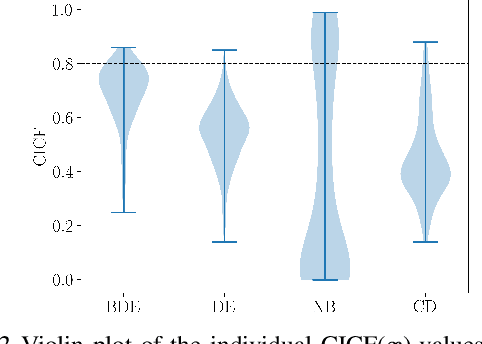
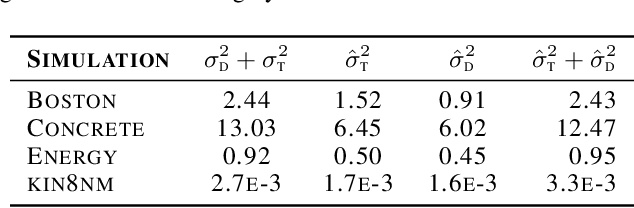
With the rise of the popularity and usage of neural networks, trustworthy uncertainty estimation is becoming increasingly essential. In this paper we present a computationally cheap extension of Deep Ensembles for a regression setting called Bootstrapped Deep Ensembles that explicitly takes the effect of finite data into account using a modified version of the parametric bootstrap. We demonstrate through a simulation study that our method has comparable or better prediction intervals and superior confidence intervals compared to Deep Ensembles and other state-of-the-art methods. As an added bonus, our method is better capable of detecting overfitting than standard Deep Ensembles.

Constrained Sampling from a Kernel Density Estimator to Generate Scenarios for the Assessment of Automated Vehicles

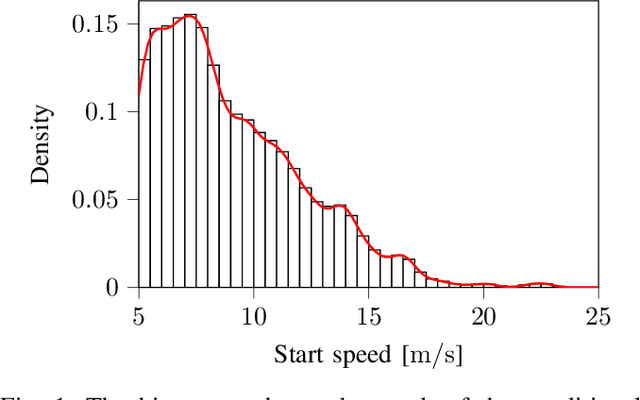
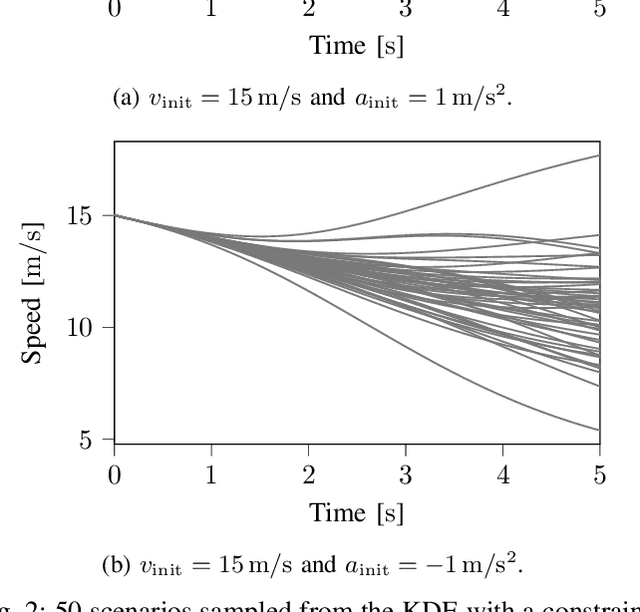
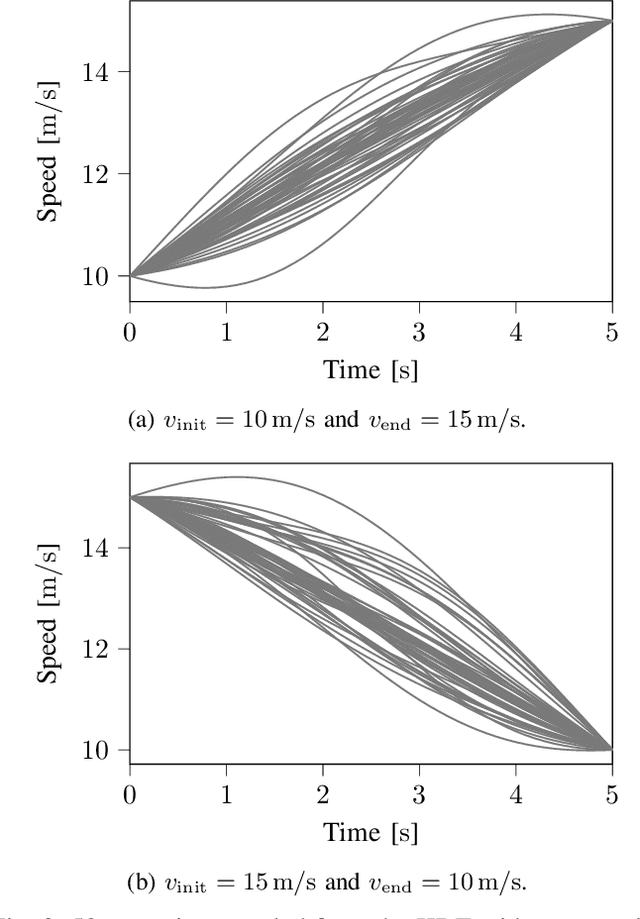
The safety assessment of automated vehicles (AVs) is an important aspect of the development cycle of AVs. A scenario-based assessment approach is accepted by many players in the field as part of the complete safety assessment. A scenario is a representation of a situation on the road to which the AV needs to respond appropriately. One way to generate the required scenario-based test descriptions is to parameterize the scenarios and to draw these parameters from a probability density function (pdf). Because the shape of the pdf is unknown beforehand, assuming a functional form of the pdf and fitting the parameters to the data may lead to inaccurate fits. As an alternative, Kernel Density Estimation (KDE) is a promising candidate for estimating the underlying pdf, because it is flexible with the underlying distribution of the parameters. Drawing random samples from a pdf estimated with KDE is possible without the need of evaluating the actual pdf, which makes it suitable for drawing random samples for, e.g., Monte Carlo methods. Sampling from a KDE while the samples satisfy a linear equality constraint, however, has not been described in the literature, as far as the authors know. In this paper, we propose a method to sample from a pdf estimated using KDE, such that the samples satisfy a linear equality constraint. We also present an algorithm of our method in pseudo-code. The method can be used to generating scenarios that have, e.g., a predetermined starting speed or to generate different types of scenarios. This paper also shows that the method for sampling scenarios can be used in case a Singular Value Decomposition (SVD) is used to reduce the dimension of the parameter vectors.

How to Evaluate Uncertainty Estimates in Machine Learning for Regression?

As neural networks become more popular, the need for accompanying uncertainty estimates increases. The current testing methodology focusses on how good the predictive uncertainty estimates explain the differences between predictions and observations in a previously unseen test set. Intuitively this is a logical approach. The current setup of benchmark data sets also allows easy comparison between the different methods. We demonstrate, however, through both theoretical arguments and simulations that this way of evaluating the quality of uncertainty estimates has serious flaws. Firstly, it cannot disentangle the aleatoric from the epistemic uncertainty. Secondly, the current methodology considers the uncertainty averaged over all test samples, implicitly averaging out overconfident and underconfident predictions. When checking if the correct fraction of test points falls inside prediction intervals, a good score on average gives no guarantee that the intervals are sensible for individual points. We demonstrate through practical examples that these effects can result in favoring a method, based on the predictive uncertainty, that has undesirable behaviour of the confidence intervals. Finally, we propose a simulation-based testing approach that addresses these problems while still allowing easy comparison between different methods.