Composite Quantile Regression With XGBoost Using the Novel Arctan Pinball Loss

This paper explores the use of XGBoost for composite quantile regression. XGBoost is a highly popular model renowned for its flexibility, efficiency, and capability to deal with missing data. The optimization uses a second order approximation of the loss function, complicating the use of loss functions with a zero or vanishing second derivative. Quantile regression -- a popular approach to obtain conditional quantiles when point estimates alone are insufficient -- unfortunately uses such a loss function, the pinball loss. Existing workarounds are typically inefficient and can result in severe quantile crossings. In this paper, we present a smooth approximation of the pinball loss, the arctan pinball loss, that is tailored to the needs of XGBoost. Specifically, contrary to other smooth approximations, the arctan pinball loss has a relatively large second derivative, which makes it more suitable to use in the second order approximation. Using this loss function enables the simultaneous prediction of multiple quantiles, which is more efficient and results in far fewer quantile crossings.

Likelihood-ratio-based confidence intervals for neural networks

This paper introduces a first implementation of a novel likelihood-ratio-based approach for constructing confidence intervals for neural networks. Our method, called DeepLR, offers several qualitative advantages: most notably, the ability to construct asymmetric intervals that expand in regions with a limited amount of data, and the inherent incorporation of factors such as the amount of training time, network architecture, and regularization techniques. While acknowledging that the current implementation of the method is prohibitively expensive for many deep-learning applications, the high cost may already be justified in specific fields like medical predictions or astrophysics, where a reliable uncertainty estimate for a single prediction is essential. This work highlights the significant potential of a likelihood-ratio-based uncertainty estimate and establishes a promising avenue for future research.

Optimal Training of Mean Variance Estimation Neural Networks

This paper focusses on the optimal implementation of a Mean Variance Estimation network (MVE network) (Nix and Weigend, 1994). This type of network is often used as a building block for uncertainty estimation methods in a regression setting, for instance Concrete dropout (Gal et al., 2017) and Deep Ensembles (Lakshminarayanan et al., 2017). Specifically, an MVE network assumes that the data is produced from a normal distribution with a mean function and variance function. The MVE network outputs a mean and variance estimate and optimizes the network parameters by minimizing the negative loglikelihood. In this paper, we discuss two points: firstly, the convergence difficulties reported in recent work can be relatively easily prevented by following the recommendation from the original authors that a warm-up period should be used. During this period, only the mean is optimized assuming a fixed variance. This recommendation is often not used in practice. We experimentally demonstrate how essential this step is. We also examine if keeping the mean estimate fixed after the warm-up leads to different results than estimating both the mean and the variance simultaneously after the warm-up. We do not observe a substantial difference. Secondly, we propose a novel improvement of the MVE network: separate regularization of the mean and the variance estimate. We demonstrate, both on toy examples and on a number of benchmark UCI regression data sets, that following the original recommendations and the novel separate regularization can lead to significant improvements.

Confident Neural Network Regression with Bootstrapped Deep Ensembles

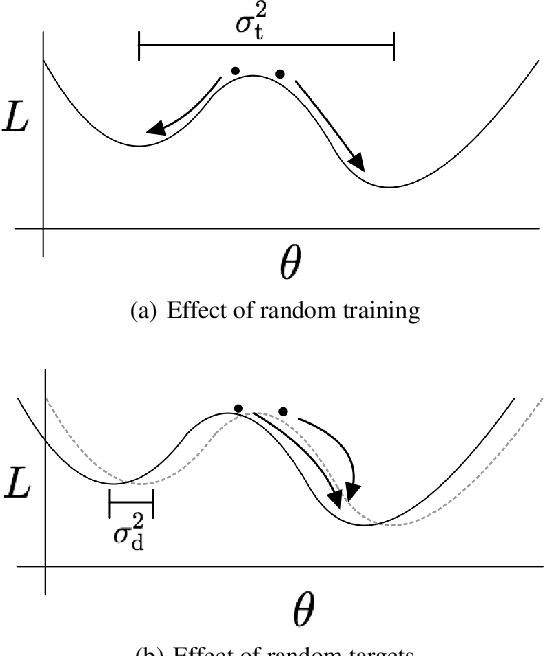
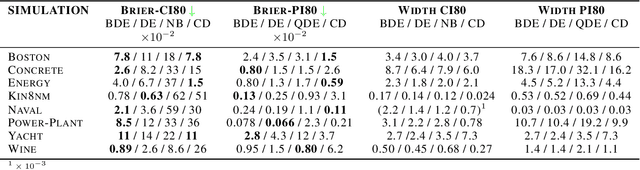
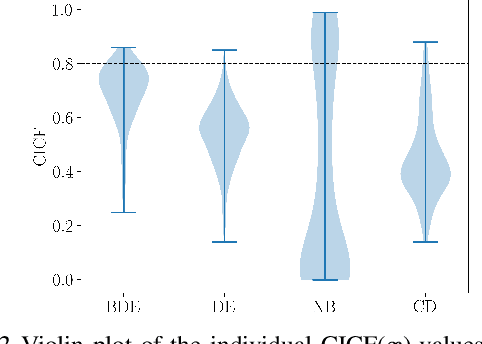
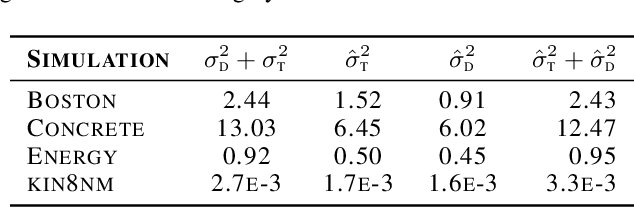
With the rise of the popularity and usage of neural networks, trustworthy uncertainty estimation is becoming increasingly essential. In this paper we present a computationally cheap extension of Deep Ensembles for a regression setting called Bootstrapped Deep Ensembles that explicitly takes the effect of finite data into account using a modified version of the parametric bootstrap. We demonstrate through a simulation study that our method has comparable or better prediction intervals and superior confidence intervals compared to Deep Ensembles and other state-of-the-art methods. As an added bonus, our method is better capable of detecting overfitting than standard Deep Ensembles.

How to Evaluate Uncertainty Estimates in Machine Learning for Regression?

As neural networks become more popular, the need for accompanying uncertainty estimates increases. The current testing methodology focusses on how good the predictive uncertainty estimates explain the differences between predictions and observations in a previously unseen test set. Intuitively this is a logical approach. The current setup of benchmark data sets also allows easy comparison between the different methods. We demonstrate, however, through both theoretical arguments and simulations that this way of evaluating the quality of uncertainty estimates has serious flaws. Firstly, it cannot disentangle the aleatoric from the epistemic uncertainty. Secondly, the current methodology considers the uncertainty averaged over all test samples, implicitly averaging out overconfident and underconfident predictions. When checking if the correct fraction of test points falls inside prediction intervals, a good score on average gives no guarantee that the intervals are sensible for individual points. We demonstrate through practical examples that these effects can result in favoring a method, based on the predictive uncertainty, that has undesirable behaviour of the confidence intervals. Finally, we propose a simulation-based testing approach that addresses these problems while still allowing easy comparison between different methods.