Nonmyopic Global Optimisation via Approximate Dynamic Programming

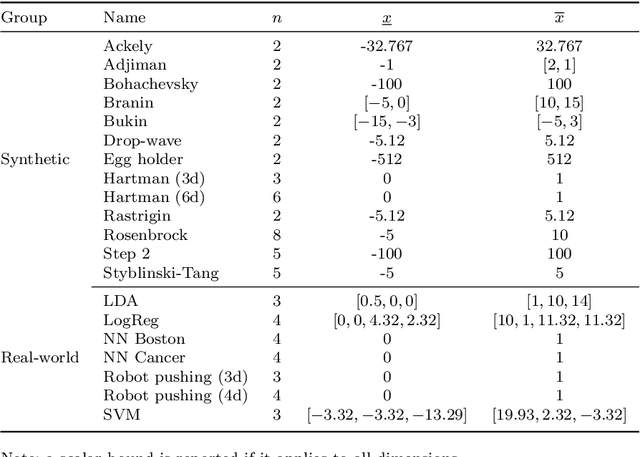
Unconstrained global optimisation aims to optimise expensive-to-evaluate black-box functions without gradient information. Bayesian optimisation, one of the most well-known techniques, typically employs Gaussian processes as surrogate models, leveraging their probabilistic nature to balance exploration and exploitation. However, Gaussian processes become computationally prohibitive in high-dimensional spaces. Recent alternatives, based on inverse distance weighting (IDW) and radial basis functions (RBFs), offer competitive, computationally lighter solutions. Despite their efficiency, both traditional global and Bayesian optimisation strategies suffer from the myopic nature of their acquisition functions, which focus solely on immediate improvement neglecting future implications of the sequential decision making process. Nonmyopic acquisition functions devised for the Bayesian setting have shown promise in improving long-term performance. Yet, their use in deterministic strategies with IDW and RBF remains unexplored. In this work, we introduce novel nonmyopic acquisition strategies tailored to IDW- and RBF-based global optimisation. Specifically, we develop dynamic programming-based paradigms, including rollout and multi-step scenario-based optimisation schemes, to enable lookahead acquisition. These methods optimise a sequence of query points over a horizon (instead of only at the next step) by predicting the evolution of the surrogate model, inherently managing the exploration-exploitation trade-off in a systematic way via optimisation techniques. The proposed approach represents a significant advance in extending nonmyopic acquisition principles, previously confined to Bayesian optimisation, to the deterministic framework. Empirical results on synthetic and hyperparameter tuning benchmark problems demonstrate that these nonmyopic methods outperform conventional myopic approaches.

Integrating Reinforcement Learning and Model Predictive Control with Applications to Microgrids

This work proposes an approach that integrates reinforcement learning and model predictive control (MPC) to efficiently solve finite-horizon optimal control problems in mixed-logical dynamical systems. Optimization-based control of such systems with discrete and continuous decision variables entails the online solution of mixed-integer quadratic or linear programs, which suffer from the curse of dimensionality. Our approach aims at mitigating this issue by effectively decoupling the decision on the discrete variables and the decision on the continuous variables. Moreover, to mitigate the combinatorial growth in the number of possible actions due to the prediction horizon, we conceive the definition of decoupled Q-functions to make the learning problem more tractable. The use of reinforcement learning reduces the online optimization problem of the MPC controller from a mixed-integer linear (quadratic) program to a linear (quadratic) program, greatly reducing the computational time. Simulation experiments for a microgrid, based on real-world data, demonstrate that the proposed method significantly reduces the online computation time of the MPC approach and that it generates policies with small optimality gaps and high feasibility rates.

Entanglement Definitions for Tethered Robots: Exploration and Analysis

In this article we consider the problem of tether entanglement for tethered robots. In many applications, such as maintenance of underwater structures, aerial inspection, and underground exploration, tethered robots are often used in place of standalone (i.e., untethered) ones. However, the presence of a tether also introduces the risk for it to get entangled with obstacles present in the environment or with itself. To avoid these situations, a non-entanglement constraint can be considered in the motion planning problem for tethered robots. This constraint can be expressed either as a set of specific tether configurations that must be avoided, or as a quantitative measure of a `level of entanglement' that can be minimized. However, the literature lacks a generally accepted definition of entanglement, with existing definitions being limited and partial. Namely, the existing entanglement definitions either require a taut tether to come into contact with an obstacle or with another tether, or they require for the tether to do a full loop around an obstacle. In practice, this means that the existing definitions do not effectively cover all instances of tether entanglement. Our goal in this article is to bridge this gap and provide new definitions of entanglement, which, together with the existing ones, can be effectively used to qualify the entanglement state of a tethered robot in diverse situations. The new definitions find application mainly in motion planning for tethered robot systems, where they can be used to obtain more safe and robust entanglement-free trajectories. The present article focuses exclusively on the presentation and analysis of the entanglement definitions. The application of the definitions to the motion planning problem is left for future work.

Reinforcement Learning with Model Predictive Control for Highway Ramp Metering

In the backdrop of an increasingly pressing need for effective urban and highway transportation systems, this work explores the synergy between model-based and learning-based strategies to enhance traffic flow management by use of an innovative approach to the problem of highway ramp metering control that embeds Reinforcement Learning techniques within the Model Predictive Control framework. The control problem is formulated as an RL task by crafting a suitable stage cost function that is representative of the traffic conditions, variability in the control action, and violations of a safety-critical constraint on the maximum number of vehicles in queue. An MPC-based RL approach, which merges the advantages of the two paradigms in order to overcome the shortcomings of each framework, is proposed to learn to efficiently control an on-ramp and to satisfy its constraints despite uncertainties in the system model and variable demands. Finally, simulations are performed on a benchmark from the literature consisting of a small-scale highway network. Results show that, starting from an MPC controller that has an imprecise model and is poorly tuned, the proposed methodology is able to effectively learn to improve the control policy such that congestion in the network is reduced and constraints are satisfied, yielding an improved performance compared to the initial controller.

Regret Analysis of Learning-Based Linear Quadratic Gaussian Control with Additive Exploration

In this paper, we analyze the regret incurred by a computationally efficient exploration strategy, known as naive exploration, for controlling unknown partially observable systems within the Linear Quadratic Gaussian (LQG) framework. We introduce a two-phase control algorithm called LQG-NAIVE, which involves an initial phase of injecting Gaussian input signals to obtain a system model, followed by a second phase of an interplay between naive exploration and control in an episodic fashion. We show that LQG-NAIVE achieves a regret growth rate of $\tilde{\mathcal{O}}(\sqrt{T})$, i.e., $\mathcal{O}(\sqrt{T})$ up to logarithmic factors after $T$ time steps, and we validate its performance through numerical simulations. Additionally, we propose LQG-IF2E, which extends the exploration signal to a `closed-loop' setting by incorporating the Fisher Information Matrix (FIM). We provide compelling numerical evidence of the competitive performance of LQG-IF2E compared to LQG-NAIVE.

PRISMA: A Novel Approach for Deriving Probabilistic Surrogate Safety Measures for Risk Evaluation

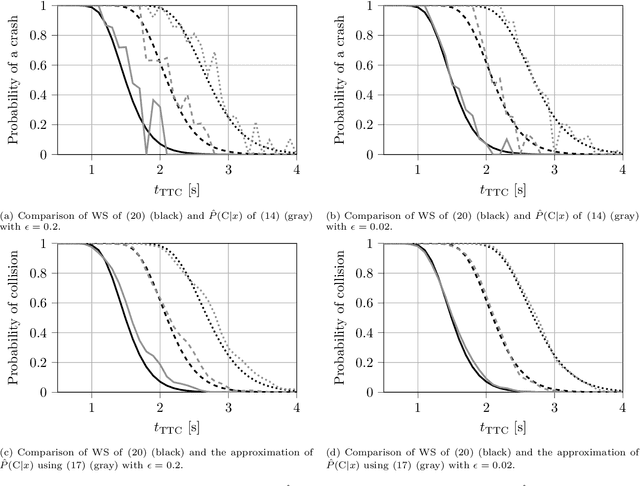
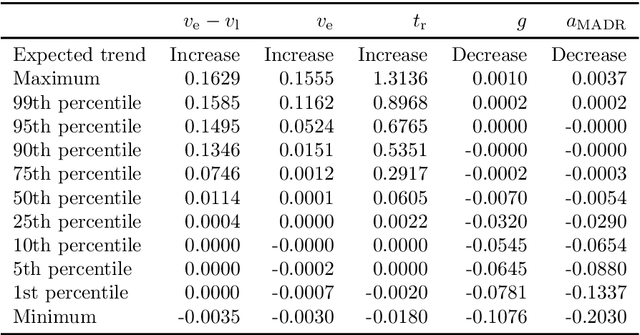
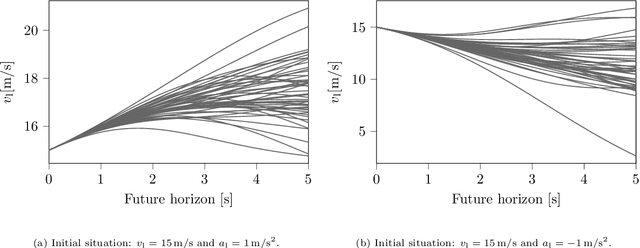
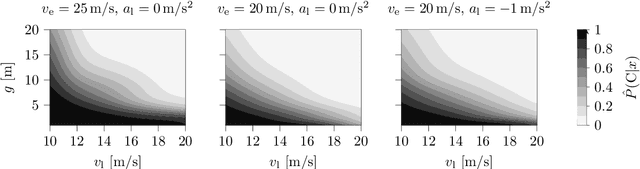
Surrogate Safety Measures (SSMs) are used to express road safety in terms of the safety risk in traffic conflicts. Typically, SSMs rely on assumptions regarding the future evolution of traffic participant trajectories to generate a measure of risk. As a result, they are only applicable in scenarios where those assumptions hold. To address this issue, we present a novel data-driven Probabilistic RISk Measure derivAtion (PRISMA) method. The PRISMA method is used to derive SSMs that can be used to calculate in real time the probability of a specific event (e.g., a crash). Because we adopt a data-driven approach to predict the possible future evolutions of traffic participant trajectories, less assumptions on these trajectories are needed. Since the PRISMA is not bound to specific assumptions, multiple SSMs for different types of scenarios can be derived. To calculate the probability of the specific event, the PRISMA method uses Monte Carlo simulations to estimate the occurrence probability of the specified event. We further introduce a statistical method that requires fewer simulations to estimate this probability. Combined with a regression model, this enables our derived SSMs to make real-time risk estimations. To illustrate the PRISMA method, an SSM is derived for risk evaluation during longitudinal traffic interactions. It is very difficult, if not impossible, to objectively compare the relative merits of two SSMs. Instead, we provide a method for benchmarking our derived SSM with respect to expected risk trends. The application of the benchmarking illustrates that the SSM matches the expected risk trends. Whereas the derived SSM shows the potential of the PRISMA method, future work involves applying the approach for other types of traffic conflicts, such as lateral traffic conflicts or interactions with vulnerable road users.

Suboptimality analysis of receding horizon quadratic control with unknown linear systems and its applications in learning-based control

For a receding-horizon controller with a known system and with an approximate terminal value function, it is well-known that increasing the prediction horizon can improve its control performance. However, when the prediction model is inexact, a larger prediction horizon also causes propagation and accumulation of the prediction error. In this work, we aim to analyze the effect of the above trade-off between the modeling error, the terminal value function error, and the prediction horizon on the performance of a nominal receding-horizon linear quadratic (LQ) controller. By developing a novel perturbation result of the Riccati difference equation, a performance upper bound is obtained and suggests that for many cases, the prediction horizon should be either 1 or infinity to improve the control performance, depending on the relative difference between the modeling error and the terminal value function error. The obtained suboptimality performance bound is also applied to provide end-to-end performance guarantees, e.g., regret bounds, for nominal receding-horizon LQ controllers in a learning-based setting.

Finite-sample analysis of identification of switched linear systems with arbitrary or restricted switching

This work aims to derive a data-independent finite-sample error bound for the least-squares (LS) estimation error of switched linear systems when the state and the switching signal are measured. While the existing finite-sample bounds for linear system identification extend to the problem under consideration, the Gramian of the switched system, an essential term in the error bound, depends on the measured switching signal. Therefore, data-independent bounds on the spectrum of the Gramian are developed for globally asymptotically and marginally stable switched systems when the switching is arbitrary or subject to an average dwell time constraint. Combining the bounds on the spectrum of the Gramian and the preliminary error bound extended from linear system identification leads to the error bound for the LS estimate of the switched system.

Scenario Parameter Generation Method and Scenario Representativeness Metric for Scenario-Based Assessment of Automated Vehicles

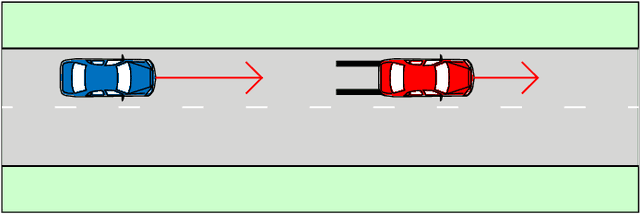
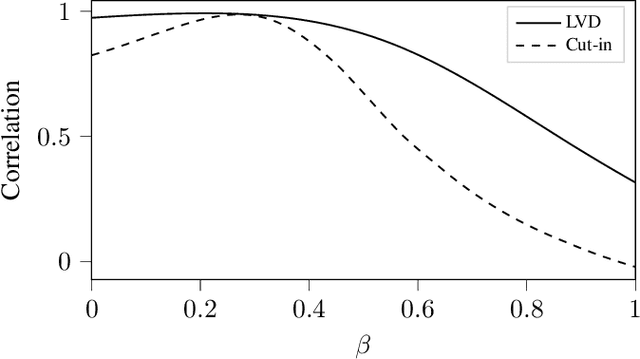
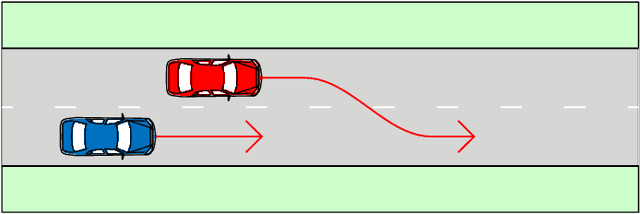
The development of assessment methods for the performance of Automated Vehicles (AVs) is essential to enable the deployment of automated driving technologies, due to the complex operational domain of AVs. One candidate is scenario-based assessment, in which test cases are derived from real-world road traffic scenarios obtained from driving data. Because of the high variety of the possible scenarios, using only observed scenarios for the assessment is not sufficient. Therefore, methods for generating additional scenarios are necessary. Our contribution is twofold. First, we propose a method to determine the parameters that describe the scenarios to a sufficient degree without relying on strong assumptions on the parameters that characterize the scenarios. By estimating the probability density function (pdf) of these parameters, realistic parameter values can be generated. Second, we present the Scenario Representativeness (SR) metric based on the Wasserstein distance, which quantifies to what extent the scenarios with the generated parameter values are representative of real-world scenarios while covering the actual variety found in the real-world scenarios. A comparison of our proposed method with methods relying on assumptions of the scenario parametrization and pdf estimation shows that the proposed method can automatically determine the optimal scenario parametrization and pdf estimation. Furthermore, we demonstrate that our SR metric can be used to choose the (number of) parameters that best describe a scenario. The presented method is promising, because the parameterization and pdf estimation can directly be applied to already available importance sampling strategies for accelerating the evaluation of AVs.

Constrained Sampling from a Kernel Density Estimator to Generate Scenarios for the Assessment of Automated Vehicles

The safety assessment of automated vehicles (AVs) is an important aspect of the development cycle of AVs. A scenario-based assessment approach is accepted by many players in the field as part of the complete safety assessment. A scenario is a representation of a situation on the road to which the AV needs to respond appropriately. One way to generate the required scenario-based test descriptions is to parameterize the scenarios and to draw these parameters from a probability density function (pdf). Because the shape of the pdf is unknown beforehand, assuming a functional form of the pdf and fitting the parameters to the data may lead to inaccurate fits. As an alternative, Kernel Density Estimation (KDE) is a promising candidate for estimating the underlying pdf, because it is flexible with the underlying distribution of the parameters. Drawing random samples from a pdf estimated with KDE is possible without the need of evaluating the actual pdf, which makes it suitable for drawing random samples for, e.g., Monte Carlo methods. Sampling from a KDE while the samples satisfy a linear equality constraint, however, has not been described in the literature, as far as the authors know. In this paper, we propose a method to sample from a pdf estimated using KDE, such that the samples satisfy a linear equality constraint. We also present an algorithm of our method in pseudo-code. The method can be used to generating scenarios that have, e.g., a predetermined starting speed or to generate different types of scenarios. This paper also shows that the method for sampling scenarios can be used in case a Singular Value Decomposition (SVD) is used to reduce the dimension of the parameter vectors.