Fast Collision Probability Estimation for Automated Driving using Multi-circular Shape Approximations

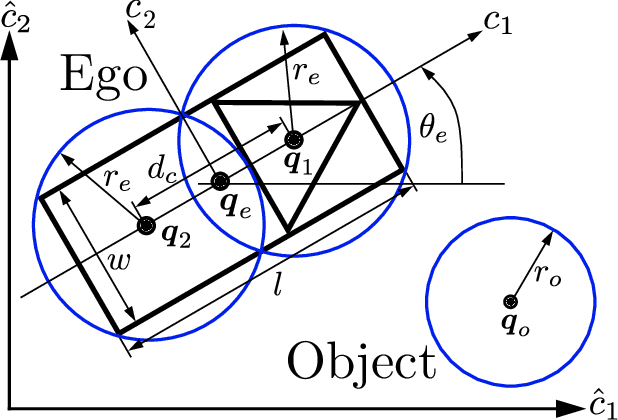
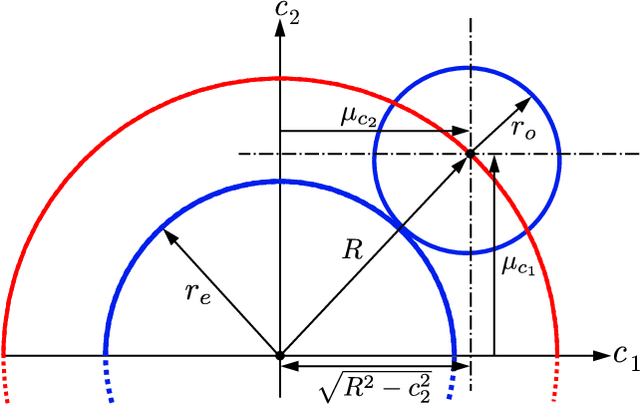
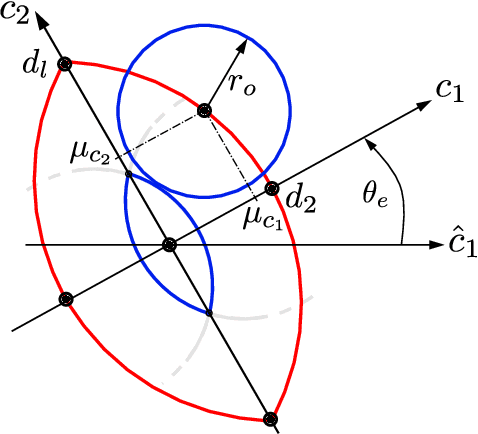
Many state-of-the-art methods for safety assessment and motion planning for automated driving require estimation of the probability of collision (POC). To estimate the POC, a shape approximation of the colliding actors and probability density functions of the associated uncertain kinematic variables are required. Even with such information available, the derivation of the POC is in general, i.e., for any shape and density, only possible with Monte Carlo sampling (MCS). Random sampling of the POC, however, is challenging as computational resources are limited in real-world applications. We present expressions for the POC in the presence of Gaussian uncertainties, based on multi-circular shape approximations. In addition, we show that the proposed approach is computationally more efficient than MCS. Lastly, we provide a method for upper and lower bounding the estimation error for the POC induced by the used shape approximations.

A New Safety Objective for the Calibration of the Intelligent Driver Model

The intelligent driver model (IDM) is one of the most widely used car-following (CF) models in recent years. The parameters of this model have been calibrated using real trajectories obtained from naturalistic driving ,driving simulator experiment and drone data. An important aspect of the model calibration process is defining the main objective of the calibration. This objective, influences the objective function and the performance measure for the calibration. For example, to calibrate CF models, the objective is usually to minimize the error in measured spacing or speed while important safety aspects of the models such as the collision avoidance mechanisms are ignored. For such models, there is no guarantee that the calibrated parameters will preserve the safety properties of the model since they are not explicitly taken into account. To explicitly account for the safety properties during calibration, this paper proposes a simple objective function which minimizes both the error in the actual measured spacing (as it is currently done) and the error in the dynamic safety spacing (desired minimum gap) derived from the collision free property of the IDM model. The proposed objective function is used to calibrate two variants of the IDM using vehicle trajectories obtained with drone from a Dutch highway. The calibration performance is then compared in terms of the error in actual spacing and time gap. The results show that the proposed safety objective 15 function leads to lower errors in spacing and time gap compared to when minimizing for only spacing and preserves collision property of the IDM.

PRISMA: A Novel Approach for Deriving Probabilistic Surrogate Safety Measures for Risk Evaluation

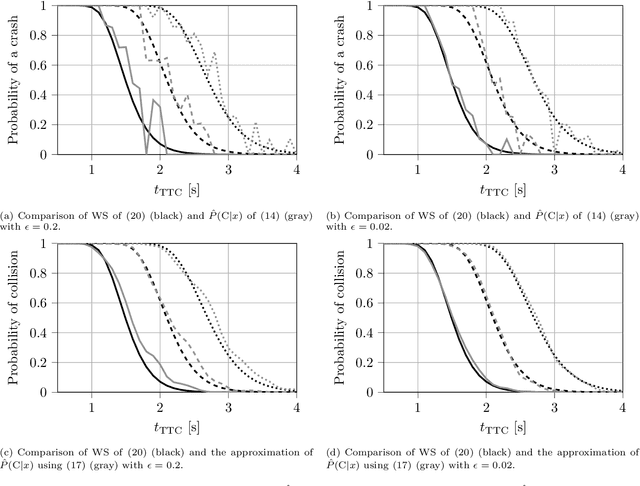
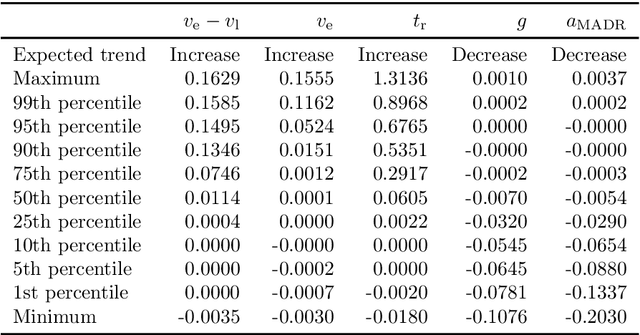
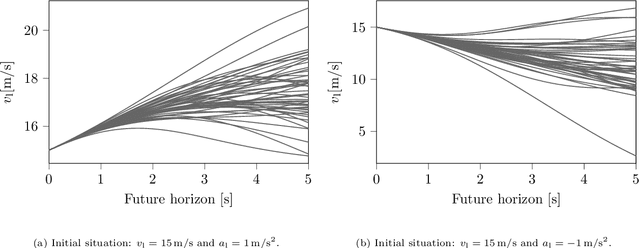
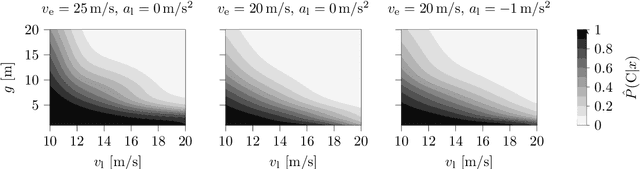
Surrogate Safety Measures (SSMs) are used to express road safety in terms of the safety risk in traffic conflicts. Typically, SSMs rely on assumptions regarding the future evolution of traffic participant trajectories to generate a measure of risk. As a result, they are only applicable in scenarios where those assumptions hold. To address this issue, we present a novel data-driven Probabilistic RISk Measure derivAtion (PRISMA) method. The PRISMA method is used to derive SSMs that can be used to calculate in real time the probability of a specific event (e.g., a crash). Because we adopt a data-driven approach to predict the possible future evolutions of traffic participant trajectories, less assumptions on these trajectories are needed. Since the PRISMA is not bound to specific assumptions, multiple SSMs for different types of scenarios can be derived. To calculate the probability of the specific event, the PRISMA method uses Monte Carlo simulations to estimate the occurrence probability of the specified event. We further introduce a statistical method that requires fewer simulations to estimate this probability. Combined with a regression model, this enables our derived SSMs to make real-time risk estimations. To illustrate the PRISMA method, an SSM is derived for risk evaluation during longitudinal traffic interactions. It is very difficult, if not impossible, to objectively compare the relative merits of two SSMs. Instead, we provide a method for benchmarking our derived SSM with respect to expected risk trends. The application of the benchmarking illustrates that the SSM matches the expected risk trends. Whereas the derived SSM shows the potential of the PRISMA method, future work involves applying the approach for other types of traffic conflicts, such as lateral traffic conflicts or interactions with vulnerable road users.